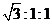
知识点：10.空间角与距离

B

解：如图，在侧面PAB内，作AM⊥PB，垂足为M。连结CM、AC，则∠AMC为二面角A−PB−C的平面角。不妨设AB=2，则，斜高为，故，由此得。在△AMC中，由余弦定理得。

知识点：3.不等式选讲

A

解：令，则有，排除B、D。由对称性排除C，从而只有A正确。

一般地，对k∈R，令，则原不等式为，由此易知原不等式等价于，对任意的k∈R成立。由于

，

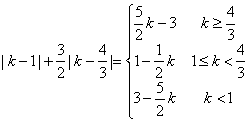所以，从而上述不等式等价于。

知识点：2.古典概型

D

解：甲、乙二人每人摸出一个小球都有9种不同的结果，故基本事件总数为9²=81个。由不等式a−2b+10>0得2b<a+10，于是，当b=1、2、3、4、5时，每种情形a可取1、2、…、9中每一个值，使不等式成立，则共有9×5=45种；当b=6时，a可取3、4、…、9中每一个值，有7种；当b=7时，a可取5、6、7、8、9中每一个值，有5种；当b=8时，a可取7、8、9中每一个值，有3种；当b=9时，a只能取9，有1种。于是，所求事件的概率为。

知识点：9.正弦定理和余弦定理（解三角形）

C

解：令c=π，则对任意的x∈R，都有f(x)+f(x−c)=2，于是取，c=π，则对任意的x∈R，af(x)+bf(x−c)=1，由此得。

一般地，由题设可得，，其中且，于是af(x)+bf(x−c)=1可化为

，即

，所以

。

由已知条件，上式对任意x∈R恒成立，故必有，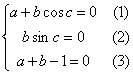

若b=0，则由(1)知a=0，显然不满足(3)式，故b≠0。所以，由(2)知sinc=0，故c=2kπ+π或c=2kπ(k∈Z)。当c=2kπ时，cosc=1，则(1)、(3)两式矛盾。故c=2kπ+π(k∈Z)，cosc=−1。由(1)、(3)知，所以。

知识点：2.双曲线

A

解：设圆O₁和圆O₂的半径分别是r₁、r₂，|O₁O₂|=2c，则一般地，圆P的圆心轨迹是焦点为O₁、O₂，且离心率分别是和的圆锥曲线（当r₁=r₂时，O₁O₂的中垂线是轨迹的一部份，当c=0时，轨迹是两个同心圆）。

当r₁=r₂且r₁+r₂<2c时，圆P的圆心轨迹如选项B；当0<2c<|r₁−r₂|时，圆P的圆心轨迹如选项C；当r₁≠r₂且r₁+r₂<2c时，圆P的圆心轨迹如选项D。由于选项A中的椭圆和双曲线的焦点不重合，因此圆P的圆心轨迹不可能是选项A。

知识点：3.集合的基本运算

B

解：先证|A∪B|≤66，只须证|A|≤33，为此只须证若A是{1，2，…，49}的任一个34元子集，则必存在n∈A，使得2n+2∈B。证明如下：

将{1，2，…，49}分成如下33个集合：{1，4}，{3，8}，{5，12}，…，{23，48}共12个；{2，6}，{10，22}，{14，30}，{18，38}共4个；{25}，{27}，{29}，…，{49}共13个；{26}，{34}，{42}，{46}共4个。由于A是{1，2，…，49}的34元子集，从而由抽屉原理可知上述33个集合中至少有一个2元集合中的数均属于A，即存在n∈A，使得2n+2∈B。

如取A={1，3，5，…，23，2，10，14，18，25，27，29，…，49，26，34，42，46}，

B={2n+2|n∈A}，则A、B满足题设且|A∪B|≤66。

知识点：3.平面向量的基本定理及其坐标表示

解：如图，设AC与BD交于F点，则|PA|+|PC|≥|AC|=|FA|+|FC|，|PB|+|PD|≥|BD|=|FB|+|FD|，因此，当动点P与F点重合时，|PA|+|PB|+|PC|+|PD|取到最小值。

知识点：4.平面向量的数量积（夹角、模）

解：因为，所以，即。因为，

，，所以，即。设与的夹角为θ，则有，即3cosθ=2，所以。

知识点：3.空间几何体的表面积与体积

解：如图，球面与正方体的六个面都相交，所得的交线分为两类：一类在顶点A所在的三个面上，即面AA₁B₁B、面ABCD和面AA₁D₁D上；另一类在不过顶点A的三个面上，即面BB₁C₁C、面CC₁D₁D和面A₁B₁C₁D₁上。在面AA₁B₁B上，交线为弧EF且在过球心A的大圆上，因为，AA₁=1，则。同理，所以，故弧EF的长为，而这样的弧共有三条。在面BB₁C₁C上，交线为弧FG且在距球心为1的平面与球面相交所得的小圆上，此时，小圆的圆心为B，半径为，，所以弧FG的长为。这样的弧也有三条。

于是，所得的曲线长为。

知识点：4.等比数列及其性质

解：因为，故由已知条件知道：1+q+q²为，其中m为正整数。令，则

。由于q是小于1的正有理数，所以，即5≤m≤13且是某个有理数的平方，由此可知。

知识点：5.三角函数的求值、化简与证明

解：实际上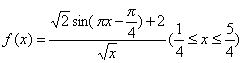，设，则g(x)≥0，g(x)在上是增函数，在上是减函数，且y=g(x)的图像关于直线对称，则对任意，存在，使g(x₂)=g(x₁)。于是

，而f(x)在上是减函数，所以，即f(x)在上的最小值是。

知识点：1.两个计数原理

3960

解：使2个a既不同行也不同列的填法有C₄²A₄²=72种，同样，使2个b既不同行也不同列的填法也有C₄²A₄²=72种，故由乘法原理，这样的填法共有72²种，其中不符合要求的有两种情况：2个a所在的方格内都填有b的情况有72种；2个a所在的方格内仅有1个方格内填有b的情况有C₁₆¹A₉²=16×72种。所以，符合题设条件的填法共有72²−72−16×72=3960种。

知识点：8.数学归纳法

证明：由于，因此，于是，对任意的正整数n≥2，有

，即a_n+1<a_n。

知识点：3.导数在研究函数中的应用

解：设点M、N的坐标分别为(x₁，y₁)和(x₂，y₂)，曲线C在点M、N处的切线分别为l₁、l₂，其交点P的坐标为(x_p，y_p)。若直线l的斜率为k，则l的方程为y=kx+1。

由方程组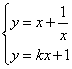，消去y，得，即(k−1)x²+x−1=0。由题意知，该方程在(0，+∞)上有两个相异的实根x₁、x₂，故k≠1，且Δ=1+4(k−1)>0…(1)，…(2)，…(3)，由此解得。对求导，得，则，，于是直线l₁的方程为，即，化简后得到直线l₁的方程为…(4)。同理可求得直线l₂的方程为…(5)。(4)−(5)得，因为x₁≠x₂，故有…(6)。将(2)(3)两式代入(6)式得x_p=2。(4)+(5)得…(7)，其中，，代入(7)式得2y_p=(3−2k)x_p+2，而x_p=2，得y_p=4−2k。又由得，即点P的轨迹为(2，2)，(2，2.5)两点间的线段（不含端点）。

知识点：5.奇偶性与周期性

证明：记，，则f(x)=g(x)+h(x)，且g(x)是偶函数，h(x)是奇函数，对任意的x∈R，g(x+2π)=g(x)，h(x+2π)=h(x)。令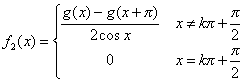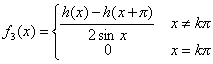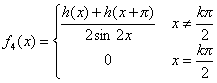，，，，其中k为任意整数。

容易验证f_i(x)，i=1，2，3，4是偶函数，且对任意的x∈R，f_i(x+π)=f_i(x)，i=1，2，3，4。下证对任意的x∈R，有f₁(x)+f₂(x)cosx=g(x)。当时，显然成立；当时，因为，而

，故对任意的x∈R，f₁(x)+f₂(x)cosx=g(x)。

下证对任意的x∈R，有f₃(x)sinx+f₄(x)sin2x=h(x)。当时，显然成立；当x=kπ时，h(x)=h(kπ)=h(kπ−2kπ)=h(−kπ)=−h(kπ)，所以h(x)=h(kπ)=0，而此时f₃(x)sinx+f₄(x)sin2x=0，故h(x)=f₃(x)sinx+f₄(x)sin2x；当时，

，故，又f₄(x)sin2x=0，从而有h(x)=f₃(x)sinx+f₄(x)sin2x。

于是，对任意的x∈R，有f₃(x)sinx+f₄(x)sin2x=h(x)。综上所述，结论得证。