知识点：4.互斥事件及其发生的概率

D

【考点】互斥事件与对立事件．

【专题】概率与统计．

【分析】列举每个事件所包含的基本事件，结合互斥事件和对立事件的定义，依次验证即可

【解答】解：对于A：事件：“至少有一个红球”与事件：“都是黑球”，这两个事件是对立事件，∴A不正确

对于B：事件：“至少有一个黑球”与事件：“都是黑球”可以同时发生，如：一个红球一个黑球，∴B不正确

对于C：事件：“至少有一个黑球”与事件：“至少有1个红球”可以同时发生，如：一个红球一个黑球，∴C不正确

对于D：事件：“恰有一个黑球”与“恰有2个黑球”不能同时发生，∴这两个事件是互斥事件，

又由从装有2个红球和2个黑球的口袋内任取2个球，

得到所有事件为“恰有1个黑球”与“恰有2个黑球”以及“恰有2个红球”三种情况，故这两个事件是不是对立事件，

∴D正确

故选D

【点评】本题考查互斥事件与对立事件．首先要求理解互斥事件和对立事件的定义，理解互斥事件与对立事件的联系与区别．同时要能够准确列举某一事件所包含的基本事件．属简单题

知识点：1.随机事件的概率

B

【考点】等可能事件的概率．

【专题】概率与统计．

【分析】求得甲获胜的概率为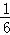，可得表示甲没有获胜的概率，即乙不输的概率．

【解答】解：由题意可得，甲获胜的概率为1﹣﹣=，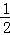

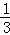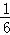而1﹣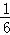=，故表示甲没有获胜的概率，即乙不输的概率，

故选B．

【点评】本题主要考查等可能事件的概率，事件和它的对立事件概率间的关系，属于中档题．

知识点：2.用样本估计总体

B

【考点】简单随机抽样．

【专题】计算题；整体思想；定义法；概率与统计．

【分析】分别根据相应的定义判断即可．

【解答】解：对于A，相同数据需要重复记录；故错误，

对于B．系统抽样在第一段抽样时一般采用简单随机抽样，故正确，

对于C，事件A与事件B的和事件是指该事件发生当且仅当事件A或事件B发生，故错误，

对于D，分层抽样是一种等可能抽样，故错误

故选B．

【点评】本题考查了茎叶图和系统抽样分层抽样以及互斥事件的概率的问题，属于基础题．

知识点：1.随机抽样

C

【考点】简单随机抽样．

【专题】计算题；整体思想；定义法；概率与统计．

【分析】如果总体和样本容量都很大时，采用随机抽样会很麻烦，就可以使用系统抽样；如果总体是具有明显差异的几个部分组成的，则采用分层抽样；从包含有N个个体的总体中抽取样本量为n个样本，总体和样本容量都不大时，采用随机抽样．

【解答】解：总体容量较小，用抽签法；总体由差异明显的两个层次组成，需选用分层抽样；总体容量较大，样本容量较小，宜用随机数法；总体容量较大，样本容量也较大，宜用系统抽样，

故选C．

【点评】本题考查收集数据的方法，考查系统抽样，分层抽样，简单随机抽样的合理运用，是基础题．解题时要认真审题，仔细解答．

知识点：2.古典概型

D

【考点】古典概型及其概率计算公式．

【专题】应用题；整体思想；定义法；概率与统计．

【分析】根据古典概型的特征：有限性和等可能性进行排除即可．

【解答】解：A、B两项中的基本事件的发生不是等可能的；C项中基本事件的个数是无限多个；D项中基本事件的发生是等可能的，且是有限个．

故选：D．

【点评】本题考查古典概型的判断，是基础题，解题时要认真审题，注意古典概型的两个特征：有限性和等可能性的合理运用．

知识点：13.函数与方程

C

【考点】函数零点的判定定理．

【专题】函数的性质及应用．

【分析】可得f（2）=2＞0，f（4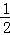）=﹣＜0，由零点的判定定理可得．

【解答】解：∵f（x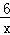）=﹣log2x，

∴f（2）=2＞0，f（4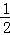）=﹣＜0，

满足f（2）f（4）＜0，

∴f（x）在区间（2，4）内必有零点，

故选：C

【点评】本题考查还是零点的判断，属基础题．

知识点：2.用样本估计总体

C

【考点】用样本的频率分布估计总体分布；众数、中位数、平均数．

【专题】概率与统计．

【分析】由于在频率分布直方图中，中位数使得直方图左右两侧频率相等，故中位数右侧的频率为0.50．由残缺的频率分布直方图可求[35，45）段上的频率是0.40＜0.50，[30，45）岁之间频率是0.75＞0.50，可知中位数在区间[30，35）内，再根据频率即可求出中位数．

【解答】解：由图知，抽到的司机年龄都在[30，35）岁之间频率是0.35；

抽到的司机年龄都在[35，40）岁之间频率是0.30；

抽到的司机年龄都在[40，45）岁之间频率是0.10．

由于在频率分布直方图中，中位数使得左右频率相等，故中位数右侧的频率为0.50．

而[35，45）段上的频率是0.40＜0.50，[30，45）岁之间频率是0.75＞0.50；

故中位数在区间[30，35）内，还要使其右侧且在[30，35）岁之间频率是0.10，

所以中位数是35﹣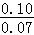≈33.6．

故答案选C．

【点评】本题考查了由频率分布直方图得出中位数的内容，要掌握在频率分布直方图中，中位数使得直方图左右两侧频率相等，即使得直方图左右两侧面积相等．

知识点：1.算法与程序框图

D

【考点】循环结构．

【专题】图表型；算法和程序框图．

【分析】模拟执行程序框图，依次写出每次循环得到的x的值，当x=﹣3时不满足条件x≥0，计算并输出y的值为10．

【解答】解：模拟执行程序框图，可得

x=6

x=3

满足条件x≥0，x=0

满足条件x≥0，x=﹣3

不满足条件x≥0，y=10

输出y的值为10．

故选：D．

【点评】本题主要考查了循环结构的程序框图，正确写出每次循环得到的x的值是解题的关键，属于基础题．

知识点：2.古典概型

D

【考点】模拟方法估计概率．

【专题】计算题；概率与统计．

【分析】由题意知模拟射击4次的结果，经随机模拟产生了如下20组随机数，在20组随机数中表示种射击4次至少击中3次的有多少组，可以通过列举得到共多少组随机数，根据概率公式，得到结果．

【解答】解：由题意知模拟射击4次的结果，经随机模拟产生了如下20组随机数，

在20组随机数中表示射击4次至少击中3次的有：7527 0293 9857 0347 4373 8636 9647 4698 6233 2616 8045 3661 9597 7424 4281，共15组随机数，

∴所求概率为0.75．

故选：D．

【点评】本题考查模拟方法估计概率、随机数的含义与应用，是一个基础题，解这种题目的主要依据是等可能事件的概率，注意列举法在本题的应用．

知识点：4.回归分析的基本思想及其初步应用

D

【考点】线性回归方程．

【专题】计算题；概率与统计．

【分析】求出这组数据的横标和纵标的平均数，写出这组数据的样本中心点，把样本中心点代入线性回归方程求出m的值．

【解答】解：∵==， =，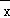

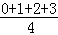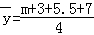∴这组数据的样本中心点是（，），

∵关于y与x的线性回归方程=2.1x+0.85，

∴=2.1×+0.85，解得m=0.5，

∴m的值为0.5．

故选：D．

【点评】本题考查回归分析，考查样本中心点满足回归直线的方程，考查求一组数据的平均数，是一个运算量比较小的题目，并且题目所用的原理不复杂，是一个好题．

知识点：3.单调性与最大（小）值

（3，+∞）

【考点】复合函数的单调性．

【专题】函数的性质及应用．

【分析】先求出函数的定义域，然后将复合函数分解为内、外函数，分别讨论内外函数的单调性，进而根据复合函数单调性“同增异减”的原则，得到函数y=log3（x2﹣2x﹣3）的单调递增区间

【解答】解：函数y=log3（x2﹣2x﹣3）的定义域为（﹣∞，﹣1）∪（3，+∞）

令t=x2﹣2x﹣3，则y=log3t

∵y=log3t为增函数

t=x2﹣2x﹣3在（﹣∞，﹣1）上为减函数；

在（3，+∞）为增函数

∴函数y=log3（x2﹣2x﹣3）的单调递增区间为（3，+∞）

故答案为：（3，+∞）

【点评】本题考查的知识点是复合函数的单调性，二次函数的性质，对数函数的单调性，其中复合函数单调性“同增异减”是解答本题的关键，本题易忽略真数大于为，而错答为（1，+∞）

知识点：3.几何概型

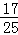
【考点】简单线性规划的应用；几何概型．

【专题】计算题；概率与统计．

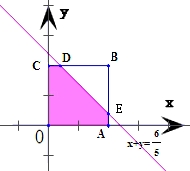
【分析】设取出的两个数分别为x、y，可得满足“x、y∈（0，1）”的区域为横纵坐标都在（0，1）之间的正方形内部，而事件“两数之和小于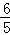”对应的区域为正方形的内部且在直线x+y=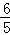下方的部分，根据题中数据分别计算两部分的面积，由几何概型的计算公式可得答案．

【解答】解：设取出的两个数分别为x、y，可得0＜x＜1且0＜y＜1，

满足条件的点（x，y）所在的区域为横纵坐标都在（0，1）之间的

正方形内部，即如图的正方形OABC的内部，其面积为S=1×1=1，

若两数之和小于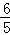，即x+y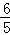＜，对应的区域为直线x+y=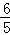下方，

且在正方形OABC内部，即如图的阴影部分．

∵直线x+y=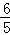分别交BC、AB于点D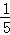（，1）、E（1，），

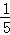∴S△BDE=××=．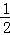

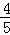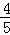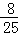因此，阴影部分面积为S'=SABCD﹣S△BDE=1﹣=．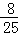

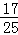由此可得：两数之和小于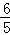的概率为P==．

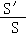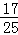故答案为：．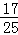

【点评】本题给出在区间（0，1）内随机地取出两个数，求两数之和小于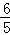的概率．着重考查了二元一次不等式组表示的平面区域、正方形和三角形的面积公式、几何概型计算公式等知识点，属于中档题．

知识点：1.算法与程序框图

k≤10（或k＜11）

【考点】程序框图．

【专题】算法和程序框图．

【分析】程序框图的功能是求S=1×12×11×…，由程序运行的结果为S=132，得终止程序时，k=10，从而求出判断框的条件．

【解答】解：由题意知，程序框图的功能是求S=1×12×11×…，

∵程序运行的结果为S=132，∴终止程序时，k=10，

∴判断框的条件是k≤10（或k＜11），

故答案是k≤10（或k＜11），

【点评】本题是当型循环结构的程序框图，解题的关键是判断程序框图功能及判断终止程序的k值．

知识点：12.绝对值函数与分段函数及其他函数

[﹣1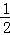，﹣）∪﹙0，1]

【考点】函数单调性的性质．

【专题】函数的性质及应用．

【分析】由已知中函数的解析式为分段函数，故可分当﹣1≤x＜0时和0＜x≤1时两种情况，结合函数的解析式，将不等式f（x）﹣f（﹣x）＞﹣1具体化，最后综合讨论结果，可得答案．

【解答】解：当﹣1≤x＜0时，则：0＜﹣x≤1

f（x）=﹣x﹣1，f（﹣x）=﹣（﹣x）+1=x+1

f（x）﹣f（﹣x）＞﹣1，

即：﹣2x﹣2＞﹣1，

得：x＜﹣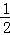

又因为：﹣1≤x＜0

所以：﹣1≤x＜﹣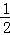

当0＜x≤1时，则：﹣1≤﹣x＜0

此时：f（x）=﹣x+1，f（﹣x）=﹣（﹣x）﹣1=x﹣1

f（x）﹣f（﹣x）＞﹣1，

即：﹣2x+2＞﹣1，

得：x＜3/2

又因为：0＜x≤1

所以：0＜x≤1

综上，原不等式的解集为：[﹣1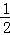，﹣）∪（0，1]

故答案为：[﹣1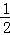，﹣）∪（0，1]

【点评】本题考查的知识点是分段函数，不等式的解法，其中利用分类讨论思想根据函数解析式将抽象不等式具体化是解答的关键．

知识点：5.奇偶性与周期性

0

【考点】函数奇偶性的性质；函数的周期性．

【专题】函数思想；转化法；函数的性质及应用．

【分析】根据条件判断函数的周期性，利用函数奇偶性和周期性的关系进行转化求解即可．

【解答】解：∵设f（x）是定义在R上的奇函数，且对任意实数x都有f（x+2）=﹣f（x），

∴f（x+4）=﹣f（x+2）=f（x），

∴函数f（x）是周期为4的周期函数，

∵当x∈[0，2]时，f（x）=2x﹣x2，

∴f（0）=0，f（1）=2﹣1=1，f（2）=0，f（3）=﹣1，

∴f（0）+f（1）+f（2）+…+f（2015）=504×[f（0）+f（1）+f（2）+f（3）]=504×（0+1+1﹣1）=0．

故答案为：0

【点评】本题主要考查函数值的计算，根据条件判断函数的周期性是解决本题的关键．

知识点：2.用样本估计总体

【考点】列举法计算基本事件数及事件发生的概率；分层抽样方法．

【专题】计算题；整体思想；定义法；概率与统计．

【分析】（1）用苹果的重量在[90，95）的频数除以样本容量，即为所求．

（2）根据重量在[80，85）的频数所占的比例，求得重量在[80，85）的苹果的个数．

（3）用列举法求出所有的基本事件的个数，再求出满足条件的事件的个数，即可得到所求事件的概率．

【解答】解：（1）重量在[90，95）的频率为；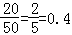

（2）由x+10+20+15=50得x=5，所以重量在[80，85）的个数为：；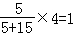

（3）由（2）知，重量在[80，85）的个数为1，记为x重量在[95，100）的个数为3，记为a，b，c．从抽取的4个苹果中任取2个，基本事件有：（x，a），（x，b），（x，c），（a，b），（a，c），（b，c）6种，其中满足“重量之差的绝对值大于5”即：抽取的两个苹果重量在[80，85）和[95，100）中各一个，包含（x，a），（x，b），（x，c）3种情况，所以概率为：．

【点评】本题考查古典概型问题，用列举法计算可以列举出基本事件和满足条件的事件，应用列举法来解题是这一部分的最主要思想．本题还考查分层抽样的定义和方法，利用了总体中各层的个体数之比等于样本中对应各层的样本数之比，属于基础题．

知识点：4.回归分析的基本思想及其初步应用

【考点】线性回归方程．

【专题】函数思想；综合法；概率与统计．

【分析】（I）根据回归系数公式计算回归系数，得到回归方程，并用回归方程进行数值估计；

（II）（1）求出5组即时均值，根据方差公式计算方差；

（2）利用古典概型的概率公式计算．

【解答】解：（Ⅰ）经计算可得：，，，，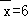

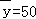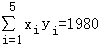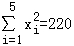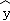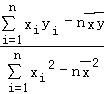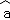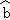所以： ==12， =﹣=﹣22，

从而得回归直线方程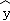=12x﹣22．

当x=10时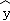， =12x﹣22=12×12﹣22=122．

该演员上春晚12次时的粉丝数量122万人．

（Ⅱ）经计算可知，这五组数据对应的“即时均值”分别为：5，5，7，10，10，

（1）这五组“即时均值”的平均数为：7.4，则方差为；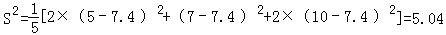

（2）这五组“即时均值”可以记为A1，A2，B，C1，C2，从“即时均值”中任选3组，选法共有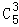=10种情况，

其中不超过20的情况有（A1，A2，B），（A1，C1，C2），（A2，C1，C2）共3种情况，故所求概率为：．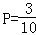

【点评】本题考查了利用最小二乘法求回归直线方程，结合回归直线方程进行预测，平均数、方差的计算，古典概型的计算．属于基础题．

知识点：1.算法与程序框图

【考点】程序框图；古典概型及其概率计算公式；几何概型．

【专题】综合题；概率与统计．

【分析】（1）根据分层抽样可得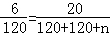，故可求n的值；

（2）求出高二代表队6人，从中抽取2人上台抽奖的基本事件，确定a和b至少有一人上台抽奖的基本事件，根据古典概型的概率公式，可得a和b至少有一人上台抽奖的概率；

（3）确定满足0≤x≤1，0≤y≤1点的区域，由条件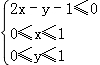得到的区域为图中的阴影部分，计算面积，可求该代表中奖的概率．

【解答】解：（1）由题意可得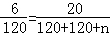，∴n=160；

（2）高二代表队6人，从中抽取2人上台抽奖的基本事件有（a，b），（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b．f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共15种，其中a和b至少有一人上台抽奖的基本事件有9种，

∴a和b至少有一人上台抽奖的概率为=；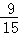

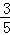（3）由已知0≤x≤1，0≤y≤1，点（x，y）在如图所示的正方形OABC内，

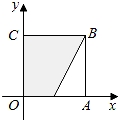
由条件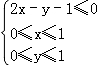得到的区域为图中的阴影部分

由2x﹣y﹣1=0，令y=0可得x=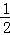，令y=1可得x=1

∴在x，y∈[0，1]时满足2x﹣y﹣1≤0的区域的面积为=

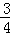
∴该代表中奖的概率为=．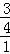

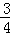【点评】本题考查概率与统计知识，考查分层抽样，考查概率的计算，确定概率的类型是关键．

知识点：6.二次函数

【考点】函数恒成立问题；函数的零点与方程根的关系．

【专题】函数的性质及应用．

【分析】（1）由函数g（x）=a（x﹣1）2+1+b﹣a，a＞0，所以g（x）在区间[2，3]上是增函数，故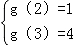，由此解得a、b的值．

（2）不等式可化为 2x+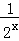﹣2≥k•2x，故有 k≤t2﹣2t+1，t∈[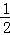，2]，求出h（t）=t2﹣2t+1的最小值，从而求得k的取值范围．

（3）方程f（|2k﹣1|）+k•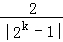﹣3k=0⇒|2x﹣1|2﹣（2+3k）|2x﹣1|+（1+2k）=0，（|2x﹣1|≠0），令|2x﹣1|=t，则t2﹣（2+3k）t+（1+2k）=0（t≠0），构造函数h（t）=t2﹣（2+3k）t+（1+2k），通过数形结合与等价转化的思想即可求得k的范围．

【解答】解：（1）函数g（x）=ax2﹣2ax+b+1=a（x﹣1）2+1+b﹣a，

因为a＞0，所以g（x）在区间[2，3]上是增函数，

故，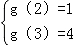

即，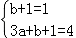

解得．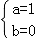

（2）由已知可得f（x）=x+﹣2，

所以，不等式f（2x）﹣k•2x≥0可化为 2x+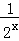﹣2≥k•2x，

可化为 1+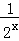（）2﹣2•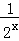≥k，令t=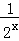，则 k≤t2﹣2t+1．

因 x∈[﹣1，1]，故 t∈[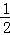，2]．故k≤t2﹣2t+1在t∈[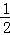，2]上恒成立．

记h（t）=t2﹣2t+1，因为 t∈[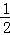，2]，故 h（t）min=h（1）=0，

所以k的取值范围是（﹣∞，0]．

（3）方程f（|2k﹣1|）+k•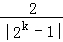﹣3k=0可化为：

|2x﹣1|2﹣（2+3k）|2x﹣1|+（1+2k）=0，|2x﹣1|≠0，

令|2x﹣1|=t，则方程化为

t2﹣（2+3k）t+（1+2k）=0（t≠0），

∵方程f（|2k﹣1|）+k•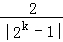﹣3k=0有三个不同的实数解，

∴由t=|2x﹣1|的图象知，

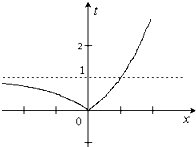
t2﹣（2+3k）t+（1+2k）=0（t≠0），有两个根t1、t2，

且0＜t1＜1＜t2或0＜t1＜1，t2=1．

记h（t）=t2﹣（2+3k）t+（1+2k），

则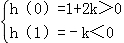，或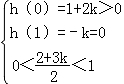

∴k＞0．

【点评】本题考查二次函数在闭区间上的最值，考查函数恒成立问题问题，考查数形结合与等价转化、函数与方程思想的综合应用，属于难题．