(5分)已知集合 ,则M∩N=( )
,则M∩N=( )
A.
[0,+∞)
B.
[﹣2,2]
C.
[0,2]
D.

知识点:3.集合的基本运算
C
集合M={x|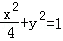 }=[﹣2,2]
}=[﹣2,2]
集合N={y|y=lg(x2+1)}=[0,+∞)
∴M∩N=[0,2]
故选:C.
(5分)已知复数z1=1﹣i,z2=2+i,则复数 对应的点位于复平面内的( )
对应的点位于复平面内的( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
知识点:3.复数代数形式的四则运算
D
∵z1=1﹣i,z2=2+i,
∴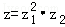 =(1﹣i)2(2+i)=(1﹣2i+i2)(2+i)=2﹣4i,
=(1﹣i)2(2+i)=(1﹣2i+i2)(2+i)=2﹣4i,
因为点(2,﹣4)位于第四象限,
故对应的点位于复平面内的第四象限,
故选D
(5分)下列说法中,不正确的是( )
A.
命题p: x∈R,sinx≤1,则¬p:
x∈R,sinx≤1,则¬p: x∈R,sinx>1
x∈R,sinx>1
B.
在△ABC中,“A>30°”是“sinA> ”的必要不充分条件
”的必要不充分条件
C.
命题p:点 为函数
为函数 的一个对称中心.命题q:如果
的一个对称中心.命题q:如果 ,那么
,那么 在
在 方向上的投影为1.则(¬p)∨(¬q)为真命题
方向上的投影为1.则(¬p)∨(¬q)为真命题
D.
命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题.
知识点:5.充分条件与必要条件
D
命题p: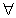 x∈R,sinx≤1的否定是:
x∈R,sinx≤1的否定是: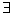 x∈R,sinx>1,故A正确;
x∈R,sinx>1,故A正确;
在△ABC中,若A>150°此时sinA<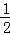 ,故“A>30°”是“sinA>
,故“A>30°”是“sinA>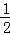 ”的不充分条件,
”的不充分条件,
但“sinA>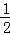 ”时,30°<A<150°,故“A>30°”是“sinA>
”时,30°<A<150°,故“A>30°”是“sinA>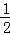 ”的必要条件,
”的必要条件,
故B正确;
函数 的对称中心坐标为(
的对称中心坐标为( +
+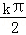 ,0),k
,0),k Z,令
Z,令 +
+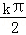 =
=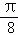 ,则k=
,则k=
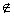 Z,故命题p为假命题;
Z,故命题p为假命题;
∵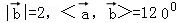 ,则那么
,则那么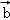 在
在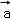 方向上的投影为2•cos120°=﹣1,故命题q为假命题;
方向上的投影为2•cos120°=﹣1,故命题q为假命题;
则(¬p)∨(¬q)为真命题,故C正确;
命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为“在△ABC中,若sinA≠sinB,则△ABC为不等腰三角形”,当A=C=45°时,sinA≠sinB,但三角形为等腰三角形,故为假命题,故D错误
故选D
(5分)已知两条不重合的直线m、n和两个不重合的平面α、β,有下列命题:
①若m⊥n,m⊥α,则n∥α;
②若m⊥α,n⊥β,m∥n,则α∥β;
③若m、n是两条异面直线,m α,n
α,n β,m∥β,n∥α,则α∥β;
β,m∥β,n∥α,则α∥β;
④若α⊥β,α∩β=m,n β,n⊥m,则n⊥α.
β,n⊥m,则n⊥α.
其中正确命题的个数是( )
A.
1
B.
2
C.
3
D.
4
知识点:5.直线、平面平行的判定及其性质
C
①若m⊥n,m⊥α,则n可能在平面α内,故①错误
②∵m⊥α,m∥n,∴n⊥α,又∵n⊥β,∴α∥β,故②正确
③过直线m作平面γ交平面β与直线c,
∵m、n是两条异面直线,∴设n∩c=O,
∵m∥β,m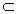 γ,γ∩β=c∴m∥c,
γ,γ∩β=c∴m∥c,
∵m α,c
α,c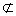 α,∴c∥α,
α,∴c∥α,
∵n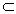 β,c
β,c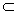 β,n∩c=O,c∥α,n∥α
β,n∩c=O,c∥α,n∥α
∴α∥β;故③正确
④由面面垂直的性质定理:∵α⊥β,α∩β=m,n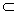 β,n⊥m,∴n⊥α.故④正确
β,n⊥m,∴n⊥α.故④正确
故正确命题有三个,
故选C
(5分)(2010•茂名二模)如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC′上的高,则 •
• 的值等于( )
的值等于( )

A.
0
B.
4
C.
8
D.
﹣4
知识点:4.平面向量的数量积(夹角、模)
B
因为AB=BC=4,∠ABC=30°,AD是边BC上的高,
所以AD=4sin30°=2.
所以 •
• =
= •(
•( +
+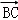 )=
)= •
• +
+ •
•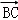 =
=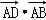 =2×4×
=2×4×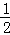 =4,
=4,
故选B
(5分)若不等式a>|t﹣1|﹣|t﹣2|对任意t∈R恒成立,则函数 的单调递减区间为( )
的单调递减区间为( )
A.

B.
(3,+∞)
C.

D.
(﹣∞,2)
知识点:3.单调性与最大(小)值
B
设y=|t﹣1|﹣|t﹣2|,由t﹣1=0,得t=1;由t﹣2=0,得t=2.
当t≥2时,y=t﹣1﹣t+2=1;
当1≤t<2时,y=t﹣1﹣2+t=2t﹣3∈[﹣1,1);
当t<1时,y=1﹣t﹣2+t=﹣1.
∴y=|t﹣1|﹣|t﹣2|的值域是[﹣1,1].
∵不等式a>|t﹣1|﹣|t﹣2|对任意t∈R恒成立,∴a>1.∴0< <1.
<1.
∵函数 ,
,
∴x2﹣5x+6>0,解得x>3,或x<2.
∵m=x2﹣5x+6是开口向上,对称轴为x= 的抛物线,
的抛物线,
∴函数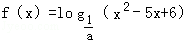 的单调递减区间为(3,+∞).
的单调递减区间为(3,+∞).
故选B.
(5分)设f′(x)为函数f(x)的导函数,且 ,则
,则 与
与 的大小关系是( )
的大小关系是( )
A.

B.

C.

D.
不能确定
知识点:2.任意角的三角函数
C
∵f′(x)为函数f(x)的导函数,且 ,
,
∴f′(x)=cosx+2f′( ),
),
∴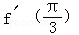 =cos
=cos +2
+2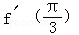 ,解得
,解得 =﹣
=﹣ .
.
∴f′(x)=cosx﹣1.
由f′(x)=cosx﹣1=0,得x=0+2kπ,k∈Z.
∵当x∈(0,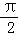 )时,f′(x)<0,
)时,f′(x)<0,
∴当x∈(0,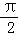 )时,f(x)是减函数,
)时,f(x)是减函数,
∴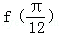 >
>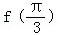 .
.
故选C.
(5分)设x,y满足约束条件 ,若目标函数
,若目标函数 的最大值为2,则a+b的最小值为( )
的最大值为2,则a+b的最小值为( )
A.

B.

C.

D.
4
知识点:3.二元一次不等式(组)与简单的线性规划
D
满足约束条件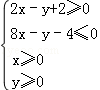 的区域是一个四边形,
的区域是一个四边形,
如图,4个顶点是(0,0),(0,2),( ,0),(1,4),
,0),(1,4),
由图易得目标函数在(1,4)取最大值2,即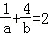 ,
,
∴a+b= (a+b)(
(a+b)( )=
)= (5+
(5+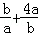 )
)
∵a>0,b>0,∴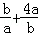 ≥
≥ =4
=4
当且仅当 时,
时,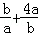 的最小值问4
的最小值问4
∴a+b的最小值为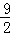
故选A.
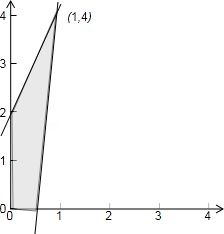
(5分)如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=( )

A.

B.

C.

D.

知识点:2.空间几何体的三视图和直观图
D
三视图复原的几何体如图,
它是底面为等腰直角三角形,一条侧棱垂直底面的一个顶点,
它的外接球,就是扩展为长方体的外接球,
外接球的直径是2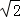 ,
,
该几何体的外接球的体积V1=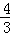 π(
π(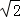 )3=
)3= π.
π.
V2=2×( π)=
π)=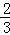 π,
π,
∴V1:V2=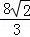 π:
π: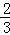 π=4
π=4 .
.
故选D.

(5分)若数列{an}满足 (p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合
(p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合 ,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为( )
,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为( )
A.
64
B.
63
C.
32
D.
31
知识点:4.等比数列及其性质
B
设数列{an}为正数等方差数列,p为公方差,则
 ,
,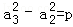 ,
, ,
,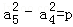
∴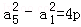
∵a1=1,∴a2=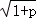 ,a5=
,a5=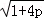
∵a1,a2,a5成等比数列,
∴1+p=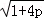
∴p=0或p=2
∵a1≠a2,∴p=2
∴an= =
=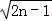
∴ =
=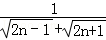 =
=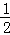 (
( ﹣
﹣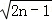 )
)
∴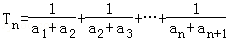 =
=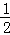 (
(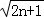 ﹣1)
﹣1)
∴A中的整数元素为1,2,3,4,5,6
∵A的非空子集B,若B的元素都是整数,
∴集合A中的完美子集的个数为26﹣1=63
故选B.
(5分)(2010·上饶模拟) a∈(﹣∞,0),总
a∈(﹣∞,0),总 x0使得acosx+a≥0成立,则
x0使得acosx+a≥0成立,则 的值为 .
的值为 .
知识点:4.和角公式与倍(半)角公式
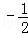
∵a∈(﹣∞,0),acosx0+a≥0
∴cosx0≤﹣1
∴x0=2kπ+π
∴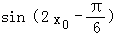 =sin(4kπ+2π﹣
=sin(4kπ+2π﹣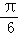 )=﹣sin
)=﹣sin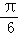 =﹣
=﹣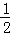
故答案为﹣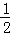
(5分)(2011•陕西)设f(x)= 若f(f(1))=1,则a= .
若f(f(1))=1,则a= .
知识点:6.微积分的基本定理
1
∵f(x)=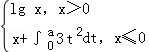
∴f(1)=0,则f(f(1))=f(0)=1
即∫0a3t2dt=1=t3|0a=a3
解得:a=1
故答案为:1
(5分)已知f(x)是定义在R上连续的偶函数,f(x)的图象向右平移一个单位长度又得到一个奇函数,且f(2)=﹣1.则f(8)+f(9)+f(10)+…+f(2012)= .
知识点:5.奇偶性与周期性
1
∵f(x)是R上的偶函数,
∴f(x)=f(﹣x) 用x+1换x,即f(x+1)=f(﹣x﹣1)①
∵将f(x)的图象向右平移一个单位后,得到一个奇函数的图象,
∴函数f(x)的图象的对称中心(﹣1,0),有f(﹣1)=0,且f(﹣1﹣x)=﹣f(﹣1+x) ②
∴由①②得f(x+1)=﹣f(﹣1+x),可得f(x+2)=﹣f(x),得到f(x+4)=f(x),
∴函数f(x)存在周期T=4,
∵f(2)=﹣1,f(﹣1)=0,
利用条件可以推得:f(﹣1)=f(1)=0,f(2)=﹣1=﹣f(0),f(3)=f(4﹣1)=0,
f(﹣3)=f(3)=0,f(4)=f(0)=1,
所以在一个周期中f(1)+f(2)+f(3)+f(4)=0,
∴f(8)+f(9)+f(10)+…+f(2012)=f(8)=f(4)=1.
故答案为:1.
(5分)(2013•杨浦区一模)在平面直角坐标系xOy中,设直线 和圆x2+y2=n2相切,其中m,n∈N,0<|m﹣n|≤1,若函数f(x)=mx+1﹣n的零点x0∈(k,k+1)k∈Z,则k= .
和圆x2+y2=n2相切,其中m,n∈N,0<|m﹣n|≤1,若函数f(x)=mx+1﹣n的零点x0∈(k,k+1)k∈Z,则k= .
知识点:4.直线与圆的位置关系
0.
∵直线 和圆x2+y2=n2相切,
和圆x2+y2=n2相切,
∴圆心到直线的距离是半径n,
∴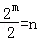
∴2m=2n,
∵m,n∈N,0<|m﹣n|≤1,
∴m=3,n=4,
∴函数f(x)=mx+1﹣n=3x+1﹣4,
要求函数的零点所在的区间,
令f(x)=0,
即3x+1﹣4=0,
∴3x+1=4,
∴x+1=log34,
∴x=log34﹣1
∵log34∈(1,2)
∴x∈(0,1)
∴k=0
故答案为:0
(12分)在△ABC中,角A,B,C的对边为a,b,c,点(a,b)在直线x(sinA﹣sinB)+ysinB=csinC上.
(I)求角C的值;
(II)若a2+b2=6(a+b)﹣18,求△ABC的面积.
知识点:9.正弦定理和余弦定理(解三角形)
(1) 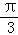 (2)
(2) 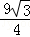
(I)由题得a(sinA﹣sinB)+bsinB=csinC,
由正弦定理得a(a﹣b)+b2=c2,即a2+b2﹣c2=ab.
∴余弦定理得cosC=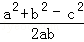 =
= ,
,
∵C∈(0,π),
∴C=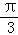 .…(6分)
.…(6分)
(II)∵a2+b2=6(a+b)﹣18,∴(a﹣3)2+(b﹣3)2=0,从而a=b=3.
∵C=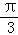 ,
,
∴△ABC是边长为3的等边三角形,可得△ABC的面积S= ×32=
×32=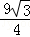 …(12分)
…(12分)
(12分)一盒中装有分别标记着1,2,3,4的4个小球,每次从袋中取出一只球,设每只小球被取出的可能性相同.
(1)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;
(2)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为ξ,求ξ的分布列与数学期望.
知识点:9.离散型随机变量的分布列、均值与方差
(1)当恰好第三次取出的球的标号为最大数字时,则第三次取出的球可能是3或4
得P=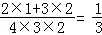
(2)ξ的可能取值为1,2,3,4
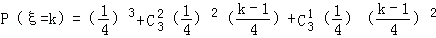 ,
,
ξ的分布列为:
ξ | 1 | 2 | 3 | 4 |
P |
|
|
|
|
故  .
.
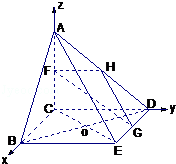
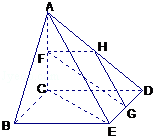
(12分)如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).
(1)求证:平面FHG∥平面ABE;
(2)记BC=x,V(x)表示三棱锥B﹣ACE的体积,求V(x)的最大值;
(3)当V(x)取得最大值时,求二面角D﹣AB﹣C的余弦值.Pn(xn,yn)

知识点:3.空间几何体的表面积与体积
(1)证明:由图(甲)结合已知条件知四边形CBED为正方形
如图(乙)∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)
∵CD∥BE∴FH∥BE
∵BE⊂面ABE,FH⊄面ABE
∴FH∥面ABE﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)
同理可得HG∥面ABE
又∵FH∩HG=H
∴平面FHG∥平面ABE﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)
(2)∵平面ACD⊥平面CBED 且AC⊥CD
∴AC⊥平面CBED﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)
∴V(x)=VA﹣BCE=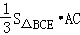
∵BC=x∴AC=2﹣x(0<x<2)
∴V(x)= =
=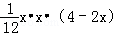 ﹣﹣﹣﹣(7分)
﹣﹣﹣﹣(7分)
∵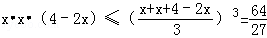
∴V(x)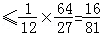
当且仅当x=4﹣2x即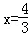 时取“=”
时取“=”
∴V(x)的最大值为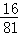 ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)
(3)以点C为坐标原点,CB为x轴建立空间直角坐标系
如右图示:由(2)知当V(x)取得最大值时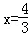 ,即BC=
,即BC=
这时AC=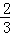 ,∴B
,∴B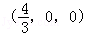 ,
,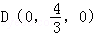 ,
,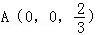 ﹣﹣﹣(10分)
﹣﹣﹣(10分)
∴平面ACB的法向量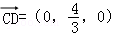
设平面ABD的法向量为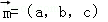
∵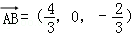 ,
,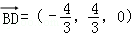 ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)
由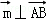 ,
,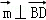 得
得 ,
,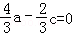
令c=1得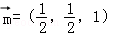 ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)
设二面角D﹣AB﹣C为θ,则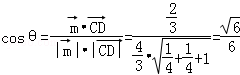 ﹣﹣﹣(14分)
﹣﹣﹣(14分)
(12分)等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)若不等式
 对n∈N*成立,求最小正整数m的值.
对n∈N*成立,求最小正整数m的值.
知识点:2.等差数列及其性质
(1)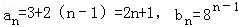 (2)2012.
(2)2012.
(1)设{an}的公差为d,{bn}的公比为q,则d为正整数,an=3+(n﹣1)d,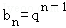
依题意,b2S2=64,b3S3=960,∴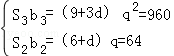
解得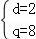 ,或
,或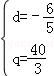 (舍去)
(舍去)
故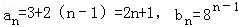
(2)Sn=3+5+…+(2n+1)=n(n+2)
∴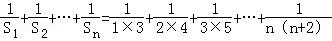 =
=
=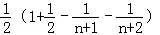 =
=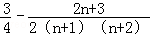

∴m≥2012,所以所求m的最小正整数是2012.
(13分)(2011•万州区一模)已知动圆C过点A(﹣2,0),且与圆M:(x﹣2)2+y2=64相内切
(1)求动圆C的圆心的轨迹方程;
(2)设直线l:y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线 交于不同两点E,F,问是否存在直线l,使得向量
交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
知识点:3.圆的方程
(1) (2)9.
(2)9.
(1)圆M:(x﹣2)2+x2=64,圆心M的坐标为(2,0),半径R=8.
∵|AM|=4<R,∴点A(﹣2,0)在圆M内,
设动圆C的半径为r,圆心为C,依题意得r=|CA|,且|CM|=R﹣r,
即
∴圆心C的轨迹是中心在原点,以A,M两点为焦点,长轴长为8的椭圆,
设其方程为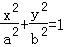 (a>b>0),则a=4,c=2,
(a>b>0),则a=4,c=2,
∴b2=a2﹣c2=12,∴所求动圆C的圆心的轨迹方程为 .
.
(2)由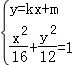 消去y 化简整理得:(3+4k2)x2+8kmx+4m2﹣48=0,
消去y 化简整理得:(3+4k2)x2+8kmx+4m2﹣48=0,
设B(x1,y1),D(x2,y2),则x1+x2=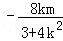 .
.
△1=(8km)2﹣4(3+4k2) (4m2﹣48)>0.①
由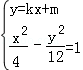 消去y 化简整理得:(3﹣k2)x2﹣2kmx﹣m2﹣12=0,
消去y 化简整理得:(3﹣k2)x2﹣2kmx﹣m2﹣12=0,
设E(x3,y3),F(x4,y4),则x3+x4=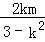 .
.
△2=(﹣2km)2+4(3﹣4k2) (m2+12)>0.②
∵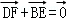 ,∴(x4﹣x2 )+(x3﹣x1)=0,即x1+x2=x3+x4,
,∴(x4﹣x2 )+(x3﹣x1)=0,即x1+x2=x3+x4,
∴ ,∴2km=0或
,∴2km=0或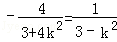 ,
,
解得k=0或m=0,
当k=0时,由①、②得 ,
,
∵m∈Z,∴m的值为﹣3,﹣2,﹣1,0,1,2,3;
当m=0时,由①、②得 ,
,
∵k∈Z,∴k=﹣1,0,1.
∴满足条件的直线共有9条.
(14分)设函数f(x)=x2,g(x)=alnx+bx(a>0)
(1)若f(1)=g(1),f′(1)=g′(1),求g(x)的解析式;
(2)在(1)的结论下,是否存在实常数k和m,使得f(x)≥kx+m和g(x)≤kx+m?若存在,求出k和m的值.若不存在,说明理由.
(3)设G(x)=f(x)+2﹣g(x)有两个零点x1和x2,且x1,x0x2成等差数列,试探究值G′(x0)的符号.
知识点:3.导数在研究函数中的应用
(1)g(x)=lnx+x;(2)存在这样的k和m,且k=2,m=﹣1,满足条件.(3)为正.
(1)由f(1)=g(1),得 b=1.
∵f′(x)=2x,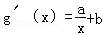 ,f′(1)=g′(1)
,f′(1)=g′(1)
∴2=a+b,联立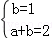 ,解得a=b=1,
,解得a=b=1,
则g(x)=lnx+x.
(2)因f(x)与g(x)有一个公共点(1,1),而函数f(x)=x2在点(1,1)的切线方程为y=2x﹣1,
下面验证 f(x)≥2x﹣1,g(x)≤2x﹣1 都成立即可.
由x2﹣2x+1≥0,得x2≥2x﹣1,知f(x)≥2x﹣1恒成立.
设h(x)=lnx+x﹣(2x﹣1),即h(x)=lnx﹣x+1, ,∴当0<x<1时,h′(x)>0;当x>1时,h′(x)<0.
,∴当0<x<1时,h′(x)>0;当x>1时,h′(x)<0.
∴h(x)在(0,1)上递增,在(1,+∞)上递减,∴h(x)在x=1时取得最大值,
∴h(x)=lnx+x﹣(2x﹣1)的最大值为h(1)=0,所以lnx+x≤2x﹣1恒成立.
故存在这样的k和m,且k=2,m=﹣1,满足条件.
(3)G′(x0)的符号为正,理由为:
∵G(x)=x2+2﹣alnx﹣bx有两个不同的零点x1,x2,
则有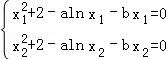 ,两式相减得x22﹣x12﹣a(lnx2﹣lnx1)﹣b(x2﹣x1)=0.
,两式相减得x22﹣x12﹣a(lnx2﹣lnx1)﹣b(x2﹣x1)=0.
即x1+x2﹣b=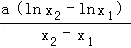 ,又x1+x2=2x0,
,又x1+x2=2x0,
则G′(x0)=2x0﹣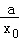 ﹣b=(x1+x2﹣b)﹣
﹣b=(x1+x2﹣b)﹣ =
=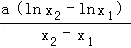 ﹣
﹣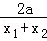 =
=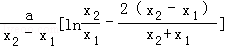
=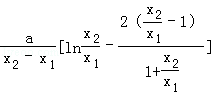 ,
,
①当0<x1<x2时,令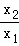 =t,则t>1,且G′(x0)=
=t,则t>1,且G′(x0)=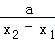 [lnt﹣
[lnt﹣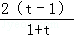 ],
],
故μ(t)=lnt﹣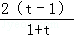 (t>1),μ′(t)=
(t>1),μ′(t)=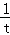 ﹣
﹣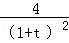 =
=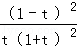 >0,则μ(t)在[1,+∞)上为增函数,
>0,则μ(t)在[1,+∞)上为增函数,
而μ(1)=0,∴μ(t)>0,即lnt﹣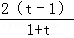 >0,又a>0,x2﹣x1>0,∴G′(x0)>0,
>0,又a>0,x2﹣x1>0,∴G′(x0)>0,
②当0<x2<x1时,同理可得:G′(x0)>0,
综上所述:G′(x0)值的符号为正.