从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
A.至少有一个红球与都是红球
B.至少有一个红球与都是白球
C.至少有一个红球与至少有一个白球
D.恰有一个红球与恰有二个红球
知识点:4.互斥事件及其发生的概率
D
【考点】互斥事件与对立事件.
【分析】分析出从装有5个红球和3个白球的口袋内任取3个球的所有不同的情况,然后利用互斥事件和对立事件的概念逐一核对四个选项即可得到答案.
【解答】解:从装有5个红球和3个白球的口袋内任取3个球,不同的取球情况共有以下几种:
3个球全是红球;2个红球1个白球;1个红球2个白球;3个球全是白球.
选项A中,事件“都是红球”是事件“至少有一个红球”的子事件;
选项B中,事件“至少有一个红球”与事件“都是白球”是对立事件;
选项C中,事件“至少有一个红球”与事件“至少有一个白球”的交事件为“2个红球1个白球”与“1个红球2个白球”;
选项D中,事件“恰有一个红球”与事件“恰有二个红球”互斥不对立.
故选:D.
已知 =1﹣bi,其中a,b是实数,i是虚数单位,则|a﹣bi|=( )
=1﹣bi,其中a,b是实数,i是虚数单位,则|a﹣bi|=( )
A.3 B.2 C.5 D.
知识点:3.复数代数形式的四则运算
D
【考点】复数求模.
【分析】通过复数的相等求出a、b,然后求解复数的模.
【解答】解: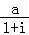 =1﹣bi,
=1﹣bi,
可得a=1+b+(1﹣b)i,因为a,b是实数,
所以 ,解得a=2,b=1.
,解得a=2,b=1.
所以|a﹣bi|=|2﹣i|=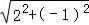 =
=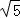 .
.
故选:D.
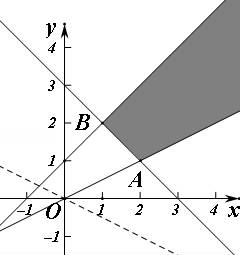
已知实数x,y满足不等式组 ,则z=x+2y的最小值为( )
,则z=x+2y的最小值为( )
A.﹣4 B.5 C.4 D.无最小值
知识点:3.二元一次不等式(组)与简单的线性规划
C
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用z的几何意义,即可求出z的最大值.
【解答】解:作出不等式组对应的平面区域如图:
设z=x+2y,则y=﹣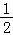 x+
x+
平移此直线,由图象可知当直线y=﹣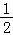 x+
x+ 经过A时,直线在y轴的截距最小,得到z最小,由
经过A时,直线在y轴的截距最小,得到z最小,由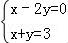 得到A(2,1),
得到A(2,1),
所以z=x+2y的最小值为2+2×1=4;
故选C.
“sinα=cosα”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
B
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分必要条件的定义结合集合的包含关系判断即可.
【解答】解:由“sinα=cosα”得:α=kπ+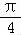 ,k∈Z,
,k∈Z,
故sinα=cosα是“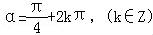 ”的必要不充分条件,
”的必要不充分条件,
故选:B.
一个体积为12 的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为( )
的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为( )

A.6 B.8 C.8
B.8 C.8 D.12
D.12
知识点:2.空间几何体的三视图和直观图
A
【考点】由三视图求面积、体积.
【分析】此几何体是一个正三棱柱,正视图即内侧面,底面正三角形的高是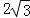 ,由正三角形的性质可以求出其边长,由于本题中体积已知,故可设出棱柱的高,利用体积公式建立起关于高的方程求高,再由正方形的面积公式求侧视图的面积即可.
,由正三角形的性质可以求出其边长,由于本题中体积已知,故可设出棱柱的高,利用体积公式建立起关于高的方程求高,再由正方形的面积公式求侧视图的面积即可.
【解答】解:设棱柱的高为h,
由左视图知,底面正三角形的高是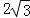 ,由正三角形的性质知,其边长是4,
,由正三角形的性质知,其边长是4,
故底面三角形的面积是 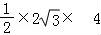 =4
=4 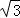
由于其体积为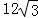 ,故有h×
,故有h×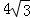 =
=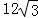 ,得h=3
,得h=3
由三视图的定义知,侧视图的宽即此三棱柱的高,故侧视图的宽是3,其面积为3×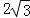 =
=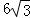
故选A
设向量 ,
, 满足|
满足| |=2,
|=2, 在
在 方向上的投影为1,若存在实数λ,使得
方向上的投影为1,若存在实数λ,使得 与
与 ﹣λ
﹣λ 垂直,则λ=( )
垂直,则λ=( )
A. B.1 C.2 D.3
B.1 C.2 D.3
知识点:4.平面向量的数量积(夹角、模)
C
【考点】平面向量数量积的运算.
【分析】利用向量投影的意义可得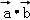 ,再利用向量垂直与数量积的关系即可得出.
,再利用向量垂直与数量积的关系即可得出.
【解答】解:∵向量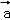 ,
,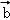 满足|
满足|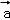 |=2,
|=2,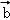 在
在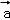 方向上的投影为1,
方向上的投影为1,
∴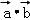 =
=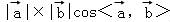 =2×1=2.
=2×1=2.
∵存在实数λ,使得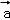 与
与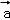 ﹣λ
﹣λ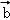 垂直,
垂直,
∴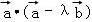 =
=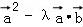 =0,
=0,
∴22﹣2λ=0,
解得λ=2.
故选:C.
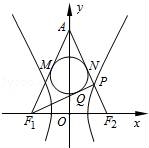
如图,已知双曲线 ﹣
﹣ =1(a>0,b>0)的左右焦点分别为F1,F2,|F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1,F2,|F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )

A.3 B.2 C. D.
D.
知识点:2.双曲线
B
【考点】双曲线的简单性质.
【分析】由|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,根据切线长定理,可得|PF1|﹣|PF2|=2,结合|F1F2|=4,即可得出结论.
【解答】解:由题意,∵|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,
∴根据切线长定理可得AM=AN,F1M=F1Q,PN=PQ,
∵|AF1|=|AF2|,
∴AM+F1M=AN+PN+NF2,
∴F1M=PN+NF2=PQ+PF2
∴|PF1|﹣|PF2|=F1Q+PQ﹣PF2=F1M+PQ﹣PF2=PQ+PF2+PQ﹣PF2=2PQ=2,
∵|F1F2|=4,
∴双曲线的离心率是e=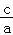 =2.
=2.
故选:B.
已知f(x)是定义在R上的减函数,其导函数f′(x)满足 +x<1,则下列结论正确的是( )
+x<1,则下列结论正确的是( )
A.对于任意x∈R,f(x)<0 B.对于任意x∈R,f(x)>0
C.当且仅当x∈(﹣∞,1),f(x)<0 D.当且仅当x∈(1,+∞),f(x)>0
知识点:3.导数在研究函数中的应用
B
【考点】利用导数研究函数的单调性.
【分析】由题意可得[(x﹣1)f(x)]′>0,结合函数的单调性,从而可判断当x>1时,f(x)>0,结合f(x)为减函数可得结论.
【解答】解:∵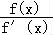 +x<1,f(x)是定义在R上的减函数,f′(x)<0,
+x<1,f(x)是定义在R上的减函数,f′(x)<0,
∴f(x)+f′(x)x>f′(x),
∴f(x)+f′(x)(x﹣1)>0,
∴[(x﹣1)f(x)]′>0,
∴函数y=(x﹣1)f(x)在R上单调递增,
而x=1时,y=0,则x<1时,y<0,
当x∈(1,+∞)时,x﹣1>0,故f(x)>0,
又f(x)是定义在R上的减函数,
∴x≤1时,f(x)>0也成立,
∴f(x)>0对任意x∈R成立,
故选:B.
已知集合A={x|3≤x<7},B={x|4<x<10},则A∪B= ,(∁RA)∩B= .
知识点:3.集合的基本运算
{x|3≤x<10},{x|7≤x<10}.
【考点】交、并、补集的混合运算.
【分析】根据并集、补集和交集的定义,分别写出对应的运算结果即可.
【解答】解:集合A={x|3≤x<7},B={x|4<x<10},
所以A∪B={x|3≤x<10},
∁RA={x|x<3或x≥7},
所以(∁RA)∩B={x|7≤x<10}.
故答案为:{x|3≤x<10},{x|7≤x<10}.
已知函数f(x)= sin xcos x+cos2x+a;则f(x)的最小正周期为 ,若f(x)在区间[﹣
sin xcos x+cos2x+a;则f(x)的最小正周期为 ,若f(x)在区间[﹣ ,
, ]上的最大值与最小值的和为
]上的最大值与最小值的和为 ,则实数a的值为 .
,则实数a的值为 .
知识点:4.和角公式与倍(半)角公式
π;0.
【考点】三角函数中的恒等变换应用.
【分析】利用两角和与差的正弦函数可求得f(x)=sin(2x+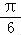 )+
)+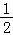 +a,从而可求f(x)的最小正周期;由﹣
+a,从而可求f(x)的最小正周期;由﹣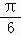 ≤x≤
≤x≤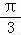 ⇒﹣
⇒﹣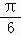 ≤2x+
≤2x+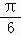 ≤
≤ ⇒﹣
⇒﹣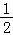 ≤sin(2x+
≤sin(2x+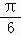 )≤1,从而可求f(x)在区间[﹣
)≤1,从而可求f(x)在区间[﹣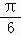 ,
,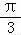 ]上的值域为[a,a+
]上的值域为[a,a+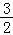 ],继而依题意可求a的值.
],继而依题意可求a的值.
【解答】解:∵f(x)=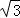 sin xcos x+cos2x+a=sin(2x+
sin xcos x+cos2x+a=sin(2x+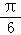 )+
)+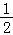 +a,
+a,
∴其最小正周期T=π;
∵x∈[﹣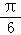 ,
,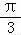 ]
]
∴2x+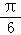 ∈[﹣
∈[﹣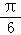 ,
, ],
],
∴﹣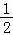 ≤sin(2x+
≤sin(2x+ )≤1,
)≤1,
∴a≤sin(2x+ )+
)+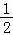 +a≤
+a≤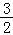 +a,即f(x)在区间[﹣
+a,即f(x)在区间[﹣ ,
,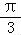 ]上的值域为[a,a+
]上的值域为[a,a+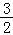 ],
],
又f(x)在区间[﹣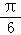 ,
,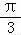 ]上的最大值与最小值的和为
]上的最大值与最小值的和为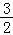 ,
,
∴a+a+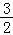 =
=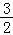 ,
,
解得a=0.
故答案是:π;0.
已知一个袋中装有大小相同的4个红球,3个白球,3个黄球.若任意取出2个球,则取出的2个球颜色相同的概率是 ;若有放回地任意取10次,每次取出一个球,每取到一个红球得2分,取到其它球不得分,则得分数X的方差为 .
知识点:9.离散型随机变量的分布列、均值与方差
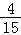 ,9.6.
,9.6.
【考点】离散型随机变量的期望与方差.
【分析】任意取出2个球,基本事件总数n=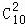 =45,取出的2个球颜色相同包含的基本事件个数m=
=45,取出的2个球颜色相同包含的基本事件个数m=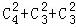 =12,由此能求出取出的2个球颜色相同的概率;有放回地任意取10次,每次取出一个球,每取到一个红球得2分,取到其它球不得分,取到红球的个数ξ~B(0.4,10),X=2ξ,由此能求出得分数X的方差.
=12,由此能求出取出的2个球颜色相同的概率;有放回地任意取10次,每次取出一个球,每取到一个红球得2分,取到其它球不得分,取到红球的个数ξ~B(0.4,10),X=2ξ,由此能求出得分数X的方差.
【解答】解:一个袋中装有大小相同的4个红球,3个白球,3个黄球.
任意取出2个球,基本事件总数n=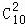 =45,
=45,
取出的2个球颜色相同包含的基本事件个数m=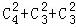 =12,
=12,
∴取出的2个球颜色相同的概率是p= .
.
∵有放回地任意取10次,每次取出一个球,每取到一个红球得2分,取到其它球不得分,
∴取到红球的个数ξ~B(0.4,10),
∴D(ξ)=10×0.4×0.6=2.4,
∵X=2ξ,
∴D(X)=4E(ξ)=4×2.4=9.6.
故答案为: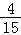 ,9.6.
,9.6.
已知x>0,y>0,xy=x+2y,则x+2y的最小值为 ;则xy的最小值为 .
知识点:4.基本不等式
8,8.
【考点】基本不等式.
【分析】直接利用基本不等式的性质即可得出.
【解答】解:x>0,y>0,xy=x+2y,∵x+2y≥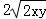 ,当且仅当x=2y时取等号.
,当且仅当x=2y时取等号.
即xy≥2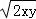
可得:(xy)2≥8xy,
∴xy≥8
∴xy的最小值为8.
同理:x+2y≥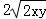 ,当且仅当x=2y时取等号.
,当且仅当x=2y时取等号.
∵xy≥8
∴x+2y≥8.
∴x+2y的最小值为8.
(1+2x2)(x﹣ )8的展开式中常数项为 .
)8的展开式中常数项为 .
知识点:3.二项式定理
﹣42
【考点】二项式定理的应用.
【分析】将问题转化成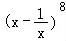 的常数项及含x﹣2的项,利用二项展开式的通项公式求出第r+1项,令x的指数为0,﹣2求出常数项及含x﹣2的项,进而相加可得答案.
的常数项及含x﹣2的项,利用二项展开式的通项公式求出第r+1项,令x的指数为0,﹣2求出常数项及含x﹣2的项,进而相加可得答案.
【解答】解:先求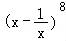 的展开式中常数项以及含x﹣2的项;
的展开式中常数项以及含x﹣2的项;

由8﹣2r=0得r=4,由8﹣2r=﹣2得r=5;
即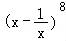 的展开式中常数项为C84,
的展开式中常数项为C84,
含x﹣2的项为C85(﹣1)5x﹣2
∴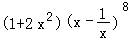 的展开式中常数项为C84﹣2C85=﹣42
的展开式中常数项为C84﹣2C85=﹣42
故答案为﹣42
若函数f(x)=|x+1|+2|x﹣a|的最小值为5,则实数a= .
知识点:12.绝对值函数与分段函数及其他函数
﹣6或4
【考点】带绝对值的函数.
【分析】分类讨论a与﹣1的大小关系,化简函数f(x)的解析式,利用单调性求得f(x)的最小值,再根据f(x)的最小值等于5,求得a的值.
【解答】解:∵函数f(x)=|x+1|+2|x﹣a|,故当a<﹣1时,f(x)=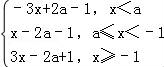 ,
,
根据它的最小值为f(a)=﹣3a+2a﹣1=5,求得a=﹣6.
当a=﹣1时,f(x)=3|x+1|,它的最小值为0,不满足条件.
当a≥﹣1时,f(x)=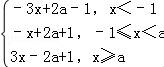 ,
,
根据它的最小值为f(a)=a+1=5,求得a=4.
综上可得,a=﹣6 或a=4,
故答案为:﹣6或4.
正方体ABCD﹣A1B1C1D1的棱长为2,MN是它的内切球的一条弦(把球面上任意两点之间的线段称为球的弦),P为正方体表面上的动点,当弦MN最长时. 的最大值为 .
的最大值为 .
知识点:8.空间向量及其运算
2
【考点】空间向量的数量积运算.
【分析】利用“当点P,M,N三点共线时,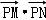 取得最大值”,此时
取得最大值”,此时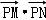 ≤
≤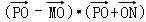 ,而
,而 ,可得
,可得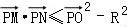 =
=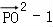 ,可知当且仅当点P为正方体的一个顶点时上式取得最大值,求出即可.
,可知当且仅当点P为正方体的一个顶点时上式取得最大值,求出即可.
【解答】解:设点O是此正方体的内切球的球心,半径R=1.
∵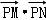
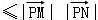 ,∴当点P,M,N三点共线时,
,∴当点P,M,N三点共线时,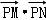 取得最大值.
取得最大值.
此时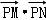 ≤
≤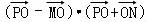 ,而
,而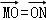 ,
,
∴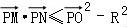 =
=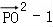 ,
,
当且仅当点P为正方体的一个顶点时上式取得最大值,
∴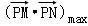 =
= =2.
=2.
故答案为2.
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费2元(不足1小时的部分按1小时计算).有甲、乙两人相互独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为 ,
, ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ,
, ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(Ⅰ)求甲乙两人所付的租车费用相同的概率.
(Ⅱ)设甲乙两人所付的租车费用之和为随机变量ξ,求ξ的分布列及数学期望Eξ.
知识点:9.离散型随机变量的分布列、均值与方差
【考点】离散型随机变量的期望与方差;互斥事件的概率加法公式.
【分析】(Ⅰ)首先求出两个人租车时间超过三小时的概率,甲乙两人所付的租车费用相同即租车时间相同:都不超过两小时、都在两小时以上且不超过三小时和都超过三小时三类求解即可.
(Ⅱ)随机变量ξ的所有取值为0,2,4,6,8,由独立事件的概率分别求概率,列出分布列,再由期望的公式求期望即可.
【解答】解:(Ⅰ)甲乙两人租车时间超过三小时的概率分别为: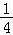 ,
,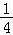
甲乙两人所付的租车费用相同的概率p=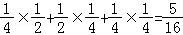
(Ⅱ)随机变量ξ的所有取值为0,2,4,6,8
P(ξ=0)=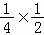 =
=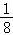
P(ξ=2)=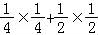 =
=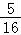
P(ξ=4)=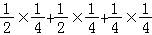 =
=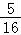
P(ξ=6)=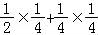 =
=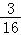
P(ξ=8)=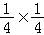 =
=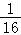
数学期望Eξ=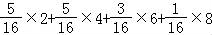 =
=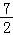
已知在递增等差数列{an}中,a1=2,a3是a1和a9的等比中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ,Sn为数列{bn}的前n项和,是否存在实数m,使得Sn<m对于任意的n∈N+恒成立?若存在,请求实数m的取值范围,若不存在,试说明理由.
,Sn为数列{bn}的前n项和,是否存在实数m,使得Sn<m对于任意的n∈N+恒成立?若存在,请求实数m的取值范围,若不存在,试说明理由.
知识点:2.等差数列及其性质
【考点】数列递推式;等差数列的通项公式.
【分析】(I)利用等差数列与等比数列的通项公式即可得出.
(Ⅱ)存在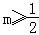 .由于bn=
.由于bn=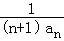 =
=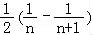 ,利用“裂项求和”方法即可得出.
,利用“裂项求和”方法即可得出.
【解答】解:(Ⅰ)由{an}为等差数列,设公差为d,则an=a1+(n﹣1)d,
∵a3是a1和a9的等比中项,
∴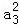 =a1•a9,即(2+2d)2=2(2+8d),
=a1•a9,即(2+2d)2=2(2+8d),
解得d=0(舍)或d=2,
∴an=2+2(n﹣1)=2n.
(Ⅱ)存在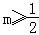 .
.
bn=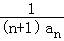 =
=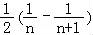 ,
,
∴数列{bn}的前n项和Sn=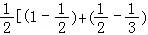 +…+
+…+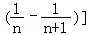 =
=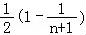
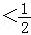 ,
,
∴存在实数m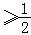 ,使得Sn<m对于任意的n∈N+恒成立.
,使得Sn<m对于任意的n∈N+恒成立.
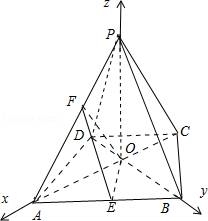
已知四棱锥P﹣ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,AB=2CD=2 ,E、F分别是AB、AP的中点.
,E、F分别是AB、AP的中点.
(1)求证:AC⊥EF;
(2)求二面角F﹣OE﹣A的余弦值.

知识点:10.空间角与距离
【考点】二面角的平面角及求法;直线与平面垂直的性质.
【分析】(1)通过建立空间直角坐标系,利用EF与AO的方向向量的数量积等于0,即可证明垂直;
(2)利用两个平面的法向量的夹角即可得到二面角的余弦值.
【解答】(1)证明:由ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,可知:△OAB是等腰直角三角形,
∵AB=2CD=2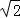 ,E是AB的中点,∴OE=EA=EB=
,E是AB的中点,∴OE=EA=EB=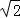 ,可得OA=OB=2.
,可得OA=OB=2.
∵PO⊥底面ABCD,∴PO⊥OA,PO⊥OB.又OA⊥OB.
∴可以建立如图所示的空间直角坐标系.
则O(0,0,0),A(2,0,0),B(0,2,0),P(0,0,2),E(1,1,0),F(1,0,1).
∴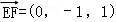 ,
,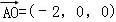 .
.
∴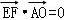 ,∴EF⊥AO,即EF⊥AC.
,∴EF⊥AO,即EF⊥AC.
(2)解:由(1)可知: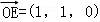 ,
,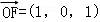 .
.
设平面OEF的法向量为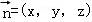 ,
,
则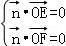 ,得
,得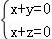 ,令x=1,则y=z=﹣1.
,令x=1,则y=z=﹣1.
∴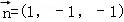 .
.
∵PO⊥平面OAE,∴可取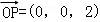 作为平面OAE的法向量.
作为平面OAE的法向量.
∴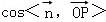 =
=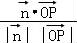 =
=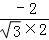 =
=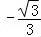 .
.
由图可知:二面角F﹣OE﹣A的平面角是锐角θ.
因此,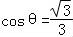 .
.
如图,在由圆O:x2+y2=1和椭圆C: =1(a>1)构成的“眼形”结构中,已知椭圆的离心率为
=1(a>1)构成的“眼形”结构中,已知椭圆的离心率为 ,直线l与圆O相切于点M,与椭圆C相交于两点A,B.
,直线l与圆O相切于点M,与椭圆C相交于两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,使得 •
• =
= ,若存在,求此时直线l的方程;若不存在,请说明理由.
,若存在,求此时直线l的方程;若不存在,请说明理由.

知识点:1.椭圆
【考点】直线与圆锥曲线的综合问题;平面向量数量积的运算;椭圆的标准方程.
【分析】(1)根据椭圆C: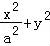 =1(a>1)的离心率为
=1(a>1)的离心率为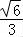 ,可得a2=3,从而可求椭圆C的方程;
,可得a2=3,从而可求椭圆C的方程;
(2)假设存在直线l,使得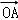 •
•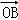 =
=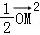 ,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,直线l代入椭圆C的方程为
,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,直线l代入椭圆C的方程为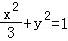 ,可得(1+3k2)x2+6kbx+3b2﹣3=0
,可得(1+3k2)x2+6kbx+3b2﹣3=0
设A(x1,y1)、B(x2,y2),进而利用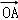 •
•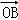 =
=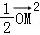 ,即可知存在直线l.
,即可知存在直线l.
【解答】解:(1)∵椭圆C: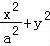 =1(a>1)的离心率为
=1(a>1)的离心率为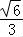 ,
,
∴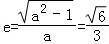
解得:a2=3,所以所求椭圆C的方程为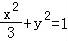
(2)假设存在直线l,使得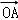 •
•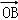 =
=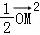 ,
,
当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,
由直线l与圆O相切,可得b2=k2+1 …(1)
直线ly=kx+b代入椭圆C的方程为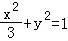 ,可得(1+3k2)x2+6kbx+3b2﹣3=0
,可得(1+3k2)x2+6kbx+3b2﹣3=0
设A(x1,y1)、B(x2,y2),则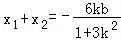 ,
,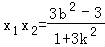
∴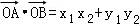 =
=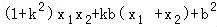 =
=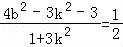 …(2)
…(2)
由(1)(2)可得k2=1,b2=2
故存在直线l,方程为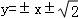 ,使得
,使得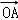 •
•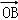 =
=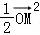 .
.
已知函数f(x)=lnx+ ,其中a为大于零的常数..
,其中a为大于零的常数..
(1)若函数f(x)在区间[1,+∞)内单调递增,求a的取值范围;
(2)求函数f(x)在区间[1,2]上的最小值;
(3)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 成立.
成立.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.
【分析】(1)求导,将函数f(x)在区间[1,+∞)上单调递增化为导数恒不小于0,从而求a的取值范围;
(2)研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最小值.
(3)由(1)知函数f(x)=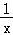 ﹣1+lnx在[1,+∞)上为增函数,构造n与n﹣1的递推关系,可利用叠加法求出所需结论
﹣1+lnx在[1,+∞)上为增函数,构造n与n﹣1的递推关系,可利用叠加法求出所需结论
【解答】解:(1)由题意,f′(x)=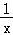 ﹣
﹣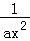 =
=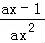 ,
,
∵a为大于零的常数,
若使函数f(x)在区间[1,+∞)上单调递增,
则使ax﹣1≥0在区间[1,+∞)上恒成立,
即a﹣1≥0,
故a≥1;(2)当a≥1时,f′(x)>0在(1,2)上恒成立,
这时f(x)在[1,2]上为增函数∴f(x)min=f(1)=0.
当0<a≤ ,∵f′(x)<0在(1,2)上恒成立,
,∵f′(x)<0在(1,2)上恒成立,
这时f(x)在[1,2]上为减函数∴f(x)min=f(2)=ln2﹣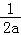 ,
,
当 <a<1时,令f′(x)=0,得x=
<a<1时,令f′(x)=0,得x=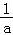 ∈(1,2).
∈(1,2).
又∵对于x∈[1,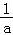 )有f′(x)<0,
)有f′(x)<0,
对于x∈(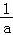 ,2]有f′(x)>0,
,2]有f′(x)>0,
∴f(x)min=f(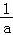 )=ln
)=ln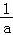 +1﹣
+1﹣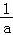 ,
,
综上,f(x)在[1,2]上的最小值为
①当0<a≤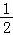 时,f(x)min=ln2﹣
时,f(x)min=ln2﹣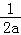 ;
;
②当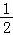 <a<1时,f(x)min=ln
<a<1时,f(x)min=ln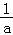 +1﹣
+1﹣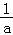 .
.
③当a≥1时,f(x)min=0;
(3)由(1)知函数f(x)=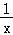 ﹣1+lnx在[1,+∞)上为增函数,
﹣1+lnx在[1,+∞)上为增函数,
当n>1时,∵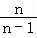 >1,∴f(
>1,∴f(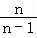 )>f(1),
)>f(1),
即lnn﹣ln(n﹣1)>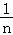 ,对于n∈N*且n>1恒成立.
,对于n∈N*且n>1恒成立.
lnn=[lnn﹣ln(n﹣1)]+[ln(n﹣1)﹣ln(n﹣2)]++[ln3﹣ln2]+[ln2﹣ln1]>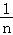 +
+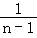 +…+
+…+ ,
,
∴对于n∈N*,且n>1时,lnn> +
+ +…+
+…+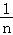 恒成立.
恒成立.