国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了![]() 元助学贷款,并承诺在毕业后
元助学贷款,并承诺在毕业后![]() 年内(按
年内(按![]() 个月计)全部还清.签约的单位提供的工资标准为第一年内每月
个月计)全部还清.签约的单位提供的工资标准为第一年内每月![]() 元,第
元,第![]() 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加![]() 直到
直到![]() 元.凌霄同学计划前
元.凌霄同学计划前![]() 个月每个月还款额为
个月每个月还款额为![]() ,第
,第![]() 个月开始,每月还款额比上一月多
个月开始,每月还款额比上一月多![]() 元.(Ⅰ)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求
元.(Ⅰ)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求![]() 的值;(Ⅱ)当
的值;(Ⅱ)当![]() 时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月
时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月![]() 元的基本生活费?
元的基本生活费?
(参考数据:![]() )
)
知识点:14.函数的应用问题
解:(Ⅰ)依题意,从第13个月开始,每月还款额比前一个月多![]() 元,故
元,故
![]()
即 ![]() ,解得
,解得![]() (元).
(元).
即要使在三年全部还清,第13个月起每个月必须比上一个月多还![]() 元.
元.
(Ⅱ)设凌霄第![]() 个月还清,则应有
个月还清,则应有
![]()
即![]() ,解之得
,解之得![]() ,取
,取![]() .
.
即凌霄工作![]() 个月就可以还清贷款.
个月就可以还清贷款.
这个月凌霄的还款额为
![]() 元
元
第31个月凌霄的工资为![]() 元.
元.
因此,凌霄的剩余工资为![]() ,能够满足当月的基本生活需求.
,能够满足当月的基本生活需求.
解法2:(Ⅰ)依题意,从第13个月开始,每个月的还款额为![]() 构成等差数列,其中
构成等差数列,其中![]() ,公差为
,公差为![]() . 从而,到第
. 从而,到第![]() 个月,凌霄共还款
个月,凌霄共还款![]()
令![]() ,解之得
,解之得![]() (元).
(元).
即要使在三年全部还清,第13个月起每个月必须比上一个月多还![]() 元.
元.
(Ⅱ)设凌霄第![]() 个月还清,则应有
个月还清,则应有
![]()
整理可得![]() ,解之得
,解之得![]() ,取
,取![]() .
.
即凌霄工作![]() 个月就可以还清贷款.
个月就可以还清贷款.
这个月凌霄的还款额为
![]() 元
元
第31个月凌霄的工资为![]() 元.
元.
因此,凌霄的剩余工资为![]() ,能够满足当月的基本生活需求.
,能够满足当月的基本生活需求.
如图,抛物线![]() 与双曲线
与双曲线![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() 在第一象限的交点,且
在第一象限的交点,且![]() .(Ⅰ)求双曲线
.(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)以![]() 为圆心的圆
为圆心的圆![]() 与双曲线的一条渐近线相切,
与双曲线的一条渐近线相切,
圆![]() :
:![]() .已知点
.已知点![]() ,过点
,过点![]() 作互相垂
作互相垂
直且分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 截得
截得
的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
. ![]() 是否为定值?请说明理由.
是否为定值?请说明理由.

知识点:3.抛物线
解:(Ⅰ)∵抛物线![]() 的焦点为
的焦点为![]() ,
,
∴双曲线![]() 的焦点为
的焦点为![]() 、
、![]() ,
,
设![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,
,
由抛物线的定义得,![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵点![]() 在双曲线上,由双曲线定义得,
在双曲线上,由双曲线定义得,![]() ,∴
,∴![]() , ∴双曲线的方程为:
, ∴双曲线的方程为:![]() .
.
(Ⅱ)![]() 为定值.下面给出说明.设圆
为定值.下面给出说明.设圆![]() 的方程为:
的方程为:![]() ,双曲线的渐近线方程为:
,双曲线的渐近线方程为:![]() ,
,
∵圆![]() 与渐近线
与渐近线![]() 相切,∴圆
相切,∴圆![]() 的半径为
的半径为 ,
,
故圆![]() :
:![]() ,
,
设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长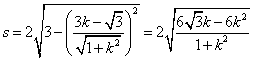 ,
,
直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长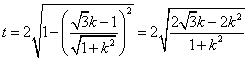 ,
,
∴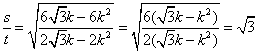 ,故
,故![]() 为定值
为定值![]() .
.
设曲线![]() 在点
在点![]() 处的切线与y轴交于点
处的切线与y轴交于点![]() .
.
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,猜测
,猜测![]() 的最大值并证明你的结论.
的最大值并证明你的结论.
知识点:3.数列
解:(Ⅰ)![]() ,
,
∴点P处的切线斜率![]() ,
∴切线方程为:
,
∴切线方程为:![]() ,
,
令![]() 得:
得: ![]() ,故数列
,故数列![]() 的通项公式为:
的通项公式为:![]() .
.
(2) ![]() ------①
------①
两边同乘![]() 得:
得:![]() ------②
------②
①![]() ②得:
②得: ![]()
![]()

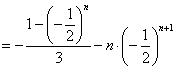
∴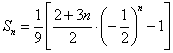
其中![]() ,
, ![]() ,
,![]() ,
,![]()
猜测![]() 的最大值为
的最大值为![]() .证明如下:
.证明如下:
(i)当![]() 为奇数时,
为奇数时,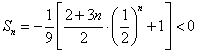 ;
;
(ii)当![]() 为偶数时,
为偶数时,![]() ,设
,设![]() ,则
,则![]() .
.
![]() , ∴
, ∴![]() .
.
故![]() 的最大值为
的最大值为![]() ,即
,即![]() 的最大值为
的最大值为![]() .
.
解法2 (2)任意![]() ,都有
,都有![]() ;所以
;所以![]() 的最大值就是
的最大值就是![]() 的最大值.
的最大值.
令![]() ,显然
,显然![]() ,
,
所以![]() 的最大值是
的最大值是![]() .
.
已知二次函数![]() (
(![]() )的导函数的图象如图所示:
)的导函数的图象如图所示:
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)令![]() ,求
,求![]() 在
在![]() 上的最大值.
上的最大值.
知识点:15.函数的图像
解析:(Ⅰ)因为![]() ,由图可知,
,由图可知,![]() ,
,
∴![]() ,得
,得![]() ,故所求函数解析式为
,故所求函数解析式为![]() .
.
(Ⅱ)![]() ,则
,则![]() .
.
法一:①若![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,故
上是增函数,故![]() .
.
②若![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
∵![]() ,
,![]() ,∴当
,∴当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
③若![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是减函数,故
上是减函数,故![]() .
.
综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
法二:![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
∴当![]() 或
或![]() 时,
时,![]() 取得最大值,其中
取得最大值,其中![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
在平面直角坐标系中,已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的切线,其切点分别为
的切线,其切点分别为![]() 、
、![]() (其中
(其中![]() ).(Ⅰ)求
).(Ⅰ)求![]() 与
与![]() 的值;(Ⅱ)若以点
的值;(Ⅱ)若以点![]() 为圆心的圆
为圆心的圆![]() 与直线
与直线![]() 相切,求圆
相切,求圆![]() 的面积;(Ⅲ)过原点
的面积;(Ⅲ)过原点![]() 作圆
作圆![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
知识点:3.抛物线
解析:(Ⅰ)由![]() 可得,
可得,![]() .
.
∵直线![]() 与曲线
与曲线![]() 相切,且过点
相切,且过点![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,或
,或![]() ,同理可得:
,同理可得:![]() ,或
,或![]()
∵![]() ,∴
,∴![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() ,则直线
,则直线![]() 的斜率
的斜率![]() ,
,
∴直线![]() 的方程为:
的方程为:![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() .
.
∵点![]() 到直线
到直线![]() 的距离即为圆
的距离即为圆![]() 的半径,即
的半径,即![]() ,
,
故圆![]() 的面积为
的面积为![]() .
.
(Ⅲ)四边形![]() 的面积为
的面积为![]() 不妨设圆心
不妨设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,垂足为
,垂足为![]() ;圆心
;圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,垂足为
,垂足为![]() ;则
;则![]()
由于四边形![]() 为矩形.且
为矩形.且![]()
所以![]()
由基本不等式![]() 可得
可得
![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
已知点列![]()
![]() 顺次为直线
顺次为直线![]() 上的点,点列
上的点,点列![]()
![]() 顺次为
顺次为![]() 轴上的点,其中
轴上的点,其中![]()
![]() ,对任意的
,对任意的![]() ,点
,点![]() 、
、![]() 、
、![]() 构成以
构成以![]() 为顶点的等腰三角形.(Ⅰ)求证:对任意的
为顶点的等腰三角形.(Ⅰ)求证:对任意的![]() ,
,![]() 是常数,并求数列
是常数,并求数列![]() 的通项公式;(Ⅱ)问是否存在等腰直角三角形
的通项公式;(Ⅱ)问是否存在等腰直角三角形![]() ?请说明理由.
?请说明理由.
知识点:3.分类与整合思想
解:(Ⅰ)由题意得![]() ,
,![]() ,
,![]() ,
,
∵点![]() 、
、![]() 、
、![]() 构成以
构成以![]() 为顶点的等腰三角形,
为顶点的等腰三角形,
∴![]() ,即
,即![]()
得![]()
又∵![]() ,∴
,∴![]() , ①
则
, ①
则![]() ②
②
由②-①得,![]() ,即
,即![]() 是常数.即所列
是常数.即所列![]() 都是等差数列.
都是等差数列.
(注:可以直接由图像得到![]() ,即
,即![]() , (
, (![]() ) )
) )
当![]() 为正奇数时,
为正奇数时,![]() ,
,
当![]() 为正偶数时,由
为正偶数时,由![]() 得,
得,![]() ,故
,故![]() ,
,
∴![]() .
.
(Ⅱ)假设存在等腰直角三角形![]() ,由题意
,由题意![]() .
.
在![]() 中,
中,![]() .
.
当![]() 为正奇数时,
为正奇数时,![]() ,
,![]() ,
,
∴![]() ,故有
,故有![]() ,即
,即![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴当![]() 时,使得三角形
时,使得三角形![]() 为等腰直角三角形.
为等腰直角三角形.
当![]() 为正偶数时,
为正偶数时,![]() ,
,![]() ,
,
∴![]() ,故有
,故有![]() ,即
,即![]() ,
,
又∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴当![]() 时,使得三角形
时,使得三角形![]() 为等腰直角三角形.
为等腰直角三角形.
综上所述,当![]() 时,使得三角形
时,使得三角形![]() 为等腰直角三角形.
为等腰直角三角形.
注:也可以回答为![]() 时,使得三角形
时,使得三角形![]() 为等腰直角三角形.
为等腰直角三角形.
已知动点![]() 到定点
到定点![]() 的距离与点
的距离与点![]() 到定直线
到定直线![]() :
:![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 、
、![]() 是直线
是直线![]() 上的两个点,点
上的两个点,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,若
对称,若![]() ,求
,求![]() 的最小值.
的最小值.
知识点:10.圆锥曲线与方程
(1)解:设点![]() ,依题意,有
,依题意,有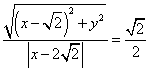 . 整理,得
. 整理,得![]() .
.
所以动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)解:∵点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,∴点
对称,∴点![]() 的坐标为
的坐标为![]() .
.
∵![]() 、
、![]() 是直线
是直线![]() 上的两个点,∴可设
上的两个点,∴可设![]() ,
,![]() (不妨设
(不妨设![]() ).
).
∵![]() ,∴
,∴![]() .即
.即![]() .即
.即![]() .
.
由于![]() ,则
,则![]() ,
,![]() . ∴
. ∴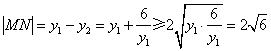 .
.
当且仅当![]() ,
,![]() 时,等号成立.故
时,等号成立.故![]() 的最小值为
的最小值为![]() .
.
已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,函数
上是增函数,函数![]() 在
在![]() 上有三个零点,且1是其中一个零点.(1)求
上有三个零点,且1是其中一个零点.(1)求![]() 的值; (2)求
的值; (2)求![]() 的取值范围;(3)试探究直线
的取值范围;(3)试探究直线![]() 与函数
与函数![]() 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
知识点:2.函数概念与基本初等函数Ⅰ
(1)解:∵![]() ,∴
,∴![]() .
.
∵![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴当![]() 时,
时,![]() 取到极小值,即
取到极小值,即![]() . ∴
. ∴![]() .
.
(2)解:由(1)知,![]() , ∵1是函数
, ∵1是函数![]() 的一个零点,即
的一个零点,即![]() ,∴
,∴![]() .
.
∵![]() 的两个根分别为
的两个根分别为![]() ,
,![]() .
.
∵![]() 在
在![]() 上是增函数,且函数
上是增函数,且函数![]() 在
在![]() 上有三个零点,∴
上有三个零点,∴![]() ,即
,即![]() .
.
∴![]() .故
.故![]() 的取值范围为
的取值范围为![]() .
.
(3)解:由(2)知![]() ,且
,且![]() .
.
要讨论直线![]() 与函数
与函数![]() 图像的交点个数情况,
图像的交点个数情况,
即求方程组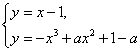 解的个数情况.
解的个数情况.
由![]() ,得
,得![]() .
.
即![]() .
.
即![]() .∴
.∴![]() 或
或![]() .
.
由方程![]() , (*)
得
, (*)
得![]() .
.
∵![]() ,若
,若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)无实数解.
.此时方程(*)无实数解.
若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)有一个实数解
.此时方程(*)有一个实数解![]() .
.
若![]() ,即
,即![]() ,解得
,解得![]() .此时方程(*)有两个实数解,分别为
.此时方程(*)有两个实数解,分别为![]() ,
,![]() .且当
.且当![]() 时,
时,![]() ,
,![]() .
.
综上所述,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有一个交点.
的图像有一个交点.
当![]() 或
或![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有二个交点.
的图像有二个交点.
当![]() 且
且![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图像有三个交点.
的图像有三个交点.
已知数列![]() 满足对任意的
满足对任意的![]() ,都有
,都有![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;(2)求数列
的值;(2)求数列![]() 的通项公式
的通项公式![]() ;(3)设数列
;(3)设数列 的前
的前![]() 项和为
项和为![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
知识点:3.数列
(1)解:当![]() 时,有
时,有![]() ,由于
,由于![]() ,所以
,所以![]() .
.
当![]() 时,有
时,有![]() ,将
,将![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由于![]() ,
①
,
①
则有![]() .
②
.
②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() .
③
.
③
同样有![]()
![]() ,
④
,
④
③-④,得![]() . 所以
. 所以![]() .由于
.由于![]() ,即当
,即当![]() 时都有
时都有![]() ,
,
所以数列![]() 是首项为1,公差为1的等差数列.故
是首项为1,公差为1的等差数列.故![]() .
.
(3)解:由(2)知![]() ,则
,则![]() .
.
所以![]()
![]()
![]()
![]() .
.
∵![]() ,∴数列
,∴数列![]() 单调递增.所以
单调递增.所以![]() .
.
要使不等式![]() 对任意正整数
对任意正整数![]() 恒成立,只要
恒成立,只要![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() ,即
,即![]() .所以,实数
.所以,实数![]() 的取值范围是
的取值范围是![]() .
.
已知椭圆的一个顶点为![]() ,焦点在
,焦点在![]() 轴上.若右焦点到直线
轴上.若右焦点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆的标准方程;(2)设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() .当
.当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
知识点:1.椭圆
解:(1)依题意可设椭圆方程为 ![]() ,则右焦点
,则右焦点![]()
由题设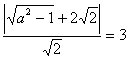 ,解得
,解得![]() ,故所求椭圆的方程为
,故所求椭圆的方程为![]()
(2)设![]() ,设P为弦MN的中点,
,设P为弦MN的中点,
由 得
得 ![]() ,
,![]() 直线与椭圆相交,
直线与椭圆相交,
![]()
![]() ,①
,①
![]() 从而
从而![]() ,
,
![]() 又
又![]() ,则
,则
![]() 即
即 ![]() , ② …………………………10分
, ② …………………………10分
把②代入①得 ![]() 解得
解得 ![]() , 由②得
, 由②得 ![]() 解得
解得![]() .
.
综上求得![]() 的取值范围是
的取值范围是![]() .
.
已知函数![]()
![]()
![]() 的图象上。(1)求数列
的图象上。(1)求数列![]() 的通项公式
的通项公式![]() ;(2)令
;(2)令![]() 求数列
求数列![]() (3)令
(3)令![]() 证明:
证明:![]() .
.
知识点:2.函数概念与基本初等函数Ⅰ
解:(1)![]()
当![]() ;当
;当![]() ,适合上式,
,适合上式,![]()
(2)![]() ,
,![]() ①
①
![]() ,
②
,
②
由①![]() ②得:
②得:![]()
![]()
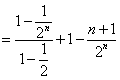 =
=![]() ,
,![]()
(3)证明:由![]()
![]() 又
又![]()
![]() ……12分
……12分
![]() ,
,![]() 成立
成立