给定公比为
q ( q≠ 1)的等比数列{ a n },设 b 1 =
a 1 + a 2 + a 3 , b 2
= a 4 + a 5 + a 6 ,…, b n = a 3 n -2 + a 3
n -1 + a 3 n ,…,则数列{ b n }( )
( A )是等差数列
(
B )是公比为 q 的等比数列
( C )是公比为 q 3
的等比数列 ( D )既非等差数列也非等比数列
知识点:4.等比数列及其性质
C
由题设,an=a1qn-1 ,则
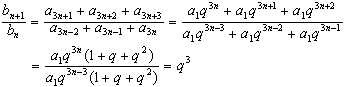
因此,{bn}是公比为q3的等比数列.
平面直角坐标系中,纵、横坐标都是整数的点叫做整点,那么,满足不等式 (| x |-1) 2 +(| y |-1) 2 <2的整点( x , y )的个数是( )
( A )16 ( B )17 (
C )18 ( D )25
知识点:3.二元一次不等式(组)与简单的线性规划
A
由(|x|-1)2+(|y|-1)2<2,可得(|x|-1,|y|-1)为(0,0),(0,1),(0,-1),(1,0)或(-1,0).从而,不难得到(x,y)共有16个.
若(log23)x-(log53)x ≥(log23)-y-(log53)-y,则(
)
( A ) x - y ≥0
( B ) x + y ≥0
( C ) x - y ≤0 ( D ) x + y ≤0
知识点:16函数值的大小比较
B
记f(t)=(log23)t-(log53)t,则f(t)在R上是严格增函数.原不等式即f(x)≥f(-y).
故x≥-y,即x+y≥0.
给定下列两个关于异面直线的命题:
命题Ⅰ:若平面 α 上的直线 a 与平面 β 上的直线
b 为异面直线,直线 c 是 α
与β 的交线,那么, c 至多与 a , b 中的一条相交;
命题Ⅱ:不存在这样的无穷多条直线,它们中的任意两条都是异面直线。
那么,( )
( A )命题Ⅰ正确,命题Ⅱ不正确
( B )命题Ⅱ正确,命题Ⅰ不正确
( C )两个命题都正确
( D )两个命题都不正确
知识点:4.空间点、直线、平面之间的位置关系
D
如图,c与a、b都相交;故命题Ⅰ不正确;又可以取无穷多个平行平面,在每个平面上取一条直线,且使这些直线两两不同向,则这些直线中的任意两条都是异面直线,从而命题Ⅱ也不正确.
在某次乒乓球单打比赛中,原计划每两名选手恰比赛一场,但有3名选手各比赛了2场之后就退出了,这样,全部比赛只进行了50场。那么,在上述3名选手之间比赛的场数是( )
( A )0 ( B )1 (
C )2 ( D )3
知识点:1.两个计数原理
B
设这三名选手之间的比赛场数是r,共n名选手参赛.由题意,可得 ![]() ,即
,即 ![]() =44+r.由于0≤r≤3,经检验可知,仅当r=1时,n=13为正整数.
=44+r.由于0≤r≤3,经检验可知,仅当r=1时,n=13为正整数.
已知点 A (1,2),过点(5,-2)的直线与抛物线 y 2 =4
x 交于另外两点 B , C
,那么,△ ABC 是(
)
( A )锐角三角形
( B )钝角三角形
( C )直角三角形 ( D )答案不确定
知识点:4.直线与圆锥曲线的位置关系
C
设B(t2,2t),C(s2,2s),s≠t,s≠1,t≠1,则直线BC的方程为 ![]() ,化得2x-(s+t)y+2st=0.
,化得2x-(s+t)y+2st=0.
由于直线BC过点(5,-2),故 2×5-(s+t)(-2)+2st=0,即 (s+1)(t+1)=-4.
因此, ![]() .
.
所以,∠BAC=90°,从而△ABC是直角三角形.
已知正整数 n 不超过2000,并且能表示成不少于60个连续正整数之和,那么,这样的 n 的个数是___________.
知识点:3.分类与整合思想
6
首项为a为的连续k个正整数之和为
![]() .
.
由Sk≤2000,可得60≤k≤62.
当k=60时,Sk=60a+30×59,由Sk≤2000,可得a≤3,故Sk=1830,1890,1950;
当k=61时,Sk=61a+30×61,由Sk≤2000,可得a≤2,故Sk=1891,1952;
当k=62时,Sk=62a+31×61,由Sk≤2000,可得a≤1,故Sk=1953.
于是,题中的n有6个.
复数(12+5i)2(239-i)的辐角主值是_________.
知识点:2.复数的几何意义
![]()
z的辐角主值
argz=arg[(12+5i)2(239-i)]
=arg[(119+120i)(239-i)]
=arg[28561+28561i]=![]() .
.
在△
ABC 中,记 BC = a , CA = b , AB = c ,若9 a 2 +9 b
2 -19 c 2 =0,则![]() =__________.
=__________.
知识点:9.正弦定理和余弦定理(解三角形)
![]()
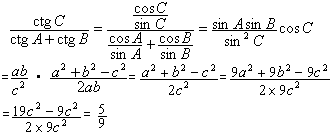
已知点
P 在双曲线![]() 上,并且 P 到这条双曲线的右准线的距离恰是 P 到这条双曲线的两个焦点的距离的等差中项,那么,
P 的横坐标是_____.
上,并且 P 到这条双曲线的右准线的距离恰是 P 到这条双曲线的两个焦点的距离的等差中项,那么,
P 的横坐标是_____.
知识点:2.双曲线
![]()
记半实轴、半虚轴、半焦距的长分别为a、b、c,离心率为e,点P到右准线l的距离为d,则a=4, b=3, c=5, ![]() , 右准线l为
, 右准线l为![]() .
.
如果P在双曲线右支,则
|PF1|=|PF2|+2a=ed+2a.
从而,
|PF1|+|PF2|=(ed+2a)+ed=2ed+2a>2d,
这不可能;故P在双曲线的左支,则
|PF2|-|PF1|=2a,|PF1|+|PF2|=2d.
两式相加得2|PF2|=2a+2d.
又|PF2|=ed,从而ed=a+d.
故 ![]() .
.
因此,P的横坐标为![]() .
.
已知直线![]() 中的 a
, b , c 是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是______.
中的 a
, b , c 是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是______.
知识点:1.直线的倾斜角、斜率与方程
43
设倾斜角为θ,则tgθ=-![]() >0.不妨设a>0,则b<0.
>0.不妨设a>0,则b<0.
(1)c=0,a有三种取法,b有三种取法,排除2个重复(3x-3y=0,2x-2y=0与x-y=0为同一直线),故这样的直线有3×3-2=7条;
(2)c≠0,则a有三种取法,b有三种取法,c有四种取法,且其中任两条直线均不相同,故这样的直线有3×3×4=36条.
从而,符合要求的直线有7+36=43条.
已知三棱锥
S - ABC 的底面是正三角形,
A 点在侧面 SBC 上的射影 H 是△ SBC 的垂心,二面角 H - AB - C 的平面角等于30°, SA =2 ![]() 。那么三棱锥 S - ABC 的体积为__________.
。那么三棱锥 S - ABC 的体积为__________.
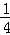
知识点:3.空间几何体的表面积与体积
![]()
由题设,AH⊥面SBC.作BH⊥SC于E.由三垂线定理可知SC⊥AE,SC⊥AB.故SC⊥面ABE.设S在面ABC内射影为O,则SO⊥面ABC.由三垂线定理之逆定理,可知CO⊥AB于F.同理,BO⊥AC.故O为△ABC的垂心.
又因为△ABC是等边三角形,故O为△ABC的中心,从而SA=SB=SC=![]() .
.
因为CF⊥AB,CF是EF在面ABC上的射影,由三垂线定理,EF⊥AB. 所以,∠EFC是二面角H-AB-C的平面角.故∠EFC=30°,
OC=SCcos60°=![]() ,
,
SO=![]() tg60°=
tg60°=![]() ×
×![]() =3.
=3.
又 OC=![]() AB,故AB=
AB,故AB=![]() OC=
OC=![]() ×
×![]() =3.
=3.
所以,VS-ABC=![]() .
.
已知当 x ∈[0,1]时,不等式
x2cosθ-x(1-x)+(1-x)2sinθ>0,恒成立,试求θ的取值范围。
知识点:5.三角函数的求值、化简与证明
若对一切x∈[0,1],恒有 f(x)=x2cosθ-x(1-x)+(1-x)2sinθ>0,
则
cosθ=f(1)>0,sinθ=f(0)>0. (1)
取 x0= ![]() ∈(0,1),则
∈(0,1),则 ![]() .
.
由于 ![]() +2
+2![]() x(1-x),
x(1-x),
所以,0<f(x0)=2![]() x0(1-x0) .
x0(1-x0) .
故 -![]() +
+![]() >0 (2)
>0 (2)
反之,当(1),(2)成立时,f(0)=sinθ>0,f(1)=cosθ>0,且x∈(0,1)时,f(x)≥2![]() x(1-x)>0.
x(1-x)>0.
先在[0,2π]中解(1)与(2):
由cosθ>0,sinθ>0,可得0<θ<![]() .
.
又-![]() +
+![]() >0,
>0,![]() >
>![]() ,
,
![]() sin2θ>
sin2θ>![]() , sin2θ>
, sin2θ>![]() ,
,
注意到 0<2θ<π,故有 ![]() <2θ<
<2θ<![]() ,
,
所以,![]() <θ<
<θ<![]() .
.
因此,原题中θ的取值范围是 2kπ+![]() <θ<2kπ+
<θ<2kπ+![]() ,k∈Z.
,k∈Z.
给定
A (-2,2),已知 B 是椭圆![]() 上的动点, F 是左焦点,当| AB |+
上的动点, F 是左焦点,当| AB |+ ![]() | BF |取最小值时,求 B 的坐标。
| BF |取最小值时,求 B 的坐标。
知识点:1.椭圆
记椭圆的半长轴、半短轴、半焦距分别为a、b、c,离心率为e.则a=5,b=4,c=![]() =
=![]() =3,e=
=3,e=![]() =
=![]() ,左准线为x=-
,左准线为x=-![]() .
.
过点B作左准线x=-![]() 的垂线,垂足为N,过A作此准线的垂线,垂足为M.由椭圆定义,
的垂线,垂足为N,过A作此准线的垂线,垂足为M.由椭圆定义,
|BN|=![]() =
=![]() |BF| .
|BF| .
于是, |AB|+![]() |BF|=|AB|+|BN|≥|AN|≥|AM|(定值),等号成立当且仅当B是AM与椭圆的交点时,此时B(
|BF|=|AB|+|BN|≥|AN|≥|AM|(定值),等号成立当且仅当B是AM与椭圆的交点时,此时B(![]() ,2)
,2)
所以,当|AB|+![]() |BF|取最小值时,B的坐标为(
|BF|取最小值时,B的坐标为(![]() ,2).
,2).