已知集合A={x|x=2k﹣1,k∈Z},B={x| ≤0},则A∩B=( )
≤0},则A∩B=( )
A.[﹣1,3] B.{﹣1,3} C.{﹣1,1} D.{﹣1,1,3}
知识点:3.集合的基本运算
C
【考点】交集及其运算.
【专题】集合.
【分析】求出B中不等式的解集确定出B,由A为奇数集,求出A与B的交集即可.
【解答】解:由B中不等式变形得:(x+1)(x﹣3)≤0,且x﹣3≠0,
解得:﹣1≤x<3,即B=[﹣1,3),
∵A为奇数集合,
∴A∩B={﹣1,1},
故选:C.
【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
若a、b、c为实数,则下列命题正确的是( )
A.若a>b,则ac2>bc2 B.若a<b<0,则a2>ab>b2
C.若a<b,则 >
> D.若a>b>0,则
D.若a>b>0,则 >
>
知识点:1.不等式关系与不等式
B
【考点】不等式的基本性质.
【专题】不等式的解法及应用.
【分析】A.c=0时不成立;
B.利用不等式的基本性质由a<b<0,可得a2>ab>b2;
C.取a=﹣1,b=﹣2时,即可判断出;
D.由a>b>0,可得 <
<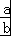 .
.
【解答】解:A.c=0时不成立;
B.∵a<b<0,∴a2>ab>b2,正确;
C.取a=﹣1,b=﹣2时, =﹣1,
=﹣1,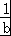 =﹣
=﹣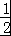 ,则
,则 >
>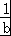 不成立;
不成立;
D.若a>b>0,则 <
<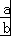 ,因此不正确.
,因此不正确.
故选:B.
【点评】本题考查了基本不等式的性质,考查了推理能力,属于基础题.
已知t∈R,i为虚数单位,复数z1=3+4i,z2=t+i,且z1•z2是实数,则t等于( )
A. B.
B. C.﹣
C.﹣ D.﹣
D.﹣
知识点:3.复数代数形式的四则运算
D
【考点】复数代数形式的混合运算.
【专题】数系的扩充和复数.
【分析】直接利用复数的乘法运算法则,复数是实数,虚部为0求解即可.
【解答】解:t∈R,i为虚数单位,复数z1=3+4i,z2=t+i,且z1•z2是实数,
可得(3+4i)(t+i)=3t﹣4+(4t+3)i,
4t+3=0
则t=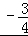 .
.
故选:D.
【点评】本题考查复数的基本知识,复数的概念的应用,考查计算能力.
设等差数列{an}的前n项为Sn,已知a1=﹣11,a3+a7=﹣6,当Sn取最小值时,n=( )
A.5 B.6 C.7 D.8
知识点:3.等差数列的前n项和
B
【考点】等差数列的前n项和.
【专题】等差数列与等比数列.
【分析】由等差数列的性质和题意求出a5的值,再求出公差d、an和Sn,对Sn化简后利用二次函数的性质,求出Sn取最小值时对应的n的值.
【解答】解:由等差数列的性质得,2a5=a3+a7=﹣6,
则a5=﹣3,
又a1=﹣11,所以d=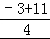 =2,
=2,
所以an=a1+(n﹣1)d=2n﹣13,
Sn=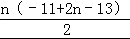 =n2﹣12n,
=n2﹣12n,
所以当n=6时,Sn取最小值,
故选:B.
【点评】本题考查等差数列的性质、通项公式,以及利用二次函数的性质求Sn最小值的问题.
△ABC中,∠C=90°,CA=CB=2,点M在边AB上,且满足 =3
=3 ,则
,则 •
• =( )
=( )
A. B.1 C.2 D.
B.1 C.2 D.
知识点:4.平面向量的数量积(夹角、模)
B
【考点】平面向量数量积的运算.
【专题】平面向量及应用.
【分析】由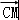 •
•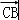 =(
=(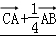 )•
)•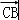 ,再利用向量
,再利用向量 和
和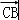 的夹角等于45°,两个向量的数量积的定义,求出
的夹角等于45°,两个向量的数量积的定义,求出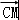 •
•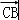 的值.
的值.
【解答】解:由题意得 AB=2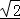 ,△ABC是等腰直角三角形,
,△ABC是等腰直角三角形,
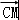 •
•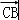 =(
=(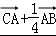 )•
)•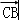 =0+
=0+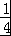
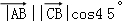 =
=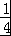 ×
×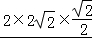 =1.
=1.
故选B.
【点评】本题考查两个向量的数量积的定义,注意向量 和
和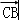 的夹角等于45°这一条件的运用.
的夹角等于45°这一条件的运用.
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )

A. B.
B. C.
C. D.
D.
知识点:10.对数函数及其性质
B
【考点】对数函数的图像与性质;指数函数的图像变换.
【专题】函数的性质及应用.
【分析】由图象可知对数的底数满足0<a<1,且0<f(0)<1,再根据指数函数g(x)=ax+b的性质即可推得.
【解答】解:由图象可知0<a<1且0<f(0)<1,
即 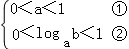 即
即
解②得loga1<logab<logaa,
∵0<a<1∴由对数函数的单调性可知a<b<1,
结合①可得a,b满足的关系为0<a<b<1,
由指数函数的图象和性质可知,g(x)=ax+b的图象是单调递减的,且一定在x轴上方.
故选:B.
【点评】本小题主要考查对数函数的图象、指数函数的图象、对数函数的图象的应用、方程组的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于基础题.
若实数x,y满足不等式组 ,则目标函数z=x﹣2y的最大值是( )
,则目标函数z=x﹣2y的最大值是( )
A.1 B.2 C.3 D.4
知识点:3.二元一次不等式(组)与简单的线性规划
A
【考点】简单线性规划.
【专题】数形结合;不等式的解法及应用.
【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,求得最优解的坐标,代入目标函数得答案.
【解答】解:由约束条件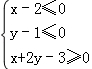 作出可行域如图,
作出可行域如图,
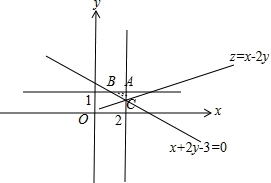
化目标函数z=x﹣2y为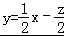 ,
,
由图可知,当直线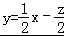 过C(2,
过C(2,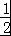 )时,直线在y轴上的截距直线,z最大.
)时,直线在y轴上的截距直线,z最大.
∴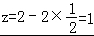 .
.
故选:A.
【点评】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.
对具有线性相关关系的变量x,y,测得一组数据如下表:
x
2
4
5
6
8
y
20
40
60
70
80
根据上表,利用最小二乘法得它们的回归直线方程为 =10.5x+
=10.5x+ ,据此模型来预测当x=20时,y的估计值为( )
,据此模型来预测当x=20时,y的估计值为( )
A.210 B.210.5 C.211.5 D.212.5
知识点:4.回归分析的基本思想及其初步应用
C
【考点】线性回归方程.
【专题】概率与统计.
【分析】求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程求出a,最后将x=20代入求出相应的y即可.
【解答】解:∵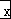 =
=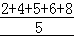 =5,
=5,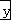 =
=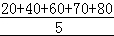 =54
=54
∴这组数据的样本中心点是(5,54)
把样本中心点代入回归直线方程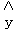 =10.5x+
=10.5x+ ,∴54=10.5×5+a,
,∴54=10.5×5+a,
∴a=1.5,
∴回归直线方程为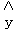 =10.5x+1.5,当x=20时,
=10.5x+1.5,当x=20时,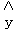 =10.5×20+1.5=211.5,
=10.5×20+1.5=211.5,
故选C.
【点评】本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.
已知函数f(x)= sin2x+cos2x﹣m在[0,
sin2x+cos2x﹣m在[0, ]上有两个零点,则实数m的取值范围是( )
]上有两个零点,则实数m的取值范围是( )
A.(﹣1,2) B.[1,2) C.(﹣1,2] D.[1,2]
知识点:4.和角公式与倍(半)角公式
B
【考点】两角和与差的正弦函数;函数的零点.
【专题】三角函数的图像与性质.
【分析】由题意可知g(x)=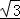 sin2x+cos2x与直线y=m在[0,
sin2x+cos2x与直线y=m在[0,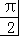 ]上两个交点,数形结合可得m的取值范围.
]上两个交点,数形结合可得m的取值范围.
【解答】解:由题意可得函数g(x)=2sin(2x+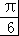 ) 与直线y=m在[0,
) 与直线y=m在[0,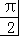 ]上两个交点.
]上两个交点.
由于x∈[0,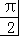 ],故2x+
],故2x+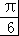 ∈[
∈[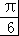 ,
,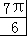 ],故g(x)∈[﹣1,2].
],故g(x)∈[﹣1,2].
令2x+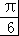 =t,则t∈[
=t,则t∈[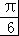 ,
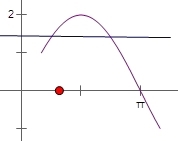
,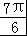 ],函数y=h(t)=2sint 与直线y=m在[
],函数y=h(t)=2sint 与直线y=m在[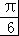 ,
,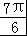 ]上有两个交点,
]上有两个交点,
如图:
要使的两个函数图形有两个交点必须使得1≤m<2,
故选B.
【点评】本题主要考查方程根的存在性及个数判断,两角和差的正弦公式,体现了转化与数形结合的数学思想,属于中档题.
已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+ >0,若a=
>0,若a= f(
f( ),b=﹣2f(﹣2),c=(ln
),b=﹣2f(﹣2),c=(ln )f(ln
)f(ln ),则a,b,c的大小关系正确的是( )
),则a,b,c的大小关系正确的是( )
A.a<b<c B.b<c<a C.a<c<b D.c<a<b
知识点:3.导数在研究函数中的应用
C
【考点】利用导数研究函数的单调性.
【专题】导数的概念及应用.
【分析】利用条件构造函数h(x)=xf(x),然后利用导数研究函数h(x)的单调性,利用函数的单调性比较大小.
【解答】解:设h(x)=xf(x),
∴h′(x)=f(x)+x•f′(x),
∵y=f(x)是定义在实数集R上的奇函数,
∴h(x)是定义在实数集R上的偶函数,
当x>0时,h'(x)=f(x)+x•f′(x)>0,
∴此时函数h(x)单调递增.
∵a=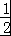 f(
f(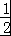 )=h(
)=h(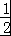 ),b=﹣2f(﹣2)=2f(2)=h(2),
),b=﹣2f(﹣2)=2f(2)=h(2),
c=(ln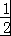 )f(ln
)f(ln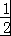 )=h(ln
)=h(ln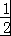 )=h(﹣ln2)=h(ln2),
)=h(﹣ln2)=h(ln2),
又2>ln2>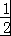 ,
,
∴b>c>a.
故选:C.
【点评】本题考查如何构造新的函数,利用单调性比较大小,是常见的题目.本题属于中档题.
若在区域 内任取一点P,则点P落在单位圆x2+y2=1内的概率为 .
内任取一点P,则点P落在单位圆x2+y2=1内的概率为 .
知识点:3.二元一次不等式(组)与简单的线性规划
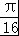
【考点】几何概型.
【专题】计算题.
【分析】由 我们易画出图象求出其对应的面积,即所有基本事件总数对应的几何量,再求出区域内也单位圆重合部分的面积,代入几何概型计算公式,即可得到答案.
我们易画出图象求出其对应的面积,即所有基本事件总数对应的几何量,再求出区域内也单位圆重合部分的面积,代入几何概型计算公式,即可得到答案.
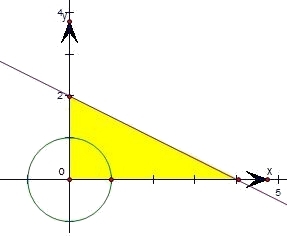
【解答】解:满足约束条件  区域为△ABC内部(含边界),
区域为△ABC内部(含边界),
与单位圆x2+y2=1的公共部分如图中阴影部分所示,
则点P落在单位圆x2+y2=1内的概率概率为
P=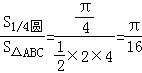 .
.
故答案为: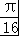 .
.
【点评】本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=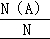 求解.
求解.
已知向量 ,
, 满足|
满足| |=1,|
|=1,| |=3
|=3 ,|2
,|2 ﹣
﹣ |=
|= ,则
,则 与
与 的夹角为 .
的夹角为 .
知识点:4.平面向量的数量积(夹角、模)

【考点】数量积表示两个向量的夹角.
【专题】平面向量及应用.
【分析】设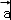 与
与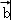 的夹角为θ,则由题意可得 4
的夹角为θ,则由题意可得 4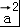 ﹣4
﹣4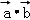 +
+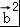 =10,求得cosθ 的值,再结合θ∈[0,π),可得θ的值.
=10,求得cosθ 的值,再结合θ∈[0,π),可得θ的值.
【解答】解:设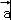 与
与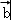 的夹角为θ,则由题意可得 4
的夹角为θ,则由题意可得 4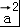 ﹣4
﹣4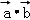 +
+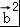 =10,
=10,
即 4﹣4×1×3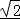 ×cosθ+18=10,求得cosθ=
×cosθ+18=10,求得cosθ=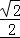 ,
,
再结合θ∈[0,π),可得θ=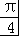 ,
,
故答案为: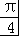 .
.
【点评】本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于基础题.
已知函数f(x)= ,则f(6)= .
,则f(6)= .
知识点:12.绝对值函数与分段函数及其他函数
1
【考点】抽象函数及其应用.
【专题】函数的性质及应用.
【分析】直接利用分段函数以及抽象函数求解即可.
【解答】解:函数f(x)=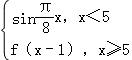 ,
,
则f(6)=f(5)=f(4)=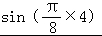 =1.
=1.
故答案为:1.
【点评】本题考查函数的值的求法,抽象函数的应用,考查计算能力.
已知a>0,b>0,且a+2b=1,则 的最小值为 .
的最小值为 .
知识点:4.基本不等式
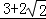
【考点】基本不等式.
【专题】不等式的解法及应用.
【分析】利用“乘1法”和基本不等式的性质即可得出.
【解答】解:∵a>0,b>0,且a+2b=1,
∴ =(a+2b)
=(a+2b)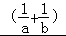 =3+
=3+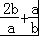
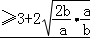 =
=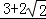 ,当且仅当a=
,当且仅当a=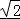 b时取等号.
b时取等号.
∴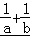 的最小值为
的最小值为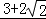 .
.
故答案为: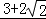 .
.
【点评】本题考查了“乘1法”和基本不等式的性质,属于基础题.
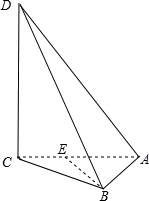
某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为 .

知识点:2.空间几何体的三视图和直观图
2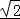
【考点】由三视图求面积、体积.
【专题】立体几何.
【分析】由主视图知CD⊥平面ABC、B点在AC上的射影为AC中点及AC长,由左视图可知CD长及△ABC中变AC的高,利用勾股定理即可求出最长棱BD的长.
【解答】解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;
由主视图知CD=2,由左视图知BE=1,
在Rt△BCE中,BC=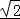 ,
,
在Rt△BCD中,BD= ,
,
在Rt△ACD中,AD=2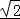 .
.
则三棱锥中最长棱的长为2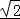 .
.
故答案为:2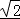 .
.
【点评】本题考查点、线、面间的距离计算,考查空间图形的三视图,考查学生的空间想象能力,考查学生分析解决问题的能力.
已知向量 =(
=( sinx,
sinx, cosx),
cosx), =(cosx,cosx),函数f(x)=
=(cosx,cosx),函数f(x)= •
• .
.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,若f(A)= ,a=
,a= ,S△ABC=
,S△ABC= ,求b+c的值.
,求b+c的值.
知识点:4.平面向量的数量积(夹角、模)
【考点】余弦定理;平面向量数量积的运算;两角和与差的正弦函数.
【专题】解三角形.
【分析】(1)由两向量的坐标,以及平面向量的数量积运算法则列出f(x)解析式,利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,利用正弦函数的单调性确定出f(x)的递增区间即可;
(2)由f(A)=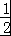 ,求出A的度数,利用三角形面积公式列出关系式,把sinA与已知面积代入求出bc的值,再利用余弦定理列出关系式,把a,cosA的值代入,利用完全平方公式变形,把bc的值代入计算求出b+c的值即可.
,求出A的度数,利用三角形面积公式列出关系式,把sinA与已知面积代入求出bc的值,再利用余弦定理列出关系式,把a,cosA的值代入,利用完全平方公式变形,把bc的值代入计算求出b+c的值即可.
【解答】解:(1)∵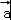 =(
=(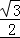 sinx,
sinx,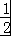 cosx),
cosx),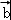 =(cosx,cosx),
=(cosx,cosx),
∴f(x)=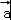 •
•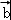 =
=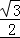 sinxcosx+
sinxcosx+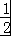 cos2x=
cos2x=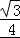 sin2x+
sin2x+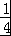 cos2x+
cos2x+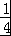 =
=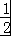 sin(2x+
sin(2x+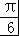 )+
)+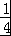 ,
,
令﹣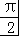 +2kπ≤2x+
+2kπ≤2x+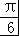 ≤
≤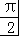 +2kπ,k∈Z,得到﹣
+2kπ,k∈Z,得到﹣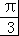 +kπ≤x≤
+kπ≤x≤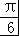 +kπ,k∈Z,
+kπ,k∈Z,
则f(x)的单调递增区间为[﹣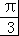 +kπ,
+kπ,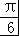 +kπ],k∈Z;
+kπ],k∈Z;
(2)由f(A)=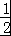 ,得到
,得到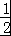 sin(2A+
sin(2A+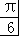 )+
)+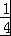 =
= ,即sin(2A+
,即sin(2A+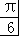 )=
)= ,
,
∴2A+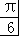 =
=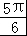 ,即A=
,即A=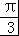 ,
,
∵a=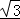 ,S△ABC=
,S△ABC=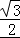 ,
,
∴由三角形面积公式得: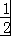 bcsinA=
bcsinA=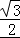 ,即bc=2,
,即bc=2,
由余弦定理得:a2=b2+c2﹣2bccosA,即3=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣6,
即(b+c)2=9,
解得:b+c=3.
【点评】此题考查了余弦定理,平面向量的数量积运算,熟练掌握余弦定理是解本题的关键.
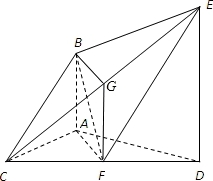
如图,已知AB⊥平面ACD,DE∥AB,AC=AD=DE=2AB,且F是CD的中点.
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.

知识点:5.直线、平面平行的判定及其性质
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【专题】证明题;空间位置关系与距离.
【分析】(Ⅰ)取EC中点G,连BG,GF,证明四边形ABGF为平行四边形,可得AF∥BG,利用线面平行的判定定理,即可得出结论;
(Ⅱ)证明BG⊥DE,BG⊥CD,可得BG⊥平面CDE,利用面面垂直的判定定理,即可得出结论
【解答】证明:(Ⅰ)取EC中点G,连BG,GF.
∵F是CD的中点,∴FG∥DE,且FG=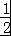 DE.
DE.
又∵AB∥DE,且AB=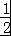 DE.
DE.
∴四边形ABGF为平行四边形.
∴AF∥BG.
又BG⊂平面BCE,AF⊄平面BCE.
∴AF∥平面BCE.
(Ⅱ)∵AB⊥平面ACD,AF⊂平面ACD,
∴AB⊥AF.
∵AB∥DE,∴AF⊥DE.
又∵△ACD为正三角形,∴AF⊥CD.
∵BG∥AF,∴BG⊥DE,BG⊥CD.
∵CD∩DE=D,∴BG⊥平面CDE.
∵BG⊂平面BCE,∴平面BCE⊥平面CDE.
【点评】本题考查线面平行,面面垂直,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(Ⅰ)求参加笔试的竞聘者能被聘用的概率;
(Ⅱ)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(Ⅲ)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
知识点:2.古典概型
【考点】列举法计算基本事件数及事件发生的概率.
【专题】概率与统计.
【分析】(Ⅰ)设参加笔试的竞聘者能被聘用的概率P,依题意有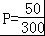 ,计算求得结果.
,计算求得结果.
(Ⅱ)设被聘用的女职工的人数为x,用50乘以女职工所占的比例,即得所求.
(Ⅲ)用列举法求得所有的选法共有10种,其中至少选一名女同志有共有7种,由此求得至少选派一名女同志参加的概率.
【解答】解:(Ⅰ)设参加笔试的竞聘者能被聘用的概率P,依题意有: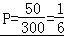 .
.
(Ⅱ)设被聘用的女职工的人数为x,则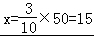 ,
,
即被聘用的女职工的人数为15人.
(Ⅲ)设聘用的三男同志为a,b,c,两个女同志记为m,n,
选派两人的基本事件有:(a,b),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),(c,n),(m,n),共10种,
至少选一名女同志有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(m,n)
共有7种,
∵每种情况出现的可能性相等,所以至少选派一名女同志参加的概率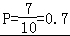 .
.
【点评】本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题.
已知函数f(x)= ax2﹣2lnx,a∈R.
ax2﹣2lnx,a∈R.
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.
【专题】综合题;导数的概念及应用.
【分析】(Ⅰ)求导函数,可得切线的斜率,求出切点坐标,利用点斜式可得切线方程;
(Ⅱ)先求出函数的导数,通过讨论a的取值范围求出函数的单调区间.
【解答】解:(Ⅰ)当a=1时,f(x)=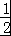 x2﹣2lnx+x,f(1)=
x2﹣2lnx+x,f(1)=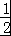 ,
,
∵f′(x)=x﹣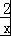 ,
,
∴切线的斜率k=f′(1)=﹣1,
∴切线方程为:y﹣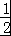 =﹣(x﹣1),
=﹣(x﹣1),
即2x+2y﹣3=0;
(Ⅱ)由题意知:f(x)的定义域为(0,+∞),f′(x)=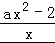 (x>0),
(x>0),
a≤0时,f′(x)<0,f(x)的单调递减区间为:(0,+∞),
a>0时,f(x)在(0,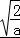 )递减,在(
)递减,在(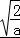 ,+∞)递增.
,+∞)递增.
【点评】本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,正确求导,合理分类是关键.
(13分)已知数列{an}的前n项和为Sn,且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ,求数列{cn}的前2n项和T2n.
,求数列{cn}的前2n项和T2n.
知识点:6.数列的求和
【考点】数列递推式;数列的求和.
【专题】计算题.
【分析】(1)当n=1,可求a1,n≥2时,an=Sn﹣Sn﹣1可得an与an﹣1的递推关系,结合等比数列的通项公式可求an,由bn+1=bn+2,可得{bn}是等差数列,结合等差数列的通项公式可求bn.
(2)由题意可得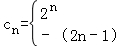
 ,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
【解答】解:(1)当n=1,a1=2; …
当n≥2时,an=Sn﹣Sn﹣1=2an﹣2an﹣1,
∴an=2an﹣1.…
∴{an}是等比数列,公比为2,首项a1=2,
∴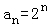 .…
.…
由bn+1=bn+2,得{bn}是等差数列,公差为2.…
又首项b1=1,
∴bn=2n﹣1.…
(2)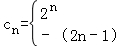
 …
…
∴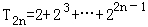 +[3+7+…+(4n﹣1)]
+[3+7+…+(4n﹣1)]
=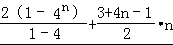
=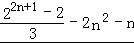 . …
. …
【点评】本题主要考查了等差数列、等比数列的通项公式的应用及求和公式的应用,体现了分类讨论思想的应用
(14分)设函数f(x)=aex(x+1)(其中e=2.71828…),g(x)=x2+bx+2,已知它们在x=0处有相同的切线.
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求函数f(x)在[t,t+1](t>﹣3)上的最小值;
(Ⅲ)判断函数F(x)=2f(x)﹣g(x)+2零点个数.
知识点:3.导数在研究函数中的应用
【考点】导数在最大值、最小值问题中的应用.
【专题】综合题;导数的综合应用.
【分析】(Ⅰ)求导函数,利用两函数在x=0处有相同的切线,可得2a=b,f(0)=a=g(0)=2,即可求函数f(x),g(x)的解析式;
(Ⅱ)求导函数,确定函数的单调性,再分类讨论,即可求出函数f(x)在[t,t+1](t>﹣3)上的最小值;
(Ⅲ)F(x)=4ex(x+1)﹣x2﹣4x,求导,确定F(x)在(﹣∞,﹣2),(﹣ln2,+∞)上单调递增,在(﹣2,﹣ln2)上单调递减,即可得出结论.
【解答】解:(Ⅰ) f'(x)=aex(x+2),g'(x)=2x+b﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
由题意,两函数在x=0处有相同的切线.
∴f'(0)=2a,g'(0)=b,
∴2a=b,f(0)=a=g(0)=2,
∴a=2,b=4,
∴f(x)=2ex(x+1),g(x)=x2+4x+2.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(Ⅱ)f'(x)=2ex(x+2),由f'(x)>0得x>﹣2,由f'(x)<0得x<﹣2,
∴f(x)在(﹣2,+∞)单调递增,在(﹣∞,﹣2)单调递减.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∵t>﹣3,∴t+1>﹣2
①当﹣3<t<﹣2时,f(x)在[t,﹣2]单调递减,[﹣2,t+1]单调递增,
∴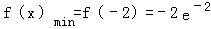 .﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
②当t≥﹣2时,f(x)在[t,t+1]单调递增,∴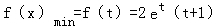 ;
;
∴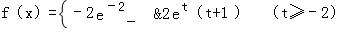 ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(Ⅲ)由题意F(x)=4ex(x+1)﹣x2﹣4x
求导得F'(x)=4ex(x+1)+4ex﹣2x﹣4=2(x+2)(2ex﹣1),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
由F'(x)>0得x>﹣ln2或x<﹣2,由F'(x)<0得﹣2<x<﹣ln2
∴F(x)在(﹣∞,﹣2),(﹣ln2,+∞)上单调递增,在(﹣2,﹣ln2)上单调递减﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∴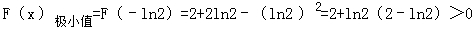 ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∵F(﹣4)=4e﹣4×(﹣4+1)﹣16+16=﹣12e﹣4<0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
故函数F(x)=2f(x)﹣g(x)+2只有一个零点.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)
【点评】本题考查导数的几何意义,考查函数的单调性,考查函数的零点,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.