已知集合A={x|x2﹣x﹣2≤0},集合B={x|1<x≤3},则A∪B= .
知识点:3.集合的基本运算
{x|﹣1≤x≤3}
【考点】1D:并集及其运算.
【分析】求解一元二次不等式化简集合A,然后直接利用并集运算得答案.
【解答】解:由x2﹣x﹣2≤0,解得﹣1≤x≤2.
∴A={x|﹣1≤x≤2},
又集合B={x|1<x≤3},
∴A∪B={x|﹣1≤x≤3},
故答案为:{x|﹣1≤x≤3},
已知a,b∈R,i是虚数单位,若a+i=1﹣bi,则(a+bi)8= .
知识点:3.复数代数形式的四则运算
16
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数相等求得a,b的值,代入(a+bi)8,再由复数代数形式的乘法运算化简得答案.
【解答】解:由a+i=1﹣bi,得a=1,b=﹣1,
从而(a+bi)8=(1﹣i)8=(﹣2i)4=16.
故答案为:16.
从某班抽取5名学生测量身高(单位:cm),得到的数据为160,162,159,160,159,则该组数据的方差s2= .
知识点:2.用样本估计总体
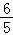
【考点】BC:极差、方差与标准差.
【分析】求出数据的平均数,从而求出方差即可.
【解答】解:数据160,162,159,160,159的平均数是:160,
则该组数据的方差s2=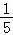 (02+22+12+02+12)=
(02+22+12+02+12)=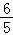 ,
,
故答案为: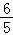 .
.
若双曲线x2+my2=1过点(﹣ ,2),则该双曲线的虚轴长为 .
,2),则该双曲线的虚轴长为 .
知识点:2.双曲线
4
【考点】KC:双曲线的简单性质.
【分析】根据条件求出双曲线的标准方程即可得到结论.
【解答】解:∵双曲线x2+my2=1过点(﹣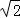 ,2),
,2),
∴2+4m=1,即4m=﹣1,
m=﹣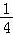 ,
,
则双曲线的标准范围为x2﹣ =1,
=1,
则b=2,
即双曲线的虚轴长2b=4,
故答案为:4.
根据如图所示的伪代码,可知输出的结果S为 .

知识点:2.基本算法语句
205
【考点】E5:顺序结构.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件i=2n+1,n∈N,i=i+2≥100时,S=2i+3的值
【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:
该程序的作用是输出满足条件i=2n+1,n∈N,i=i+2≥100时,
S=2i+3的值,
∵i+2=101时,满足条件,
∴输出的S值为S=2×101+3=205.
故答案为:205.
在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为 .
知识点:2.古典概型
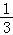
【考点】C5:互斥事件的概率加法公式.
【分析】利用列举法求出甲、乙两人各抽取1张的基本事件的个数和两人都中奖包含的基本事件的个数,由此能求出两人都中奖的概率.
【解答】解:设一、二等奖各用A,B表示,另1张无奖用C表示,
甲、乙两人各抽取1张的基本事件有AB,AC,BA,BC,CA,CB共6个,
其中两人都中奖的有AB,BA共2个,
故所求的概率P=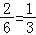 .
.
故答案为: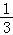 .
.
已知函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<π)的图象如图所示,则该函数的解析式是 .

知识点:7.函数y=Asin(wx+@)+B
y=2sin(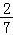 x+
x+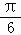 )
)
【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】由图可知,A=2,由点(0,1)在函数的图象上,可得sinφ=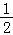 ,利用五点作图法可解得φ,又点(﹣
,利用五点作图法可解得φ,又点(﹣ ,0)在函数的图象上,可得﹣
,0)在函数的图象上,可得﹣ ω+
ω+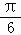 =kπ,k∈Z,进而解得ω,从而得解该函数的解析式.
=kπ,k∈Z,进而解得ω,从而得解该函数的解析式.
【解答】解:∵由图知A=2,y=2sin(ωx+φ),
∵点(0,1),在函数的图象上,
∴2sinφ=1,解得:sinφ=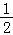 ,
,
∴利用五点作图法可得:φ=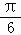 ,
,
∵点(﹣ ,0),在函数的图象上,可得:2sin(﹣
,0),在函数的图象上,可得:2sin(﹣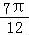 ω+
ω+ )=0,
)=0,
∴可得:﹣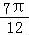 ω+
ω+ =kπ,k∈Z,
=kπ,k∈Z,
解得:ω=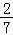 ﹣
﹣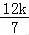 ,k∈Z,
,k∈Z,
∵ω>0,
∴当k=0时,ω=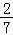 ,
,
∴y=2sin(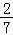 x+
x+ ).
).
故答案为:y=2sin(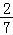 x+
x+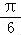 ).
).
如图,在长方体ABCD﹣A1B1C1D1中,对角线B1D与平面A1BC1交于E点.记四棱锥E﹣A1B1C1D1的体积为V1,长方体ABCD﹣A1B1C1D1的体积为V2,则 的值是 .
的值是 .

知识点:3.空间几何体的表面积与体积
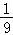
【考点】LF:棱柱、棱锥、棱台的体积.
【分析】连接B1D1∩A1C1=F,证明以E是△A1BC1的重心,那么点E到平面A1B1C1D1的距离是BB1的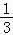 ,利用体积公式,即可得出结论.
,利用体积公式,即可得出结论.
【解答】解:连接B1D1∩A1C1=F,平面A1BC1∩平面BDD1B1=BF,
因为E∈平面A1BC1,E∈平面BDD1B1,所以E∈BF,
连接BD,因为F是A1C1的中点,所以BF是中线,
又根据B1F平行且等于 BD,所以
BD,所以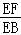 =
= ,
,
所以E是△A1BC1的重心,那么点E到平面A1B1C1D1的距离是BB1的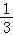 ,
,
所以V1=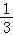
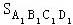 ×
×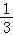 BB1,
BB1,
而V2=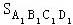 ×BB1,
×BB1,
所以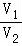 =
=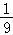 .
.
故答案为: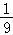 .
.

已知实数x,y满足 ,则
,则 的取值范围是 .
的取值范围是 .
知识点:3.二元一次不等式(组)与简单的线性规划
[1,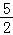 ]
]
【考点】7C:简单线性规划.
【分析】作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
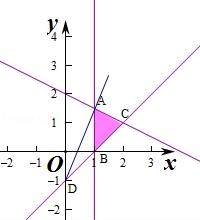
【解答】解:作出不等式组对应的平面区域,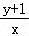 的几何意义是区域内的点到定点D(0,﹣1)的斜率,
的几何意义是区域内的点到定点D(0,﹣1)的斜率,
由图象知,AD的斜率最大,
BD的斜率最小,此时最小值为1,
由 得
得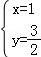 ,即A(1,
,即A(1,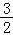 ),
),
此时AD的斜率k=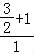 =
= ,
,
即1≤ ≤
≤ ,
,
故 的取值范围是[1,
的取值范围是[1, ]
]
故答案为:[1, ]
]
已知{an},{bn}均为等比数列,其前n项和分别为Sn,Tn,若对任意的n∈N*,总有 =
= ,则
,则 = .
= .
知识点:5.等比数列的前n项和
9
【考点】8E:数列的求和.
【分析】设{an},{bn}的公比分别为q,q′,利用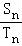 =
=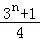 ,求出q=9,q′=3,可得
,求出q=9,q′=3,可得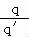 =3,即可求得结论.
=3,即可求得结论.
【解答】解:设{an},{bn}的公比分别为q,q′,
∵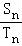 =
=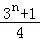 ,
,
∴n=1时,a1=b1.
n=2时,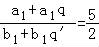 .
.
n=3时, .
.
∴2q﹣5q′=3,7q′2+7q′﹣q2﹣q+6=0,
解得:q=9,q′=3,
∴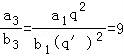 .
.
故答案为:9.
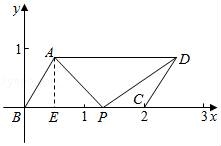
已知平行四边形ABCD中.∠BAD=120°,AB=1,AD=2,点P是线段BC上的一个动点,则 •
• 的取值范围是 .
的取值范围是 .
知识点:4.平面向量的数量积(夹角、模)
[﹣ ,2]
,2]
【考点】9R:平面向量数量积的运算.
【分析】以为坐标原点,以BC所在的直线为x轴,建立如图所述的直角坐标系,作AE⊥BC,垂足为E,求出A(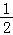 ,
,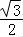 ),D(
),D(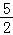 ,
,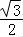 ),设点P(x,0),0≤x≤2,
),设点P(x,0),0≤x≤2,
根据向量的坐标运算以及向量的数量积的运算得到 •
•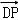 =(x﹣
=(x﹣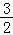 )2﹣
)2﹣ ,根据二次函数的性质即可求出答案.
,根据二次函数的性质即可求出答案.
【解答】解:以B为坐标原点,以BC所在的直线为x轴,建立如图所述的直角坐标系,作AE⊥BC,
垂足为E,
∵∠BAD=120°,AB=1,AD=2,
∴∠ABC=60°,
∴AE=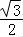 ,BE=
,BE=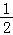 ,
,
∴A(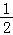 ,
,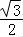 ),D(
),D(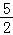 ,
,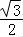 ),
),
∵点P是线段BC上的一个动点,设点P(x,0),0≤x≤2,
∴ =(x﹣
=(x﹣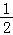 ,﹣
,﹣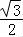 ),
),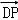 =(x﹣
=(x﹣ ,﹣
,﹣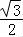 ),
),
∴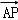 •
•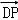 =(x﹣
=(x﹣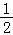 )(x﹣
)(x﹣ )+
)+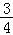 =(x﹣
=(x﹣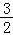 )2﹣
)2﹣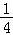 ,
,
∴当x=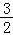 时,有最小值,最小值为﹣
时,有最小值,最小值为﹣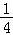 ,
,
当x=0时,有最大值,最大值为2,
则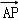 •
• 的取值范围为[﹣
的取值范围为[﹣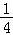 ,2],
,2],
故答案为:[﹣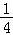 ,2].
,2].
如图,已知椭圆 +
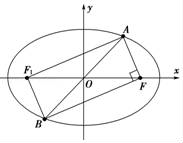
+ =1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF=
=1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF= 时,椭圆的离心率为 .
时,椭圆的离心率为 .

知识点:1.椭圆
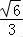
【考点】K4:椭圆的简单性质.
【分析】设椭圆的左焦点为F1,连结AF1,BF1,通过|AB|=|F1F|=2c,所以在Rt△ABF中,|AF|=2csin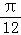 ,
,
|BF|=2ccos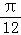 ,由椭圆定义,转化求解离心率即可.
,由椭圆定义,转化求解离心率即可.
【解答】解:设椭圆的左焦点为F1,连结AF1,BF1,由对称性及AF⊥BF可知,四边形AFBF1是矩形,所以|AB|=|F1F|=2c,所以在Rt△ABF中,|AF|=2csin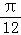 ,
,
|BF|=2ccos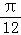 ,由椭圆定义得:
,由椭圆定义得:
2c(cos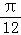 +sin
+sin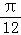 )=2a,即:
)=2a,即:
e= =
= =
=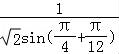 =
=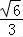 .
.
故答案为: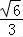 .
.
在斜三角形ABC中,a,b,c分别是角A,B,C所对的边,若 +
+ =
= ,则
,则 的最大值为 .
的最大值为 .
知识点:9.正弦定理和余弦定理(解三角形)
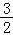
【考点】HR:余弦定理;HP:正弦定理.
【分析】由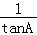 +
+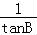 =
=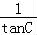 可得,
可得,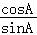 +
+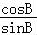 =
= ,通分化简,根据正弦定理及余弦定理在化简,利用基本不等式的性质求解.
,通分化简,根据正弦定理及余弦定理在化简,利用基本不等式的性质求解.
【解答】解:由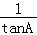 +
+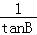 =
= 可得,
可得, +
+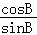 =
=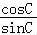 ,
,
即 =
=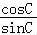 ,
,
∴ =
=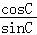 ,即
,即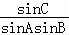 =
=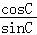 ,
,
∴sin2C=sinAsinBcosC.
根据正弦定理及余弦定理可得,c2=ab•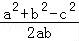 ,整理得a2+b2=3c2,
,整理得a2+b2=3c2,
∴ =
= ≤
≤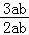 =
=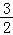 ,当且仅当a=b时等号成立.
,当且仅当a=b时等号成立.
故答案为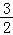 .
.
对于实数a,b,定义运算“□”:a□b= 设f(x)=(x﹣4)□(
设f(x)=(x﹣4)□( x﹣4),若关于x的方程|f(x)﹣m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是 .
x﹣4),若关于x的方程|f(x)﹣m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是 .
知识点:13.函数与方程
(﹣1,1)∪(2,4)
【考点】54:根的存在性及根的个数判断.
【分析】根据新定义得出f(x)的解析式,作出f(x)的函数图象,则f(x)与y=m±1共有4个交点,根据图象列出不等式组解出.
【解答】解:解不等式x﹣4≤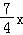 ﹣4得x≥0,f(x)=
﹣4得x≥0,f(x)= ,
,
画出函数f(x)的大致图象如图所示.
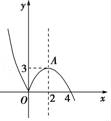
因为关于x的方程|f(x)﹣m|=1(m∈R),即f(x)=m±1(m∈R)恰有四个互不相等的实数根,
所以两直线y=m±1(m∈R)与曲线y=f(x)共有四个不同的交点,
∴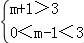 或
或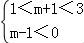 或
或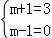 ,
,
解得2<m<4或﹣1<m<1.
故答案为(﹣1,1)∪(2,4).
设α为锐角,且cos(α+ )=
)= .
.
(1)求cos( )的值;
)的值;
(2)求cos(2α﹣ )的值.
)的值.
知识点:5.三角函数的求值、化简与证明
【考点】GP:两角和与差的余弦函数.
【分析】(1)由已知及同角三角函数基本关系式可求sin(α+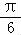 ),利用诱导公式即可得解cos(
),利用诱导公式即可得解cos(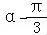 )的值.
)的值.
(2)利用诱导公式可求sin(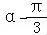 ),由2α
),由2α =(α+
=(α+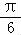 )﹣(
)﹣(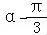 ),利用两角差的余弦函数公式即可计算得解.
),利用两角差的余弦函数公式即可计算得解.
【解答】(本题满分为14分)
解:(1)∵α为锐角,
∴α+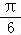 ∈(
∈(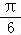 ,
, ).
).
又cos(α+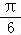 )=
)=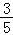 ,故sin(α+
,故sin(α+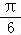 )=
)=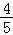 ,…4分
,…4分
∴cos(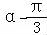 )=cos[
)=cos[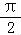 ﹣(α+
﹣(α+ )]=sin(α+
)]=sin(α+ )=
)=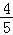 ,…6分
,…6分
(2)又sin(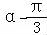 )=﹣sin[
)=﹣sin[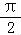 ﹣(α+
﹣(α+ )]=﹣cos(α+
)]=﹣cos(α+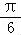 )=﹣
)=﹣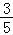 ,…8分
,…8分
故cos(2α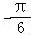 )=cos[(α+
)=cos[(α+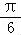 )﹣(
)﹣(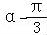 )]
)]
=cos(α+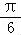 )cos(
)cos(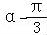 )﹣sin(α+
)﹣sin(α+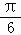 )sin(
)sin( )
)
=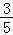 ×
× ﹣
﹣ ×(﹣
×(﹣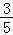 )
)
= …14分
…14分
在直三棱柱ABC﹣A1B1C1中,CA=CB,AA1= AB,D是AB的中点
AB,D是AB的中点
(1)求证:BC1∥平面A1CD;
(2)若点P在线段BB1上,且BP= BB1,求证:AP⊥平面A1CD.
BB1,求证:AP⊥平面A1CD.

知识点:5.直线、平面平行的判定及其性质
【考点】LW:直线与平面垂直的判定;LS:直线与平面平行的判定.
【分析】(1)连接AC1,设与CA1 交于O点,连接OD,由O为AC1 的中点,D是AB的中点,可得OD∥BC1,即可证明BC1∥平面A1CD.
(2)法一:设AB=x,则证明△ABP∽△ADA1,可得AP⊥A1D,又由线面垂直的性质可得CD⊥AP,从而可证AP⊥平面A1CD;
法二:由题意,取A1B1 的中点O,连接OC1,OD,分别以OC1,OA1,OD为x,y,z轴建立空间直角坐标系,设OA1=a,OC1=b,由题意可得各点坐标,可求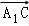 =(b,﹣a,2
=(b,﹣a,2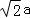 ),
),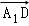 =(0.﹣a,2
=(0.﹣a,2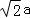 ),
),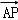 =(0,﹣2a,﹣
=(0,﹣2a,﹣ ),由
),由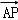 •
•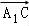 =0,
=0,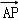 •
•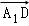 =0,即可证明AP⊥平面A1CD.
=0,即可证明AP⊥平面A1CD.
【解答】证明:(1)如图,连接AC1,设与CA1 交于O点,连接OD
∴直三棱柱ABC﹣A1B1C1中,O为AC1 的中点,
∵D是AB的中点,
∴△ABC1中,OD∥BC1,
又∵OD⊂平面A1CD,
∴BC1∥平面A1CD.
(2)法一:由题意,设AB=x,则BP= x,AD=
x,AD=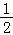 x,A1A=
x,A1A=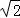 x,
x,
由于 =
=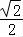 ,
,
∴△ABP∽△ADA1,可得∠BAP=∠AA1D,
∵∠DA1A+∠ADA1=90°,可得:AP⊥A1D,
又∵CD⊥AB,CD⊥BB1,可得CD⊥平面ABA1B1,
∴CD⊥AP,
∴AP⊥平面A1CD.
法二:由题意,取A1B1 的中点O,连接OC1,OD,分别以OC1,
OA1,OD为x,y,z轴建立空间直角坐标系,设OA1=a,OC1=b,
则:由题意可得各点坐标为:A1(0,a,0),C(b,0,2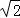 a),
a),
D(0,0,2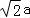 ),P(0,﹣a,
),P(0,﹣a,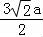 ),A(0,a,2
),A(0,a,2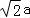 ),
),
可得: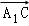 =(b,﹣a,2
=(b,﹣a,2 ),
),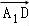 =(0.﹣a,2
=(0.﹣a,2 ),
),
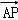 =(0,﹣2a,﹣
=(0,﹣2a,﹣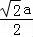 ),
),
所以:由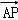 •
•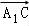 =0,可得:AP⊥A1C,由
=0,可得:AP⊥A1C,由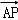 •
•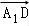 =0,
=0,
可得:AP⊥A1D,
又:A1 C∩A1 D=A1,
所以:AP⊥平面A1CD


如图,直线l是湖岸线,O是l上一点,弧 是以O为圆心的半圆形栈桥,C为湖岸线l上一观景亭,现规划在湖中建一小岛D,同时沿线段CD和DP(点P在半圆形栈桥上且不与点A,B重合)建栈桥,考虑到美观需要,设计方案为DP=DC,∠CDP=60°且圆弧栈桥BP在∠CDP的内部,已知BC=2OB=2(km),设湖岸BC与直线栈桥CD,DP是圆弧栈桥BP围成的区域(图中阴影部分)的面积为S(km2),∠BOP=θ
是以O为圆心的半圆形栈桥,C为湖岸线l上一观景亭,现规划在湖中建一小岛D,同时沿线段CD和DP(点P在半圆形栈桥上且不与点A,B重合)建栈桥,考虑到美观需要,设计方案为DP=DC,∠CDP=60°且圆弧栈桥BP在∠CDP的内部,已知BC=2OB=2(km),设湖岸BC与直线栈桥CD,DP是圆弧栈桥BP围成的区域(图中阴影部分)的面积为S(km2),∠BOP=θ
(1)求S关于θ的函数关系式;
(2)试判断S是否存在最大值,若存在,求出对应的cosθ的值,若不存在,说明理由.

知识点:4.直线与圆的位置关系
【考点】HN:在实际问题中建立三角函数模型.
【分析】(1)根据余弦定理和和三角形的面积公式,即可表示函数关系式,
(2)存在,存在,S′=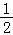 (3cosθ+3
(3cosθ+3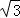 sinθ﹣1),根据两角和差的余弦公式即可求出.
sinθ﹣1),根据两角和差的余弦公式即可求出.
【解答】解:(1)在△COP中,
CP2=CO2+OP2﹣2OC•OPcosθ=10﹣6cosθ,
从而△CDP得面积S△CDP= CP2=
CP2=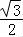 (5﹣3cosθ),
(5﹣3cosθ),
又因为△COP得面积S△COP=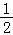 OC•OP=
OC•OP=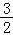 sinθ,
sinθ,
所以S=S△CDP+S△COP﹣S扇形OBP=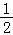 (3sinθ﹣3
(3sinθ﹣3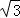 cosθ﹣θ)+
cosθ﹣θ)+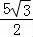 ,0<θ<θ0<π,cosθ0=
,0<θ<θ0<π,cosθ0=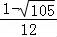 ,
,
当DP所在的直线与半圆相切时,设θ取的最大值为θ0,此时在△COP中,OP=1,
OC=3,∠CPO=30°,CP=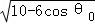 =6sinθ0,cosθ0=
=6sinθ0,cosθ0=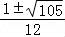 ,
,
(2)存在,S′=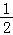 (3cosθ+3
(3cosθ+3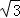 sinθ﹣1),
sinθ﹣1),
令S′=0,得sin(θ+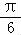 )=
)= ,
,
当0<θ<θ0<π,S′>0,所以当θ=θ0时,S取得最大值,
此时cos(θ0+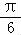 )=﹣
)=﹣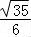 ,
,
∴cosθ0=cos[(θ0+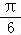 )﹣
)﹣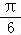 ]=cos(θ0+
]=cos(θ0+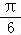 )cos
)cos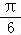 +sin(θ0+
+sin(θ0+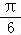 )sin
)sin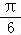 =
=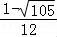
在平面直角坐标系xOy中,设椭圆 (a>b>0)的离心率是e,定义直线y=
(a>b>0)的离心率是e,定义直线y= 为椭圆的“类准线”,已知椭圆C的“类准线”方程为y=
为椭圆的“类准线”,已知椭圆C的“类准线”方程为y= ,长轴长为4.
,长轴长为4.
(1)求椭圆C的方程;
(2)点P在椭圆C的“类准线”上(但不在y轴上),过点P作圆O:x2+y2=3的切线l,过点O且垂直于OP的直线l交于点A,问点A是否在椭圆C上?证明你的结论.
知识点:1.椭圆
【考点】K4:椭圆的简单性质.
【分析】(1)由题意列关于a,b,c的方程,联立方程组求得a2=4,b2=3,c2=1,则椭圆方程可求;
(2)设P(x0,2 )(x0≠0),当x0=
)(x0≠0),当x0= 时和x0=﹣
时和x0=﹣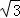 时,求出A的坐标,代入椭圆方程验证知,A在椭圆上,当x0≠±
时,求出A的坐标,代入椭圆方程验证知,A在椭圆上,当x0≠±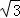 时,求出过点O且垂直于0P的直线与椭圆的交点,写出该交点与P点的连线所在直线方程,由原点到直线的距离等于圆的半径说明直线是圆的切线,从而说明点A在椭圆C上.
时,求出过点O且垂直于0P的直线与椭圆的交点,写出该交点与P点的连线所在直线方程,由原点到直线的距离等于圆的半径说明直线是圆的切线,从而说明点A在椭圆C上.
【解答】解:(1)由题意得: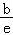 =
= =2
=2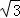 ,2a=4,
,2a=4,
又a2=b2+c2,联立以上可得:
a2=4,b2=3,c2=1.
∴椭圆C的方程为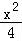 +
+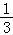 y2=1;
y2=1;
(2)如图,由(1)可知,
椭圆的类准线方程为y=±2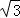 ,
,
不妨取y=2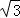 ,
,
设P(x0,2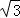 )(x0≠0),
)(x0≠0),
则kOP= ,
,
∴过原点且与OP垂直的直线方程为y=﹣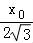 x,
x,
当x0=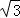 时,过P点的圆的切线方程为x=
时,过P点的圆的切线方程为x= ,
,
过原点且与OP垂直的直线方程为y=﹣ x,
x,
联立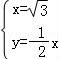 ,解得:A(
,解得:A( ,﹣
,﹣ ),
),
代入椭圆方程成立;
同理可得,当x0=﹣ 时,点A在椭圆上;
时,点A在椭圆上;
当x0≠±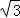 时,
时,
联立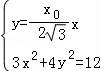 ,
,
解得A1(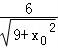 ,﹣
,﹣ ),A2(﹣
),A2(﹣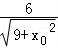 ,
,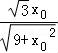 ),
),
PA1所在直线方程为(2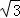
 +
+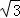 x0)x﹣(x0
x0)x﹣(x0 ﹣6)y﹣
﹣6)y﹣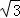 x02﹣12
x02﹣12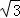 =0.
=0.
此时原点O到该直线的距离d=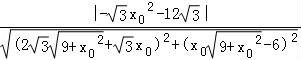 =
= ,
,
∴说明A点在椭圆C上;
同理说明另一种情况的A也在椭圆C上.
综上可得,点A在椭圆C上.

已知数列{an}满足2an+1=an+an+2+k(n∈N*,k∈R),且a1=2,a3+a5=﹣4.
(1)若k=0,求数列{an}的前n项和Sn;
(2)若a4=﹣1,求数列{an}的通项公式an.
知识点:6.数列的求和
【考点】8H:数列递推式;8E:数列的求和.
【分析】(1)若k=0,则数列{an}满足2an+1=an+an+2(n∈N*,k∈R),则数列{an}是等差数列,利用等差数列的前n项和公式即可得出.
(2)2an+1=an+an+2+k(n∈N*,k∈R),a3+a5=﹣4,a4=﹣1,可得2a4=a3+a5+k,k=2.数列{an}满足2an+1=an+an+2+2,利用递推关系可得:2(an+1﹣an)=(an﹣an﹣1)+(an+2﹣an+1),令bn=an+1﹣an,则2bn=bn﹣1+bn+1.数列{bn}是等差数列,即可得出.
【解答】解:(1)若k=0,则数列{an}满足2an+1=an+an+2(n∈N*,k∈R),
∴数列{an}是等差数列,设公差为d,
∵a1=2,a3+a5=﹣4.
∴2×2+6d=﹣4,解得d=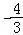 .
.
∴Sn=2n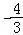 ×
×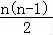 =
= .
.
(2)2an+1=an+an+2+k(n∈N*,k∈R),a3+a5=﹣4,a4=﹣1,
则2a4=a3+a5+k,
﹣2=﹣4+k,
解得k=2.
数列{an}满足2an+1=an+an+2+2,
当n≥2时,2an=an﹣1+an+1+2,
相减可得:2(an+1﹣an)=(an﹣an﹣1)+(an+2﹣an+1),
令bn=an+1﹣an,
则2bn=bn﹣1+bn+1.
∴数列{bn}是等差数列,公差=b4﹣b3=(a5﹣a4)﹣(a4﹣a3)=﹣2.
首项为b1=a2﹣a1,b2=a3﹣a2,b3=a4﹣a3,
由2b2=b1+b3,可得2(a3﹣a2)=a2﹣2﹣1﹣a3,
解得3(a3﹣a2)=﹣3,b2=a3﹣a2=﹣1.
∴bn=b2+(n﹣2)(﹣2)=﹣2n+3.
∴an+1﹣an=﹣2n+3.
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=[﹣2(n﹣1)+3]+[﹣2(n﹣2)+3]+…+(﹣2+3)+2
=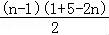 +2
+2
=﹣n2+4n﹣1.
已知函数f(x)=ex( x3﹣2x2+(a+4)x﹣2a﹣4),其中a∈R,e为自然对数的底数.
x3﹣2x2+(a+4)x﹣2a﹣4),其中a∈R,e为自然对数的底数.
(1)关于x的不等式f(x)<﹣ ex在(﹣∞,2)上恒成立,求a的取值范围;
ex在(﹣∞,2)上恒成立,求a的取值范围;
(2)讨论函数f(x)极值点的个数.
知识点:3.导数在研究函数中的应用
【考点】6D:利用导数研究函数的极值;3R:函数恒成立问题.
【分析】(1)原不等式转化为所以a>﹣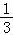 (x﹣2)2,根据函数的单调性即可求出a的范围,
(x﹣2)2,根据函数的单调性即可求出a的范围,
(2)先求导,再构造函数,进行分类讨论,利用导数和函数的极值的关系即可判断.
【解答】解:(1)由f(x)<﹣ ex,得ex(
ex,得ex(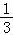 x3﹣2x2+(a+4)x﹣2a﹣4)<﹣
x3﹣2x2+(a+4)x﹣2a﹣4)<﹣ ex,
ex,
即x3﹣6x2+(3a+12)x﹣6a﹣8<0对任意x∈(﹣∞,2)恒成立,
即(6﹣3x)a>x3﹣6x2+12x﹣8对任意x∈(﹣∞,2)恒成立,
因为x<2,所以a>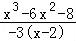 =﹣
=﹣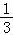 (x﹣2)2,
(x﹣2)2,
记g(x)=﹣ (x﹣2)2,因为g(x)在(﹣∞,2)上单调递增,且g(2)=0,
(x﹣2)2,因为g(x)在(﹣∞,2)上单调递增,且g(2)=0,
所以a≥0,即a的取值范围为[0,+∞);
(2)由题意,可得f′(x)=ex( x3﹣x2+ax﹣a),可知f(x)只有一个极值点或有三个极值点.
x3﹣x2+ax﹣a),可知f(x)只有一个极值点或有三个极值点.
令g(x)= x3﹣x2+ax﹣a,
x3﹣x2+ax﹣a,
①若f(x)有且仅有一个极值点,则函数g(x)的图象必穿过x轴且只穿过一次,即g(x)为单调递增函数或者g(x)极值同号.
(ⅰ)当g(x)为单调递增函数时,g′(x)=x2﹣2x+a≥0在R上恒成立,得a≥1.
(ⅱ)当g(x)极值同号时,设x1,x2为极值点,则g(x1)•g(x2)≥0,
由g′(x)=x2﹣2x+a=0有解,得a<1,且x12﹣2x1+a=0,x22﹣2x2+a=0,
所以x1+x2=2,x1x2=a,
所以g(x1)= x13﹣2x12﹣2+ax1﹣a=
x13﹣2x12﹣2+ax1﹣a= x1(2x1﹣a)﹣
x1(2x1﹣a)﹣ x1+ax1﹣a
x1+ax1﹣a
=﹣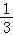 (2x1﹣a)﹣
(2x1﹣a)﹣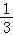 ax1+ax1﹣a=
ax1+ax1﹣a=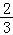 [(a﹣1)x1﹣a],
[(a﹣1)x1﹣a],
同理,g(x2)=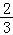 [(a﹣1)x2﹣a],
[(a﹣1)x2﹣a],
所以g(x1)g(x2)=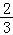 [(a﹣1)x1﹣a]•
[(a﹣1)x1﹣a]•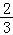 [(a﹣1)x2﹣a]≥0,
[(a﹣1)x2﹣a]≥0,
化简得(a﹣1)2x1x2﹣a(a﹣1)(x1+x2)+a2≥0,
所以(a﹣1)2a﹣2a(a﹣1)+a2≥0,即a≥0,
所以0≤a<1.
所以,当a≥0时,f(x)有且仅有一个极值点;
②若f(x)有三个极值点,则函数g(x)的图象必穿过x轴且穿过三次,同理可得a<0.
综上,当a≥0时,f(x)有且仅有一个极值点,当a<0时,f(x)有三个极值点.