已知集合A={x|x2≥1}, ,则A∩(∁RB)=( )
,则A∩(∁RB)=( )
A.(2,+∞) B.(﹣∞,﹣1]∪(2,+∞) C.(﹣∞,﹣1)∪(2,+∞) D.[﹣1,0]∪[2,+∞)
知识点:3.集合的基本运算
C
【考点】交、并、补集的混合运算.
【专题】集合.
【分析】分别求解一元二次不等式和分式不等式化简集合A,B,然后利用交、并、补集的混合运算得答案.
【解答】解:A={x|x2≥1}={x|x≤﹣1或x≥1},
由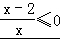 ,得0<x≤2,
,得0<x≤2,
∴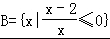 ={x|0<x≤2},
={x|0<x≤2},
∴∁RB={x|x≤0或x>2},
∴A∩(∁RB)=(﹣∞,﹣1)∪(2,+∞).
故选:C.
【点评】本题考查交、并、补集的混合运算,考查了分式不等式的解法,是基础题.
下列函数中,既不是奇函数,也不是偶函数的是( )
A.y=x+sinx B.y=xsinx C.y=x+cosx D.y=xcosx
知识点:5.奇偶性与周期性
C
【考点】余弦函数的奇偶性.
【专题】函数思想;函数的性质及应用.
【分析】直接利用函数奇偶性的定义逐一判断四个选项得答案.
【解答】解:函数y=f(x)=x+sinx的定义域为R,且f(﹣x)=﹣f(x),∴y=x+sinx为奇函数;
y=f(x)=xsinx的定义域为R,且f(﹣x)=f(x),∴y=xsinx为偶函数;
y=x+cosx的定义域为R,由f(﹣x)﹣f(x)=0,得﹣x+cosx﹣x﹣cosx=0,得x=0,不满足对任意x都成立,
由f(﹣x)+f(x)=0,得﹣x+cosx+x+cosx=0,得cosx=0,不满足对任意x都成立,
∴y=x+cosx为非奇非偶函数;
y=f(x)=xcosx的定义域为R,且f(﹣x)=﹣f(x),∴y=xcosx为奇函数.
故选:C.
【点评】本题考查函数就偶性的性质,训练了函数奇偶性的判定方法,是基础题.
下列4个命题:
①命题“若x2﹣x=0,则x=1”的逆否命题为“若x≠1,则x2﹣x≠0”;
②若“¬p或q”是假命题,则“p且¬q”是真命题;
③若p:x(x﹣2)≤0,q:log2x≤1,则p是q的充要条件;
④若命题p:存在x∈R,使得2x<x2,则¬p:任意x∈R,均有2x≥x2;
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
知识点:4.命题及其关系
C
【考点】命题的真假判断与应用.
【专题】简易逻辑.
【分析】直接写出命题的逆否命题判断①;由复合命题的真假判断判定②;求解不等式,然后结合充要条件的判断方法判断③;直接写出特称命题的否定判断④.
【解答】解:①命题“若x2﹣x=0,则x=1”的逆否命题为“若x≠1,则x2﹣x≠0”,①正确;
②若“¬p或q”是假命题,则¬p、q均为假命题,∴p、¬q均为真命题,“p且¬q”是真命题,②正确;
③由p:x(x﹣2)≤0,得0≤x≤2,
由q:log2x≤1,得0<x≤2,则p是q的必要不充分条件,③错误;
④若命题p:存在x∈R,使得2x<x2,则¬p:任意x∈R,均有2x≥x2,④正确.
∴正确的命题有3个.
故选:C.
【点评】本题考查命题的真假判断与应用,考查了命题的否定、逆否命题,训练了充分必要条件的判断方法,是基础题.
已知向量 与向量
与向量 夹角为
夹角为 ,且
,且 ,
, ,则
,则 =( )
=( )
A. B.
B. C.1 D.2
C.1 D.2
知识点:4.平面向量的数量积(夹角、模)
C
【考点】数量积判断两个平面向量的垂直关系.
【专题】计算题;方程思想;平面向量及应用.
【分析】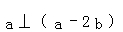 ,可得
,可得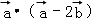 =
= =0,代入解出即可.
=0,代入解出即可.
【解答】解:∵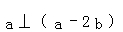 ,
,
∴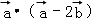 =
= =3﹣2
=3﹣2
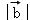 ×
× =0,
=0,
解得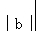 =1.
=1.
故选:C.
【点评】本题查克拉向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.
已知函数f(x)=lnx+x﹣2的零点x0∈[a,b],且b﹣a=1,a,b∈N*,则a+b=( )
A.2 B.3 C.4 D.5
知识点:13.函数与方程
B
【考点】函数零点的判定定理.
【专题】转化思想;数学模型法;函数的性质及应用.
【分析】利用根的存在定理先判断函数零点所在的区间,然后确定与a,b的关系.
【解答】解:因为f(x)=lnx+x﹣2,所以函数在定义域(0,+∞)上单调递增,
因为f(1)=ln1+1﹣2=﹣1<0,f(2)=ln2+2﹣2=ln2>0.
所以在区间[1,2]上,函数存在唯一的一个零点.
在由题意可知,a=1,b=2,所以a+b=3.
故选:B
【点评】本题主要考查函数零点区间的判断以及根的存在性定理的应用,判断函数是单调增函数是解决本题的关键.
已知正项等差数列{an}满足a1+a2015=2,则 的最小值为( )
的最小值为( )
A.1 B.2 C.2014 D.2015
知识点:2.等差数列及其性质
B
【考点】等差数列的性质.
【专题】等差数列与等比数列.
【分析】正项等差数列{an}满足a1+a2015=2,可得a1+a2015=2=a2+a2014,再利用“乘1法”与基本不等式的性质即可得出.
【解答】解:∵正项等差数列{an}满足a1+a2015=2,
∴a1+a2015=2=a2+a2014,
则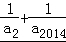 =
=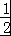 (a2+a2014)
(a2+a2014) =
=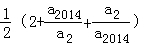 ≥
≥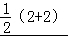 =2,
=2,
当且仅当a2=a2014=1时取等号.
故选:B.
【点评】本题考查了等差数列的性质、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.
设a=lnπ,b=logπe,c=logtan1sin1,则( )
A.c>b>a B.b>c>a C.a>c>b D.a>b>c
知识点:10.对数函数及其性质
D
【考点】对数值大小的比较.
【专题】计算题;函数的性质及应用.
【分析】利用对数函数、三角函数的单调性即可得出.
【解答】解:∵a=lnπ>1,0<b=logπe<1,c=logtan1sin1<0,
∴a>b>c.
故选:D.
【点评】本题考查了对数函数、三角函数的单调性,考查了推理能力与计算能力,属于中档题.
已知函数f(x)=2cosx(sinx+cosx),则下列说法正确的是( )
A.f(x)的最小正周期为2π
B.f(x)的图象关于点 对称
对称
C.f(x)的图象关于直线 对称
对称
D.f(x)的图象向左平移 个单位长度后得到一个偶函数图象
个单位长度后得到一个偶函数图象
知识点:4.和角公式与倍(半)角公式
C
【考点】二倍角的余弦.
【专题】三角函数的图像与性质.
【分析】利用二倍角公式化简可得f(x)=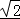 sin(2x+
sin(2x+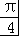 )+1,由正弦函数的图象和性质逐选项判断即可.
)+1,由正弦函数的图象和性质逐选项判断即可.
【解答】解:∵f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+1+cos2x=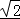 sin(2x+
sin(2x+ )+1,
)+1,
∴f(x)的最小正周期为 ,A错误;
,A错误;
由f(﹣ )=
)=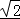 sin0+1=1,B错误;
sin0+1=1,B错误;
由f( )=
)=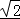 sin
sin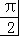 +1=
+1= 1,C正确;
1,C正确;
f(x)的图象向左平移 个单位长度后得到y=
个单位长度后得到y=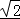 cos(2x+
cos(2x+ )+1,不为偶函数,故D错误.
)+1,不为偶函数,故D错误.
故选:C.
【点评】本题主要考查了二倍角公式,正弦函数的图象和性质的应用,属于基础题.
设函数f(x)=alnx+bx2,若函数f(x)的图象在点(1,1)处的切线与y轴垂直,则实数a+b=( )
A.1 B. C.
C. D.﹣1
D.﹣1
知识点:3.导数在研究函数中的应用
D
【考点】利用导数研究曲线上某点切线方程.
【专题】导数的概念及应用;直线与圆.
【分析】求出函数的导数,求得切线的斜率,由条件可得a+2b=0,b=1,即可求得a+b.
【解答】解:函数f(x)=alnx+bx2的导数为f′(x)= +2bx,
+2bx,
由题意可得,在点(1,1)处的切线斜率为a+2b=0,
又aln1+b=1,解得b=1,a=﹣2,
即a+b=﹣1.
故选:D.
【点评】本题考查导数的运用:求切线的斜率,考查两直线垂直的条件,属于基础题.
已知函数f(x)=ln(1+x2),则满足不等式f(2x﹣1)<f(3)的x的取值范围是( )
A.(﹣∞,2) B.(﹣2,2) C.(﹣1,2) D.(2,+∞)
知识点:3.单调性与最大(小)值
C
【考点】对数函数的单调性与特殊点.
【专题】转化思想;数形结合法;函数的性质及应用.
【分析】可得函数f(x)=ln(1+x2)在(0,+∞)单调递增,在(﹣∞,0)单调递减,原不等式可化为|2x﹣1|<3,解不等式可得.
【解答】解:∵函数f(x)=ln(1+x2),
∴f(﹣x)=ln(1+x2)=f(x),
∴函数f(x)=ln(1+x2)为R上的偶函数,
∵y=lx在(0,+∞)单调递增,
t=1+x2在(0,+∞)单调递增,
∴函数f(x)=ln(1+x2)在(0,+∞)单调递增,在(﹣∞,0)单调递减,
∴不等式f(2x﹣1)<f(3)等价于|2x﹣1|<3,
∴﹣3<2x﹣1<3,解得﹣1<x<2,
故选:C.
【点评】本题考查对数函数的性质,等价转化已知不等式是解决问题的关键,属中档题.
若函数 的值域为[0,+∞),则实数a的取值范围是( )
的值域为[0,+∞),则实数a的取值范围是( )
A.3>a≥2 B.3≥a>2 C.a≤2 D.a<2
知识点:2.定义域与值域
A
【考点】指数函数的定义、解析式、定义域和值域.
【专题】分类讨论;综合法;函数的性质及应用.
【分析】根据函数f(x)的解析式,求出x≤0时,f(x)的值域,再讨论x>0时,f(x)的值域,利用导数求出f(x)的最小值,由此求出a的取值范围.
【解答】解:∵函数 的值域为[0,+∞),
的值域为[0,+∞),
∴当x≤0时,0<2x≤1,∴1>1﹣2x≥0,
即0≤f(x)<1;
当x>0时,由f(x)=x3﹣3x+a,
∴f′(x)=3x2﹣3=3(x﹣1)(x+1),
∴当x∈(0,1)时,f′(x)<0,f(x)是减函数,
x∈(1,+∞)时,f′(x)>0,f(x)是增函数;
∴x=1时,f(x)取得最小值f(x)min=f(1)=1﹣3+a=a﹣2;
令0≤a﹣2<1,
解得2≤a<3.
故选:A.
【点评】本题考查了分段函数的应用问题,也考查了求函数的最值与值域的应用问题,是综合性题目.
已知函数f(x)的定义域为R,且f′(x)>1﹣f(x),f(0)=2,则不等式f(x)>1+e﹣x解集为( )
A.(﹣1,+∞) B.(e,+∞) C.(1,+∞) D.(0,+∞)
知识点:3.导数在研究函数中的应用
D
【考点】利用导数研究函数的单调性.
【专题】综合题;导数的概念及应用.
【分析】f(x)>1+e﹣x,等价于exf(x)﹣ex﹣1>0,设g(x)=exf(x)﹣ex﹣1,g(0)=0,则g(x)>g(0),确定g(x)是R上的增函数,即可得出结论.
【解答】解:∵f(x)>1+e﹣x,∴exf(x)﹣ex﹣1>0,
设g(x)=exf(x)﹣ex﹣1,
∵f′(x)>1﹣f(x),ex>0,
∴g′(x)=ex[f(x)+f′(x)﹣1]>0,
∴g(x)是R上的增函数,
又g(0)=0,则g(x)>g(0)
∴x>0,
故选:D.
【点评】本题考查导数知识的运用,考查函数的单调性,正确转化,构造函数,利用函数的单调性是关键.
已知正项等比数列{an}的前n项和为Sn,且S1,S3,S4成等差数列,则数列{an}的公比为 .
知识点:5.等比数列的前n项和

【考点】等比数列的性质;等差数列的性质.
【专题】分类讨论;方程思想;综合法;等差数列与等比数列.
【分析】设正项等比数列{an}的公比为q,由于S1,S3,S4成等差数列,可得2S3=S1+S4,q=1不成立,可得 =a1+
=a1+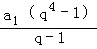 ,化简解出即可.
,化简解出即可.
【解答】解:设正项等比数列{an}的公比为q,
∵S1,S3,S4成等差数列,
∴2S3=S1+S4,
q=1不成立,
∴ =a1+
=a1+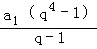 ,
,
化为q3﹣2q2+1=0,
(q﹣1)(q2﹣q﹣1)=0,q≠1,q>0,
解得q= .
.
故答案为: .
.
【点评】本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.
在△ABC中,内角A,B,C所对的边分别是a,b,c,若 ,则边长b的等于 .
,则边长b的等于 .
知识点:9.正弦定理和余弦定理(解三角形)
4
【考点】正弦定理的应用.
【专题】解三角形.
【分析】由已知条件利用正弦定理得ba=2cb,从而得到c=2,由此利用余弦定理能求出边长b的值.
【解答】解:在△ABC中,内角A,B,C所对的边分别是a,b,c,
∵ ,
,
∴ba=2cb,从而a=2c,又a=4,所以c=2,
∴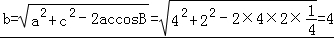 .
.
故答案为:4.
【点评】本题考查三角形的边长的求法,是中档题,解题时要认真审题,注意正弦定理和余弦定理的合理运用.
已知圆O上三个不同点A,B,C,若 ,则∠ACB= .
,则∠ACB= .
知识点:5.平面向量应用举例

【考点】向量在几何中的应用.
【专题】计算题;平面向量及应用.
【分析】由题意,向量式右边两个系数之和为1,所以A、B、O三点共线,即可得出结论.
【解答】解:由题意,向量式右边两个系数之和为1,所以A、B、O三点共线,
所以∠ACB= ,
,
故答案为: .
.
【点评】本题考查向量共线定理的运用,考查学生的计算能力,确定A、B、O三点共线是关键.
在△ABC中,a,b,c分别为内角A,B,C的对边,三边a,b,c成等差数列,且 ,则(cosA﹣cosC)2的值为 .
,则(cosA﹣cosC)2的值为 .
知识点:2.等差数列及其性质
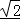
【考点】等差数列的性质.
【专题】等差数列与等比数列.
【分析】由题意可得a+c=2b,由正弦定理可得 ,进而由三角函数公式可得.
,进而由三角函数公式可得.
【解答】解:∵a,b,c成等差数列,∴a+c=2b,
由正弦定理可得 ,
,
∵(cosA﹣cosC)2+(sinA+sinC)2=2﹣2cos(A+C),
∴ ,
,
故答案为: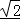 .
.
【点评】本题考查等差数列的性质,涉及正弦定理和三角函数公式,属中档题.
已知正项数列{an}的前n项和为Sn,且Sn是 和an的等差中项.
和an的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ,且
,且 成等比数列,当k1=2,k2=4时,求数列{kn}的前n项和Tn.
成等比数列,当k1=2,k2=4时,求数列{kn}的前n项和Tn.
知识点:2.等差数列及其性质
【考点】数列的求和;等差数列与等比数列的综合.
【专题】等差数列与等比数列.
【分析】(Ⅰ)由Sn是 和an的等差中项,可得
和an的等差中项,可得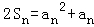 ,利用递推关系与等差数列的通项公式即可得出.
,利用递推关系与等差数列的通项公式即可得出.
(II)设等比数列的公比为q,由题意知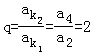 ,
,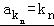 ,又
,又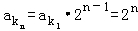 ,
,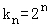 ,即可得出.
,即可得出.
【解答】解:(Ⅰ)∵Sn是 和an的等差中项,∴
和an的等差中项,∴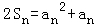 ,
,
又 ,
,
两式相减并化简得(an﹣an﹣1﹣1)(an+an﹣1)=0,
又an+an﹣1>0,所以an﹣an﹣1=1,故数列{an}是公差为1的等差数列,
当n=1时,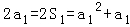 ,又a1>0,∴a1=1.
,又a1>0,∴a1=1.
∴an=1+(n﹣1)=n.
(Ⅱ)设等比数列的公比为q,由题意知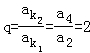 ,
,
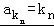 ,又
,又 ,
,
 ,
,
 .
.
【点评】本题考查了递推关系、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.
某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表
优秀
非优秀
合计
甲班
10
40
50
乙班
20
30
50
合计
30
70
100
(Ⅰ)根据列联表的数据,判断是否有99%的把握认为“成绩与班级有关系”;
(Ⅱ)若按下面的方法从甲班优秀的学生中抽取一人:把甲班10名优秀学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到8号的概率.
参考公式与临界值表:K2= .
.
P(K2≥k)
0.100
0.050
0.025
0.010
0.001
k
2.706
3.841
5.024
6.635
10.828
知识点:5.独立性检验的基本思想及其初步运用
【考点】独立性检验的应用.
【专题】概率与统计.
【分析】(Ⅰ)利用公式,求出K2,与临界值表比较后,即可得出结论;
(Ⅱ)所有的基本事件有:6×6=36个,出现点数之和为8的基本事件有5个,即可求出现点数之和为8的概率.
【解答】解:(Ⅰ)由题意可得:
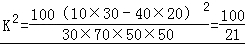 …
…
因为K2<6.635,所以没有99%的把握认为“成绩与班级有关系”…
(Ⅱ)先后两次抛掷一枚均匀的骰子,共有36种情况,…
出现点数之和为8的有以下5种(2,6),(3,5),(4,4),(5,3),(6,2)…
抽到8号的概率为 …
…
【点评】本题考查独立性检验的应用,考查概率的计算,考查学生的计算能力,比较基础
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)求证:PM∥平面AFC.

知识点:5.直线、平面平行的判定及其性质
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【专题】证明题;空间位置关系与距离.
【分析】(Ⅰ)矩形ABCD所在的平面和平面ABEF互相垂直,CB⊥AB,所以可推断出CB⊥平面ABEF,又AF⊂平面BDC1,所以CB⊥AF,进而由余弦定理求得BF,推断出AF2+BF2=AB2得AF⊥BF同时利用AF∩CB=B判断出AF⊥平面CFB,即可证明平面ADF⊥平面CBF;
(Ⅱ)连结OM延长交BF于H,则H为BF的中点,又P为CB的中点,推断出PH∥CF,又利用线面判定定理推断出PH∥平面AFC,连结PO,同理推断出PO∥平面AFC,利用面面平行的判定定理,推断出平面POO1∥平面AFC,最后利用面面平行的性质推断出PM∥平面AFC
【解答】证明:(Ⅰ)∵矩形ABCD所在的平面和平面ABEF互相垂直,CB⊥AB
∴CB⊥平面ABEF,
又AF⊂平面BDC1,∴CB⊥AF
又AB=2,AF=1,∠BAF=60°,
由余弦定理知BF= ,AF2+BF2=AB2得AF⊥BF
,AF2+BF2=AB2得AF⊥BF
∵AF∩CB=B,∴AF⊥平面CFB
∵AF⊂平面AFC,
∴平面ADF⊥平面CBF;
(Ⅱ)连结OM延长交BF于H,则H为BF的中点,又P为CB的中点,
∴PH∥CF,又∵AF⊂平面AFC,
∴PH∥平面AFC
连结PO,则PO∥AC,AC⊂平面AFC,PO∥平面AFC
PO∩PO1=P,
∴平面POO1∥平面AFC,
PM⊂平面AFC,
∴PM∥平面AFC.

【点评】本题主要考查了面面垂直的判定,线面平行的判定,面面平行的判定,以及线面垂直的性质,属于中档题.
己知抛物线C1:x2=2py(p>0)与圆C2:x2+y2=5的两个交点之间的距离为4.
(Ⅰ)求p的值;
(Ⅱ)设过抛物线C1的焦点F且斜率为k的直线与抛物线交于A,B两点,与圆C2交于C,D两点,当k∈[0,1]时,求|AB|•|CD|的取值范围.
知识点:4.直线与圆的位置关系
【考点】抛物线的简单性质.
【专题】综合题;圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)利用圆C1:x2+y2=5与抛物线C2:x2=2py(p>0)在第一象限内的交点为R(2,m),即可求m的值及抛物线C2的方程;
(Ⅱ)直线的方程为y=kx+1,分别于抛物线、圆的方程联立,求出|AB|,|CD|,利用k∈[0,1]时,即可求|AB|•|CD|的取值范围.
【解答】解:(Ⅰ)由题意,设抛物线C1:x2=2py(p>0)与圆C2:x2+y2=5在第一象限内的交点为R(2,m),
∴4+m2=5,
∵m>0,
∴m=1,
将(2,1)代入x2=2py,可得p=2;
(Ⅱ)抛物线C1的方程为x2=4y.直线的方程为y=kx+1,
联立x2=4y可得x2﹣4kx﹣4=0,
设A(x1,y1),B(x2,y2)
∴x1+x2=﹣4k,x1x2=﹣4
联立x2+y2=5可得(1+k2)x2+2kx﹣4=0,
设C(x3,y3),D(x4,y4),
∴x3+x4=﹣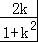 ,x3x4=﹣
,x3x4=﹣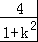 ,
,
∴|AB|= •
•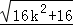 =16(1+k2),|CD|=
=16(1+k2),|CD|= ,
,
∴|AB||CD|=16 =
=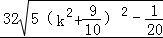 ,
,
∵k∈[0,1],∴k2∈[0,1],
∴|AB||CD|∈[64,96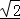 ].
].
【点评】本题考查抛物线方程,考查直线与抛物线、圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.
已知函数f(x)=alnx﹣x+2,其中a≠0.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若对任意的x1∈[1,e],总存在x2∈[1,e],使得f(x1)+f(x2)=4,求实数a值.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.
【专题】导数的综合应用.
【分析】(Ⅰ)先求出函数f(x)的导数,通过讨论①当a<0时,②当a>0时的情况,从而求出函数的单调区间;
(Ⅱ)通过讨论a的范围,结合函数的单调性找到函数的最值,从而求出a的值.
【解答】解:(Ⅰ)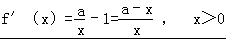 ,
,
当a<0时,对∀x∈(0,+∞),f′(x)<0,所以 f(x)的单调递减区间为(0,+∞);
当a>0时,令f′(x)=0,得x=a,
因为 x∈(0,a)时,f′(x)>0;x∈(a,+∞)时,f′(x)<0,
所以 f(x)的单调递增区间为(0,a),单调递减区间为(a,+∞).
(Ⅱ)用f(x)max,f(x)min分别表示函数f(x)在[1,e]上的最大值,最小值,
当a≤1且a≠0时,由(Ⅰ)知:在[1,e]上,f(x)是减函数,
所以 f(x)max=f(1)=1;
因为 对任意的x1∈[1,e],x2∈[1,e],f(x1)+f(x2)≤2f(1)=2<4,
所以对任意的x1∈[1,e],不存在x2∈[1,e],使得f(x1)+f(x2)=4;
当1<a<e时,由(Ⅰ)知:在[1,a]上,f(x)是增函数,在[a,e]上,f(x)是减函数,
所以 f(x)max=f(a)=alna﹣a+2;
因为 对x1=1,∀x2∈[1,e],f(1)+f(x2)≤f(1)+f(a)=1+alna﹣a+2=a(lna﹣1)+3<3,
所以 对x1=1∈[1,e],不存在x2∈[1,e],使得f(x1)+f(x2)=4;
当a≥e时,令g(x)=4﹣f(x)(x∈[1,e]),
由(Ⅰ)知:在[1,e]上,f(x)是增函数,进而知g(x)是减函数,
所以 f(x)min=f(1)=1,f(x)max=f(e)=a﹣e+2,g(x)max=g(1)=4﹣f(1),g(x)min=g(e)=4﹣f(e);
因为 对任意的x1∈[1,e],总存在x2∈[1,e],使得f(x1)+f(x2)=4,即f(x1)=g(x2),
所以  即
即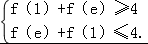 ,
,
所以 f(1)+f(e)=a﹣e+3=4,解得a=e+1,
综上所述,实数a的值为e+1.
【点评】本题考查了函数的单调性,函数的最值问题,考查导数的应用,分类讨论思想,是一道难题.
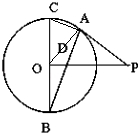
如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.
(1)证明:PA=PD;
(2)求证:PA•AC=AD•OC.

知识点:1.几何证明选讲
【考点】与圆有关的比例线段.
【专题】直线与圆.
【分析】(1)连结OA,由已知条件推导出∠PAD=∠PDA,即可证明PA=PD.
(2)连结OA,由已知条件推导出△PAD∽△OCA,由此能证明PA•AC=AD•OC.
【解答】(1)证明:连结AC,
∵直径BC⊥OP,连接AB交PO于点D,BC是直径,
∴∠C+∠B=90°,∠ODB+∠B=90°,
∴∠C=∠ODB,
∵直线PA为圆O的切线,切点为A,
∴∠C=∠BAP,
∵∠ADP=∠ODB,∴∠BAP=∠ADP,
∴PA=PD.
(2)连结OA,由(1)得∠PAD=∠PDA=∠ACO,
∵∠OAC=∠ACO,∴△PAD∽△OCA,
∴ ,∴PA•AC=AD•OC.
,∴PA•AC=AD•OC.
【点评】本题考查线段相等的证明,考查线段乘积相等的证明,是中档题,解题时要认真审题,注意弦切角定理的合理运用.
在平面直角坐标系xoy中,圆C的参数方程为 (t为参数).在极坐标系(与平面直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为
(t为参数).在极坐标系(与平面直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为 .
.
(Ⅰ)求圆C的普通方程及直线l的直角坐标方程;
(Ⅱ)设直线l被圆C截得的弦长为 ,求m的值.
,求m的值.
知识点:2.坐标系与参数方程
【考点】圆的参数方程;简单曲线的极坐标方程.
【专题】坐标系和参数方程.
【分析】(Ⅰ)把圆的参数方程变形,平方后相加可得圆的普通方程,把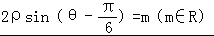 左边展开两角差的正弦,代入x=ρcosθ,y=ρsinθ得答案;
左边展开两角差的正弦,代入x=ρcosθ,y=ρsinθ得答案;
(Ⅱ)由直线l被圆C截得的弦长为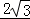 ,圆的半径为2,可得圆心到直线的距离,由点到直线的距离公式求得m的值.
,圆的半径为2,可得圆心到直线的距离,由点到直线的距离公式求得m的值.
【解答】解:(Ⅰ)由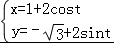 ,得
,得 ,两式平方相加得:
,两式平方相加得: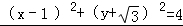 ,
,
∴圆C的普通方程为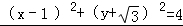 ;
;
由 ,
,
从而得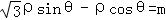 ,∴
,∴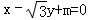 ;
;
(Ⅱ)∵直线l被圆C截得的弦长为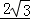 ,且圆的半径为2,
,且圆的半径为2,
∴圆心到直线的距离为1,
即 ,
,
从而得|m+4|=2,解得m=﹣2或﹣6.
【点评】本题考查参数方程化普通方程,考查了极坐标方程化直角坐标方程,考查弦心距、弦长及圆的半径间的关系的运用,是中档题.
已知函数f(x)=|1﹣2x|﹣|1+x|
(Ⅰ)解不等式f(x)≥4;
(Ⅱ)若函数g(x)=|1+x|+a的图象恒在函数f(x)的图象的上方,求实数a的取值范围.
知识点:3.不等式选讲
【考点】带绝对值的函数.
【专题】函数的性质及应用;不等式的解法及应用.
【分析】(Ⅰ)运用分类讨论的思想方法,去绝对值,即可得到不等式组,即可得到所求解集;
(Ⅱ)由题意可得不等式a>|1﹣2x|﹣2|1+x|恒成立,由绝对值不等式的性质,可得右边函数的最大值,进而得到a的范围.
【解答】解:(Ⅰ)不等式f(x)≥4化为f(x)=|1﹣2x|﹣|1+x|≥4,则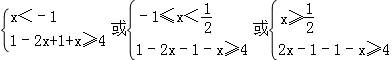
解得x≤﹣2,或x≥6,
所以不等式的解集为{x|x≤﹣2,或x≥6};
(Ⅱ)∵函数g(x)=|1+x|+a的图象恒在函数f(x)的图象的上方,
∴|1+x|+a>|1﹣2x|﹣|1+x|,
即不等式a>|1﹣2x|﹣2|1+x|恒成立,
令h(x)=|1﹣2x|﹣2|1+x|=|1﹣2x|﹣|2+2x|
由||1﹣2x|﹣|2+2x||≤|(1﹣2x)+(2+2x)|=3,
得h(x)max=3,
所以实数a的取值范围a>3.
【点评】本题考查绝对值不等式的性质,以及不等式恒成立思想,注意运用参数分离和分类讨论的思想方法,属于中档题.