点M的直角坐标( ,﹣1)化成极坐标为( )
,﹣1)化成极坐标为( )
A.(2, ) B.(2,
) B.(2, ) C.(2,
) C.(2, ) D.(2,
) D.(2, )
)
知识点:2.坐标系与参数方程
D
【考点】Q6:极坐标刻画点的位置.
【分析】根据x=ρcosθ,y=ρsinθ,可得极坐标.
【解答】解:点M的直角坐标(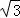 ,﹣1)
,﹣1)
由x=ρcosθ,y=ρsinθ,
∴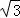 =ρcosθ,﹣1=ρsinθ,
=ρcosθ,﹣1=ρsinθ,
解得:ρ=2,θ=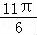 ,
,
∴极坐标为(2,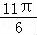 )
)
故选D.
圆的极坐标方程为ρ=2(cosθ+sinθ),则该圆的圆心极坐标是( )
A. B.(
B.( ,
, ) C.(
) C.( ,
, ) D.
) D.
知识点:2.坐标系与参数方程
B
【考点】Q4:简单曲线的极坐标方程.
【分析】由极坐标方程求出圆的直角坐标方程,从而求出该圆的圆心平面直角坐标,由此能求出该圆的圆心极坐标.
【解答】解:∵极坐标方程为ρ=2(cosθ+sinθ),
∴ρ2=2ρcosθ+2ρsinθ,
∴x2+y2=2x+2y,
∴x2+y2﹣2x﹣2y=0,
∴该圆的圆心平面直角坐标为(1,1),
∴该圆的圆心极坐标为(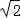 ,
,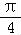 ).
).
故选:B.
曲线C的参数方程为 ,则它的普通方程为( )
,则它的普通方程为( )
A.y=x2+1 B.y=﹣x2+1
C. D.y=x2+1,x∈[﹣
D.y=x2+1,x∈[﹣ ,
, ]
]
知识点:2.坐标系与参数方程
C
【考点】QH:参数方程化成普通方程.
【分析】将第1个方程两边平方,加上第2个方程,可得y=﹣x2+1,结合x的范围,即可得出结论.
【解答】解:将第1个方程两边平方,加上第2个方程,可得y=﹣x2+1,
又x=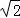 sin(α+
sin(α+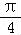 )∈[﹣
)∈[﹣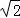 ,
,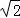 ],
],
∴普通方程为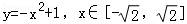 .
.
故选:C.
在极坐标系中,O为极点, ,
, ,则S△AOB=( )
,则S△AOB=( )
A.2 B.3 C.4 D.5
知识点:2.坐标系与参数方程
D
【考点】Q4:简单曲线的极坐标方程.
【分析】∠AOB=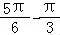 =
= .利用直角三角形面积计算公式即可得出.
.利用直角三角形面积计算公式即可得出.
【解答】解:∠AOB=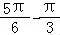 =
= .
.
∴S△AOB=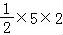 =5.
=5.
故选:D.
已知ab≠0,点M(a,b)是圆x2+y2=r2内一点,直线m是以点M为中点的弦所在的直线,直线l的方程是ax+by=r2,则下列结论正确的是( )
A.m∥l,且l与圆相交 B.l⊥m,且l与圆相切
C.m∥l,且l与圆相离 D.l⊥m,且l与圆相离
知识点:4.直线与圆的位置关系
C
【考点】J9:直线与圆的位置关系.
【分析】求圆心到直线的距离,然后与a2+b2<r2比较,可以判断直线与圆的位置关系,易得两直线的关系.
【解答】解:以点M为中点的弦所在的直线的斜率是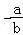 ,直线m∥l,点M(a,b)是圆x2+y2=r2内一点,所以a2+b2<r2,圆心到ax+by=r2,距离是
,直线m∥l,点M(a,b)是圆x2+y2=r2内一点,所以a2+b2<r2,圆心到ax+by=r2,距离是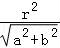 >r,故相离.
>r,故相离.
故选C.
两圆相交于两点(k,1)和(1,3),两圆的圆心都在直线x﹣y+ =0上,则k+c=( )
=0上,则k+c=( )
A.﹣1 B.2 C.3 D.0
知识点:4.直线与圆的位置关系
C
【考点】JE:直线和圆的方程的应用.
【分析】由相交弦的性质,可得AB与直线x﹣y+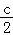 =0垂直,且AB的中点在这条直线x﹣y+
=0垂直,且AB的中点在这条直线x﹣y+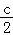 =0上;由AB与直线x﹣y+
=0上;由AB与直线x﹣y+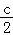 =0垂直,可得为﹣1,解可得k的值,即可得A的坐标,进而可得AB中点的坐标,代入直线方程可得c=0;进而将k、c相加可得答案.
=0垂直,可得为﹣1,解可得k的值,即可得A的坐标,进而可得AB中点的坐标,代入直线方程可得c=0;进而将k、c相加可得答案.
【解答】解:根据题意,由相交弦的性质,相交两圆的连心线垂直平分相交弦,设A(k,1)和B(1,3),
可得AB与直线x﹣y+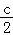 =0垂直,且AB的中点在这条直线x﹣y+
=0垂直,且AB的中点在这条直线x﹣y+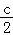 =0上;
=0上;
由AB与直线x﹣y+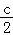 =0垂直,可得
=0垂直,可得 =﹣1,解可得k=3,
=﹣1,解可得k=3,
则A(3,1),
故AB中点为(2,2),且其在直线x﹣y+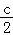 =0上,
=0上,
代入直线方程可得,2﹣2+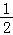 c=0,可得c=0;
c=0,可得c=0;
故k+c=3;
故选:C.
若函数 在[1,+∞)上是单调函数,则a的取值范围是( )
在[1,+∞)上是单调函数,则a的取值范围是( )
A. B.
B. C.
C. D.(﹣∞,1]
D.(﹣∞,1]
知识点:3.导数在研究函数中的应用
B
【考点】6B:利用导数研究函数的单调性.
【分析】由求导公式和法则求出f′(x),由条件和导数与函数单调性的关系分类讨论,分别列出不等式进行分离常数,再构造函数后,利用整体思想和二次函数的性质求出函数的最值,可得a的取值范围.
【解答】解:由题意得,f′(x)=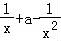 ,
,
因为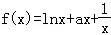 在[1,+∞)上是单调函数,
在[1,+∞)上是单调函数,
所以f′(x)≥0或f′(x)≤0在[1,+∞)上恒成立,
①当f′(x)≥0时,则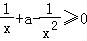 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a≥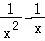 ,设g(x)=
,设g(x)=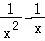 =
=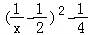 ,
,
因为x∈[1,+∞),所以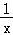 ∈(0,1],
∈(0,1],
当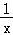 =1时,g(x)取到最大值是:0,
=1时,g(x)取到最大值是:0,
所以a≥0,
②当f′(x)≤0时,则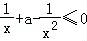 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a≤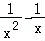 ,设g(x)=
,设g(x)=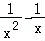 =
=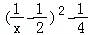 ,
,
因为x∈[1,+∞),所以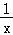 ∈(0,1],
∈(0,1],
当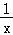 =
=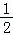 时,g(x)取到最大值是:
时,g(x)取到最大值是: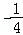 ,
,
所以a≤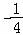 ,
,
综上可得,a≤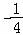 或a≥0,
或a≥0,
所以数a的取值范围是(﹣∞,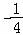 ]∪[0,+∞),
]∪[0,+∞),
故选:B.
已知下表所示数据的回归直线方程为 ,则实数a的值为( )
,则实数a的值为( )
x
2
3
4
5
6
y
3
7
11
a
21
A.16 B.18 C.20 D.22
知识点:4.回归分析的基本思想及其初步应用
B
【考点】BK:线性回归方程.
【分析】由表中数据计算样本中心点的横坐标,根据回归直线经过样本中心点求出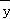 的值,从而求出a的值.
的值,从而求出a的值.
【解答】解:由表中数据知,样本中心点的横坐标为:
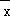 =
= ×(2+3+4+5+6)=4,
×(2+3+4+5+6)=4,
由回归直线经过样本中心点,
得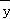 =4×4﹣4=12,
=4×4﹣4=12,
即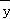 =
= ×(3+7+11+a+21)=12,
×(3+7+11+a+21)=12,
解得a=18.
故选:B.
函数 ,则( )
,则( )
A.x=e为函数f(x)的极大值点 B.x=e为函数f(x)的极小值点
C. 为函数f(x)的极大值点 D.
为函数f(x)的极大值点 D. 为函数f(x)的极小值点
为函数f(x)的极小值点
知识点:3.导数在研究函数中的应用
A
【考点】6D:利用导数研究函数的极值.
【分析】求导,令f′(x)>0,求得函数的单调递增区间,令f′(x)<0,求得函数的单调递减区间,则当x=e时,函数有极大值.
【解答】解: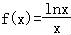 的定义域(0,+∞),求导f′(x)=
的定义域(0,+∞),求导f′(x)=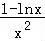 ,
,
令f′(x)=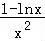 >0,解得:0<x<e,令f′(x)=
>0,解得:0<x<e,令f′(x)=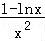 <0,解得:x>e,
<0,解得:x>e,
∴函数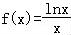 在(0,e)上递增,在(e,+∞)上递减,
在(0,e)上递增,在(e,+∞)上递减,
∴当x=e时,函数有极大值,
故选A.
已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:2(k﹣3)x﹣2y+3=0平行,则k的值是( )
A.1或3 B.1或5 C.3或5 D.1或2
知识点:1.直线的倾斜角、斜率与方程
C
【考点】II:直线的一般式方程与直线的平行关系.
【分析】当k﹣3=0时,求出两直线的方程,检验是否平行;当k﹣3≠0时,由一次项系数之比相等且不等于常数项之比,求出k的值.
【解答】解:由两直线平行得,当k﹣3=0时,两直线的方程分别为 y=﹣1 和 y=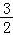 ,显然两直线平行.
,显然两直线平行.
当k﹣3≠0时,由  =
=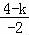 ≠
≠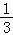 ,可得 k=5.综上,k的值是 3或5,
,可得 k=5.综上,k的值是 3或5,
故选 C.
点A(2,1)到抛物线y2=ax准线的距离为1,则a的值为( )
A. 或
或 B.
B. 或
或 C.﹣4或﹣12 D.4或12
C.﹣4或﹣12 D.4或12
知识点:3.抛物线
C
【考点】K8:抛物线的简单性质.
【分析】求出抛物线的准线方程,根据距离列出方程解出a的值.
【解答】解:抛物线的准线方程为x=﹣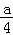 ,
,
∴点A(2,1)到抛物线y2=ax准线的距离为|2+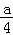 |=1
|=1
解得a=4或a=﹣12.
故选C.
如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )

A. B.
B. C.
C. D.
D.
知识点:1.椭圆
A
【考点】NF:平面与圆柱面的截线.
【分析】利用已知条件,求出题意的长半轴,短半轴,然后求出半焦距,即可求出题意的离心率.
【解答】解:因为底面半径为R的圆柱被与底面成30°的平面所截,其截口是一个椭圆,
则这个椭圆的短半轴为:R,长半轴为: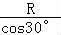 =
=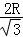 ,
,
∵a2=b2+c2,∴c=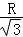 ,
,
∴椭圆的离心率为:e=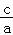 =
=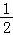 .
.
故选:A.
设点M的柱坐标为( ,
, ,
, ),则其直角坐标是 .
),则其直角坐标是 .
知识点:2.坐标系与参数方程
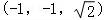
【考点】QB:柱坐标刻画点的位置.
【分析】设点M的直角坐标为(x,y,z),根据变换公式为 ,得x=
,得x=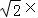
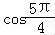 ,y=
,y=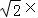 sin
sin ,z=
,z=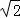 解出其坐标值即可.
解出其坐标值即可.
【解答】解:由题意:∵M点的柱面坐标为M(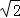 ,
,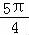 ,
,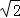 ),设点M的直角坐标为(x,y,z),
),设点M的直角坐标为(x,y,z),
∴x=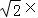
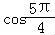 ,y=
,y=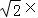 sin
sin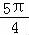 ,z=
,z=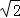
解得x=﹣1,y=﹣1,z=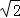 .
.
∴M点的直角坐标为:M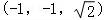 .
.
故答案为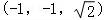 .
.
设曲线C的参数方程为 (θ为参数),直线l的方程为x﹣3y+2=0,则曲线C上到直线l的距离为
(θ为参数),直线l的方程为x﹣3y+2=0,则曲线C上到直线l的距离为 的点的个数为 个.
的点的个数为 个.
知识点:2.坐标系与参数方程
4
【考点】QH:参数方程化成普通方程.
【分析】由题意将圆C和直线l先化为一般方程坐标,然后再计算曲线C上到直线l距离为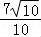 的点的个数.
的点的个数.
【解答】解:化曲线C的参数方程为普通方程:(x﹣2)2+(y﹣1)2=9,
圆心(2,1)到直线x﹣3y+2=0的距离d= =
=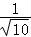 <3,
<3,
直线和圆相交,过圆心和l平行的直线和圆的2个交点符合要求,
又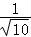 +
+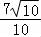 <3
<3
在直线l的另外一侧有圆上的2个点符合要求,
故答案为4
在同一平面直角坐标系中,直线x﹣2y=2经过伸缩变换 变成直线l,则直线l的方程是 .
变成直线l,则直线l的方程是 .
知识点:2.坐标系与参数方程
x﹣y﹣2=0.
【考点】QH:参数方程化成普通方程.
【分析】由伸缩变换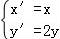 可得:
可得: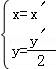 ,代入直线x﹣2y=2即可得出.
,代入直线x﹣2y=2即可得出.
【解答】解:由伸缩变换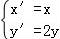 可得:
可得: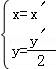 ,
,
代入直线x﹣2y=2可得:x′﹣2× =2,即x﹣y﹣2=0.
=2,即x﹣y﹣2=0.
故直线l的方程是:x﹣y﹣2=0.
故答案为:x﹣y﹣2=0.
已知函数f(x)=lnx﹣3x,则曲线y=f(x)在点(1,f(1))处的切线方程是 .
知识点:1.变化率与导数
2x+y+1=0
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】求出曲线的导函数,把x=1代入即可得到切线的斜率,然后根据(1,﹣3)和斜率写出切线的方程即可.
【解答】解:由函数f(x)=lnx﹣3x知f′(x)=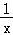 ﹣3,把x=1代入得到切线的斜率k=﹣2,
﹣3,把x=1代入得到切线的斜率k=﹣2,
∵f(1)=﹣3,
∴切线方程为:y+3=﹣2(x﹣1),即2x+y+1=0.
故答案为2x+y+1=0
直线l交椭圆 +y2=1于A,B两点,若线段AB的中点坐标为(1,
+y2=1于A,B两点,若线段AB的中点坐标为(1, ).则直线l的方程为 .
).则直线l的方程为 .
知识点:1.椭圆
2x+2y﹣3=0
【考点】KL:直线与椭圆的位置关系.
【分析】设A(x1,y1),B(x2,y2).由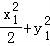 =1,
=1,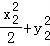 =1,相减可得:
=1,相减可得: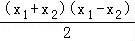 +(y1+y2)(y1﹣y2)=0,利用中点坐标公式、斜率计算公式代入即可得出.
+(y1+y2)(y1﹣y2)=0,利用中点坐标公式、斜率计算公式代入即可得出.
【解答】解:设A(x1,y1),B(x2,y2).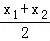 =1,
=1,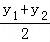 =
=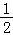 .k=
.k=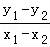 .
.
由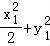 =1,
=1,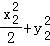 =1,相减可得:
=1,相减可得: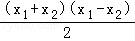 +(y1+y2)(y1﹣y2)=0,
+(y1+y2)(y1﹣y2)=0,
∴1+k=0,解得k=﹣1.
∴直线l的方程为:y﹣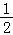 =﹣(x﹣1),化为:2x+2y﹣3=0.
=﹣(x﹣1),化为:2x+2y﹣3=0.
故答案为:2x+2y﹣3=0.
一个盒子中装有2个红球,4个白球,除颜色外,它们的形状、大小、质量等完全相同
(1)采用不放回抽样,先后取两次,每次随机取一个球,求恰好取到1个红球,1个白球的概率;
(2)采用放回抽样,每次随机抽取一球,连续取3次,求至少有1次取到红球的概率.
知识点:5.条件概率与相互独立事件同时发生的概率
【考点】CB:古典概型及其概率计算公式.
【分析】(1)利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出恰好取到1个红球,1个白球的概率.
(2)采用放回抽样,每次取到红球的概率都是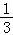 ,由此利用对立事件概率计算公式能求出至少有1次取到红球的概率.
,由此利用对立事件概率计算公式能求出至少有1次取到红球的概率.
【解答】解:(1)一个盒子中装有2个红球,4个白球,除颜色外,它们的形状、大小、质量等完全相同,
采用不放回抽样,先后取两次,每次随机取一个球,
恰好取到1个红球,1个白球的概率为:
p1=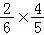 +
+ =
=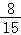 .
.
(2)采用放回抽样,每次取到红球的概率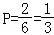 ,
,
∴至少有1次取到红球的概率为p2=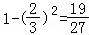 .
.
在极坐标系中,已知点 ,直线为
,直线为 .
.
(1)求点 的直角坐标与直线的普通方程;
的直角坐标与直线的普通方程;
(2)求点 到直线
到直线 的距离.
的距离.
知识点:2.坐标系与参数方程
【考点】Q4:简单曲线的极坐标方程.
【分析】(1)利用互化公式x=ρcosθ,y=ρsinθ即可把极坐标化为直角坐标.
(2)利用点到直线的距离公式即可得出.
【解答】解:(1)点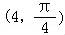 化成直角坐标为
化成直角坐标为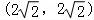 .
.
直线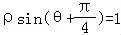 ,展开可得:
,展开可得: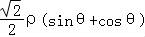 =1,可得:直角坐标方程为
=1,可得:直角坐标方程为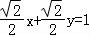 ,即
,即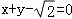 .
.
(2)由题意可知,点 到直线
到直线 的距离,由距离公式可得
的距离,由距离公式可得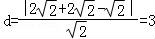 .
.
已知曲线C的参数方程为 (θ为参数),直线l的极坐标方程为ρsin(θ+
(θ为参数),直线l的极坐标方程为ρsin(θ+ )=2
)=2 .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)设点P为曲线C上的动点,求点P到直线l距离的最大值.
知识点:2.坐标系与参数方程
【考点】QH:参数方程化成普通方程.
【分析】第一问,利用平方关系消参,得到曲线C的普通方程,利用ρ2=x2+y2,x=ρcosθ,y=ρsinθ转化,得到直线l的直角坐标方程;第二问,利用点到直线的距离公式列出表达式,再利用两角和的正弦公式化简,求三角函数的最值即可得到结论.
【解答】解:(1)曲线C的参数方程为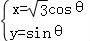 (θ为参数),消去θ可得曲线C的普通方程为
(θ为参数),消去θ可得曲线C的普通方程为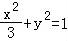 ,
,
直线l的极坐标方程为ρsin(θ+ )=2
)=2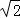 .即
.即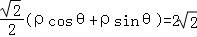
直线l的直角坐标方程为x+y﹣4=0.
(2)设点P坐标为(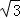 cosθ,sinθ),
cosθ,sinθ),
点P到直线l的距离d=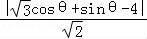 =
=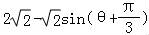
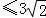 .
.
所以点P到直线l距离的最大值为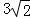 .
.
椭圆C的中心在坐标原点,焦点在x轴上,焦点到短轴端点的距离为2,离心率为 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线l与椭圆C交于A,B两点且OA⊥OB,是否存在以原点O为圆心的定圆与直线l相切?若存在求出定圆方程;若不存在,请说明理由.
知识点:1.椭圆
【考点】K4:椭圆的简单性质.
【分析】(Ⅰ)由题意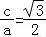 ,且a=2,由此能求出椭圆方程.
,且a=2,由此能求出椭圆方程.
(Ⅱ)设直线AB:y=kx+m,由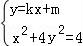 ,得(1+4k2)x2+8kmx+4m2﹣4=0,由此利用根的判别式、韦达定理、向量垂直、点到直线的距离公式,能求出定圆方程.
,得(1+4k2)x2+8kmx+4m2﹣4=0,由此利用根的判别式、韦达定理、向量垂直、点到直线的距离公式,能求出定圆方程.
【解答】解:(Ⅰ)设椭圆的半焦距为c,
∵椭圆C的中心在坐标原点,焦点在x轴上,焦点到短轴端点的距离为2,离心率为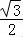 ,
,
∴由题意 ,且a=2,解得c=
,且a=2,解得c=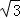 ,b=1.
,b=1.
∴所求椭圆方程为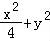 =1.…
=1.…
(Ⅱ)设A(x1,y1),B(x2,y2),若k存在,则设直线AB:y=kx+m,
由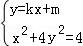 ,得(1+4k2)x2+8kmx+4m2﹣4=0,…
,得(1+4k2)x2+8kmx+4m2﹣4=0,…
∴△=64k2m2﹣4(1+4k2)(4m2﹣4)>0,且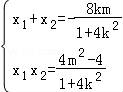 ,…
,…
由OA⊥OB,知x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=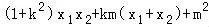 =0,代入得5m2=4k2+4,…
=0,代入得5m2=4k2+4,…
原点到直线AB的距离d=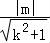 =
=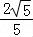 ,…
,…
当AB的斜率不存在时,|x1|=|y1|,得 =1,|x1|=
=1,|x1|=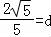 ,依然成立
,依然成立
∴点O到直线AB的距离为定值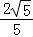 .…
.…
∴定圆方程为x2+y2=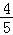 .…
.…
已知函数f(x)=a(x+lnx)(a≠0),g(x)=x2.
(1)若f(x)的图象在x=1处的切线恰好也是g(x)图象的切线.
①求实数a的值;
②若方程f(x)=mx在区间 内有唯一实数解,求实数m的取值范围.
内有唯一实数解,求实数m的取值范围.
(2)当0<a<1时,求证:对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)﹣f(x2)|<|g(x1)﹣g(x2)|成立.
知识点:3.导数在研究函数中的应用
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】(1)①求导数,利用f(x)的图象在x=1处的切线恰好也是g(x)图象的切线,求实数a的值;
②由x+lnx=mx,得m=1+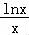 ,设t(x)=1+
,设t(x)=1+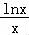 ,x∈
,x∈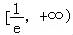 ,则问题等价于y=m与t(x)的图象在
,则问题等价于y=m与t(x)的图象在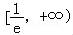 上有唯一交点,即可求实数m的取值范围.
上有唯一交点,即可求实数m的取值范围.
(2)设F(x)=f(x)﹣g(x),即F(x)=a(x+lnx)﹣x2,F(x)在[1,2]上单调递减,F′(x)=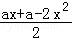 ≤0恒成立,即a≤
≤0恒成立,即a≤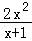 在[1,2]上恒成立,即可证明结论.
在[1,2]上恒成立,即可证明结论.
【解答】(1)解:①f′(x)=a(1+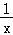 ),∴x=1,f′(x)=2a,切点为(1,a),
),∴x=1,f′(x)=2a,切点为(1,a),
∴切线方程为y﹣a=2a(x﹣1),即y=2ax﹣a,
联立 ,消去y,可得x2﹣2ax+a=0,△=4a2﹣4a=0,∴a=1;
,消去y,可得x2﹣2ax+a=0,△=4a2﹣4a=0,∴a=1;
②由x+lnx=mx,得m=1+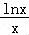 ,
,
设t(x)=1+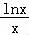 ,x∈
,x∈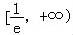 ,则问题等价于y=m与t(x)的图象在
,则问题等价于y=m与t(x)的图象在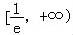 上有唯一交点,
上有唯一交点,
∵t′(x)=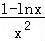 ,∴(
,∴(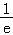 ,e),t′(x)>0,函数单调递增,(e,+∞),t′(x)<0,函数单调递减,
,e),t′(x)>0,函数单调递增,(e,+∞),t′(x)<0,函数单调递减,
∵t(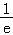 )=1﹣e,t(e)=1+
)=1﹣e,t(e)=1+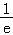 ,且x∈(e,+∞)时,t(x)>1,
,且x∈(e,+∞)时,t(x)>1,
∴m∈[1﹣e]∪{1+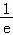 };
};
证明:(2)不妨设1≤x1<x2≤2,则f(x1)<f(x2),g(x1)<g(x2),
∴|f(x1)﹣f(x2)|<|g(x1)﹣g(x2)|可化为f(x2)﹣f(x1)<g(x2)﹣g(x1)
∴f(x2)﹣g(x2)<f(x1)﹣g(x1)
设F(x)=f(x)﹣g(x),即F(x)=a(x+lnx)﹣x2,∴F(x)在[1,2]上单调递减,
∴F′(x)=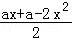 ≤0恒成立,即a≤
≤0恒成立,即a≤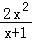 在[1,2]上恒成立,
在[1,2]上恒成立,
∵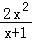 =
= ≥1,∴a≤1,
≥1,∴a≤1,
从而,当0<a<1时,命题成立.