设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|x2﹣5x+4<0},则(∁UA)∩(∁UB)=( )
A.{0,1,2,3} B.{5} C.{1,2,4} D.{0,4,5}
知识点:3.集合的基本运算
D
【考点】交、并、补集的混合运算.
【分析】化简集合B,根据补集与交集的定义进行计算即可.
【解答】解:全集U={0,1,2,3,4,5},集合A={1,2},
B={x|x2﹣5x+4<0,x∈U}={x|1<x<4,x∈U}={2,3},
∴∁UA={0,3,4,5},
∁UB={0,1,4,5},
∴集合(∁UA)∩(∁UB)={0,4,5}.
故选:D.
【点评】本题考查了集合的化简与运算问题,是基础题目.
已知复数z满足(z+i)(1﹣2i)=2,则复数z在复平面内的对应点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
知识点:3.复数代数形式的四则运算
D
【考点】复数代数形式的乘除运算.
【分析】把已知等式变形,利用复数代数形式的乘除运算化简得答案.
【解答】解:由(z+i)(1﹣2i)=2,得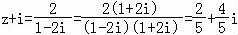 ,
,
∴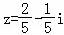 .
.
∴复数z在复平面内的对应点的坐标为(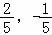 ),所在象限是第四象限.
),所在象限是第四象限.
故选:D.
【点评】本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.
已知α,β是两个不同平面,直线l⊂β,则“α∥β”是“l∥α”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
A
【考点】必要条件、充分条件与充要条件的判断.
【分析】α,β是两个不同平面,直线l⊂β,则“α∥β”⇒“l∥α”,反之不成立.即可得出结论.
【解答】解:∵α,β是两个不同平面,直线l⊂β,则“α∥β”⇒“l∥α”,反之不成立.
∴α,β是两个不同平面,直线l⊂β,则“α∥β”是“l∥α”的充分不必要条件.
故选:A.
【点评】本题考查了线面面面平行的判定与性质定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n等于( )

A.2 B.3 C.4 D.5
知识点:8.算法初步与框图
C
【考点】程序框图.
【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
【解答】解:当n=1时,a=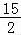 ,b=4,满足进行循环的条件,
,b=4,满足进行循环的条件,
当n=2时,a=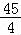 ,b=8满足进行循环的条件,
,b=8满足进行循环的条件,
当n=3时,a=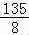 ,b=16满足进行循环的条件,
,b=16满足进行循环的条件,
当n=4时,a=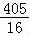 ,b=32不满足进行循环的条件,
,b=32不满足进行循环的条件,
故输出的n值为4,
故选C.
【点评】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.
设随机变量η服从正态分布N(1,σ2),若P(η<﹣1)=0.2,则函数 没有极值点的概率是( )
没有极值点的概率是( )
A.0.2 B.0.3 C.0.7 D.0.8
知识点:10.正态分布
C
【考点】正态分布曲线的特点及曲线所表示的意义;函数在某点取得极值的条件.
【分析】函数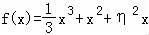 没有极值点,则f′(x)=x2+2x+η2=0无解,可得η的取值范围,再根据随机变量η服从正态分布N(1,σ2),可得曲线关于直线x=1对称,从而可得结论.
没有极值点,则f′(x)=x2+2x+η2=0无解,可得η的取值范围,再根据随机变量η服从正态分布N(1,σ2),可得曲线关于直线x=1对称,从而可得结论.
【解答】解:∵函数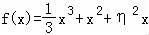 没有极值点,
没有极值点,
∴f′(x)=x2+2x+η2=0无解,
∴△=4﹣4η2<0,
∴η<﹣1或η>1,
∵随机变量η服从正态分布N(1,σ2),P(η<﹣1)=0.2,
∴P(η<﹣1或η>1)=0.2+0.5=0.7,
故选C.
【点评】本题考查函数的极值点,考查正态分布曲线的对称性,同时考查了运算求解的能力,属于中档题.
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
A.9+16π B.9+18π C.12+18π D.18+18π
知识点:3.空间几何体的表面积与体积
D
【考点】由三视图求面积、体积.
【分析】由三视图可知:该几何体是由上下两部分组成的,上面是一个倒立的四棱锥,下面是一个圆柱.
【解答】解:由三视图可知:该几何体是由上下两部分组成的,上面是一个倒立的四棱锥,下面是一个圆柱.
∴该几何体的体积=π×32×2+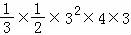
=18π+18.
故选:D.
【点评】本题考查了圆柱与圆锥的三视图及其体积计算公式,考查了推理能力与计算能力,属于中档题.
函数y=ln|x|﹣x2的图象大致为( )
A. B.
B. C.
C. D.
D.
知识点:15.函数的图像
A
【考点】函数的图象.
【分析】先判断函数为偶函数,再根据函数的单调性即可判断.
【解答】解:令y=f(x)=ln|x|﹣x2,其定义域为(﹣∞,0)∪(0,+∞),
因为f(﹣x)=ln|x|﹣x2=f(x),
所以函数y=ln|x|﹣x2为偶函数,其图象关于y轴对称,故排除B,D,
当x>0时,f(x)=lnx﹣x2,
所以f′(x)=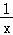 ﹣2x=
﹣2x= ,
,
当x∈(0,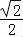 )时,f′(x)>0,函数f(x)递增,
)时,f′(x)>0,函数f(x)递增,
当x∈(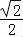 ,+∞)时,f′(x)<0,函数f(x)递减,
,+∞)时,f′(x)<0,函数f(x)递减,
故排除C,
方法二:当x→+∞时,函数y<0,故排除C,
故选:A
【点评】本题考查了函数的图象的识别,关键掌握函数的奇偶性和函数的单调性,属于中档题.
已知函数f(x)=sin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则( +
+ )•(
)•( ﹣
﹣ )的值为( )
)的值为( )

A.﹣1 B. C.
C. D.2
D.2
知识点:7.函数y=Asin(wx+@)+B
D
【考点】平面向量数量积的运算.
【分析】可求出f(x)的周期为2,从而得出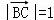 ,根据正弦函数的对称性可知,点C为DE的中点,从而
,根据正弦函数的对称性可知,点C为DE的中点,从而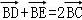 ,并且
,并且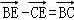 ,代入
,代入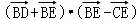 进行数量积的运算即可.
进行数量积的运算即可.
【解答】解:f(x)=sin(πx+φ)的周期为2;
∴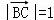 ;
;
D,E关于点C对称;
∴C是线段DE的中点;
∴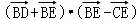
=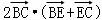
=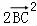
=2.
故选D.
【点评】考查三角函数周期的计算公式,正弦函数的对称中心,以及向量加法的平行四边形法则,向量加法的几何意义.
等差数列{an}的前n项和为Sn,若公差d>0,(S8﹣S5)(S9﹣S5)<0,则( )
A.|a7|>|a8| B.|a7|<|a8| C.|a7|=|a8| D.|a7|=0
知识点:3.等差数列的前n项和
B
【考点】等差数列的性质.
【分析】根据题意,由(S8﹣S5)(S9﹣S5)<0分析可得(a6+a7+a8)(a6+a7+a8+a9)<0,结合等差数列的性质可得(a6+a7+a8)(a6+a7+a8+a9)<0⇔a7×(a7+a8)<0,
又由{an}的公差d>0,分析可得a7<0,a8>0,且|a7|<|a8|;即可得答案.
【解答】解:根据题意,等差数列{an}中,有(S8﹣S5)(S9﹣S5)<0,
即(a6+a7+a8)(a6+a7+a8+a9)<0,
又由{an}为等差数列,则有(a6+a7+a8)=3a7,(a6+a7+a8+a9)=2(a7+a8),
(a6+a7+a8)(a6+a7+a8+a9)<0⇔a7×(a7+a8)<0,
a7与(a7+a8)异号,
又由公差d>0,
必有a7<0,a8>0,且|a7|<|a8|;
故选:B.
【点评】本题考查等差数列的性质,关键是由(S8﹣S5)(S9﹣S5)<0,分析得到a7、a8之间的关系.
长方体ABCD﹣A1B1C1D1中, ,点N是平面A1B1C1D1上的点,且满足
,点N是平面A1B1C1D1上的点,且满足 ,当长方体ABCD﹣A1B1C1D1的体积最大时,线段MN的最小值是( )
,当长方体ABCD﹣A1B1C1D1的体积最大时,线段MN的最小值是( )
A. B.8 C.
B.8 C. D.
D.
知识点:3.空间几何体的表面积与体积
C
【考点】棱柱的结构特征.
【分析】由题意,当长方体ABCD﹣A1B1C1D1的体积最大时,长方体ABCD﹣A1B1C1D1为棱长为4的正方体.N的轨迹是平面A1B1C1D1中,以C1为圆心,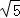 为半径的圆的
为半径的圆的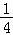 ,设M在平面A1B1C1D1中的射影为O,则O为A1B1的中点,ON的最小值,即可得出结论.
,设M在平面A1B1C1D1中的射影为O,则O为A1B1的中点,ON的最小值,即可得出结论.
【解答】解:由题意,当长方体ABCD﹣A1B1C1D1的体积最大时,长方体ABCD﹣A1B1C1D1为棱长为4的正方体.
N的轨迹是平面A1B1C1D1中,以C1为圆心,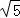 为半径的圆的
为半径的圆的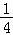 ,
,
设M在平面A1B1C1D1中的射影为O,则O为A1B1的中点,ON的最小值为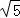 ,
,
∴线段MN的最小值是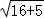 =
= ,
,
故选C.
【点评】本题考查长方体的结构特征,考查学生分析解决问题的能力,属于中档题.
已知双曲线 ,双曲线
,双曲线 的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若
的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若 ,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是( )
,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是( )
A.32 B.16 C.8 D.4
知识点:2.双曲线
B
【考点】双曲线的简单性质.
【分析】求得双曲线C1的离心率,求得双曲线C2一条渐近线方程为y=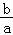 x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.
x,运用点到直线的距离公式,结合勾股定理和三角形的面积公式,化简整理解方程可得a=8,进而得到双曲线的实轴长.
【解答】解:双曲线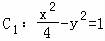 的离心率为
的离心率为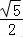 ,
,
设F2(c,0),双曲线C2一条渐近线方程为y=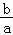 x,
x,
可得|F2M|= =b,
=b,
即有|OM|=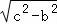 =a,
=a,
由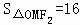 ,可得
,可得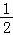 ab=16,
ab=16,
即ab=32,又a2+b2=c2,且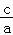 =
=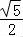 ,
,
解得a=8,b=4,c=4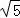 ,
,
即有双曲线的实轴长为16.
故选:B.
【点评】本题考查双曲线的方程和性质,注意运用点到直线的距离公式和离心率公式,考查化简整理的运算能力,属于中档题.
已知函数f(x)= ,x≠0,e为自然对数的底数,关于x的方程
,x≠0,e为自然对数的底数,关于x的方程 +
+ ﹣λ=0有四个相异实根,则实数λ的取值范围是( )
﹣λ=0有四个相异实根,则实数λ的取值范围是( )
A.(0, ) B.(2
) B.(2 ,+∞) C.(e+
,+∞) C.(e+ ,+∞) D.(
,+∞) D.( +
+ ,+∞)
,+∞)
知识点:13.函数与方程
C
【考点】根的存在性及根的个数判断.
【分析】求导数,确定函数的单调性,可得x=2时,函数取得极大值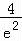 ,关于x的方程
,关于x的方程 +
+ ﹣λ=0有四个相异实根,则t+
﹣λ=0有四个相异实根,则t+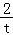 ﹣λ=0的一根在(0,
﹣λ=0的一根在(0,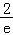 ),另一根在(
),另一根在(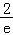 ,+∞)之间,即可得出结论.
,+∞)之间,即可得出结论.
【解答】解:由题意,f′(x)=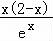 ,
,
∴x<0或x>2时,f′(x)<0,函数单调递减,0<x<2时,f′(x)>0,函数单调递增,
∴x=2时,函数取得极大值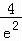 ,
,
关于x的方程 +
+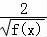 ﹣λ=0有四个相异实根,则t+
﹣λ=0有四个相异实根,则t+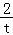 ﹣λ=0的一根在(0,
﹣λ=0的一根在(0, ),另一根在(
),另一根在( ,+∞)之间,
,+∞)之间,
∴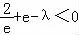 ,∴λ>e+
,∴λ>e+ ,
,
故选:C.
【点评】本题考查函数的单调性,考查方程根问题,考查学生分析解决问题的能力,属于中档题.
直线m经过抛物线C:y2=4x的焦点F,与C交于A,B两点,且|AF|+|BF|=10,则线段AB的中点D到y轴的距离为 .
知识点:3.抛物线
4
【考点】抛物线的简单性质.
【分析】根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标的和,求出线段AB的中点到y轴的距离.
【解答】解:由已知点F(1,0),抛物线C的准线l:x=﹣1,
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+1+x2+1=10,
∴x1+x2=8
∴线段AB的中点横坐标为4
∴线段AB的中点到y轴的距离为4.
故答案为4.
【点评】本题考查解决抛物线上的点到焦点的距离问题,解题的关键是利用抛物线的定义将到焦点的距离转化为到准线的距离.
已知a= ,则二项式
,则二项式 的展开式中的常数项为 .
的展开式中的常数项为 .
知识点:6.微积分的基本定理
﹣84
【考点】二项式系数的性质;定积分.
【分析】根据定积分求出a的值,再利用二项式展开式的通项公式求出展开式中的常数项.
【解答】解:a=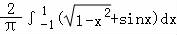
=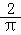
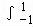
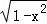 dx+
dx+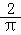
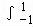 sinxdx
sinxdx
=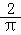 ×
× arcsinx
arcsinx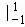 ﹣
﹣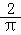 cosx
cosx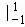
=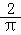 ×
× ×π
×π
=1,
∴二项式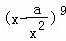 =
=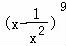 ,
,
其展开式通项公式为:
Tr+1=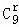 •x9﹣r•
•x9﹣r•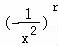
=(﹣1)r•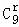 •x9﹣3r,
•x9﹣3r,
令9﹣3r=0,解得r=3,
∴展开式中的常数项为
T4=(﹣1)3•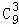 =﹣84.
=﹣84.
故答案为:﹣84.
【点评】本题考查了定积分与二项式展开式的通项公式应用问题,是综合题.
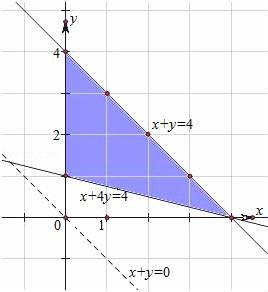
给定区域D: .令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定 条不同的直线.
.令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定 条不同的直线.
知识点:3.二元一次不等式(组)与简单的线性规划
6
【考点】简单线性规划的应用.
【分析】先根据所给的可行域,利用几何意义求最值,z=x+y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最值即可,从而得出点集T中元素的个数,即可得出正确答案.
【解答】解:画出不等式表示的平面区域,如图.
作出目标函数对应的直线,因为直线z=x+y与直线x+y=4平行,故直线z=x+y过直线x+y=4上的整数点:(4,0),(3,1),(2,2),(1,3)或(0,4)时,直线的纵截距最大,z最大;
当直线过(0,1)时,直线的纵截距最小,z最小,从而点集T={(4,0),(3,1),(2,2),(1,3),(0,4),(0,1)},经过这六个点的直线一共有6条.
即T中的点共确定6条不同的直线.
故答案为:6.
【点评】本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.
艾萨克•牛顿(1643年1月4日﹣1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}:满足 ,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设
,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设 ,已知a1=2,xn>2,则{an}的通项公式an= .
,已知a1=2,xn>2,则{an}的通项公式an= .
知识点:4.等比数列及其性质
2n
【考点】数列递推式.
【分析】由已知得到a,b,c的关系,可得f(x)=ax2﹣3ax+2a,求导后代入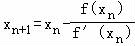 ,整理可得
,整理可得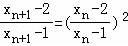 ,两边取对数,可得
,两边取对数,可得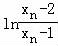 是以2为公比的等比数列,再由等比数列的通项公式求导答案.
是以2为公比的等比数列,再由等比数列的通项公式求导答案.
【解答】解:∵函数f(x)=ax2+bx+c(a>0)有两个零点1,2,
∴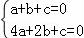 ,解得:
,解得: .
.
∴f(x)=ax2﹣3ax+2a.
则f′(x)=2ax﹣3a.
则 =
=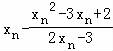 =
= ,
,
∴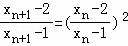 ,
,
则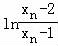 是以2为公比的等比数列,
是以2为公比的等比数列,
∵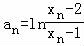 ,且a1=2,
,且a1=2,
∴数列{an}是以2为首项,以2为公比的等比数列,
则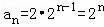 ,
,
故答案为:2n.
【点评】本题考查数列递推式,考查了等比关系的确定,属中档题.
(12分)(2017•江苏模拟)某校园内有一块三角形绿地AEF(如图1),其中AE=20m,AF=10m,∠EAF= ,绿地内种植有一呈扇形AMN的花卉景观,扇形AMN的两边分别落在AE和AF上,圆弧MN与EF相切于点P.
,绿地内种植有一呈扇形AMN的花卉景观,扇形AMN的两边分别落在AE和AF上,圆弧MN与EF相切于点P.
(1)求扇形花卉景观的面积;
(2)学校计划2017年年整治校园环境,为美观起见,设计在原有绿地基础上扩建成平行四边形ABCD(如图2),其中∠BAD= ,并种植两块面积相同的扇形花卉景观,两扇形的边都分别落在平行四边形ABCD的边上,圆弧都与BD相切,若扇形的半径为8m,求平行四边形ABCD绿地占地面积的最小值.
,并种植两块面积相同的扇形花卉景观,两扇形的边都分别落在平行四边形ABCD的边上,圆弧都与BD相切,若扇形的半径为8m,求平行四边形ABCD绿地占地面积的最小值.
知识点:8.三角函数模型的简单应用
【考点】在实际问题中建立三角函数模型.
【分析】(1)△AEF中,由余弦定理可得EF,设扇形花卉景观的半径为r,则由EF•r=AE•AF•sin∠EAF,得到r,即可求扇形花卉景观的面积;
(2)设AB=xm,AD=ym,则BD= m,由平行四边形ABCD的面积得8
m,由平行四边形ABCD的面积得8 =
= xy,求出xy的最小值,即可得出结论.
xy,求出xy的最小值,即可得出结论.
【解答】解:(1)△AEF中,由余弦定理可得EF=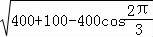 =10
=10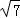 m.
m.
设扇形花卉景观的半径为r,则由EF•r=AE•AF•sin∠EAF,得到r=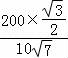 =
=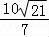 m,
m,
∴扇形花卉景观的面积S= =
= ;
;
(2)设AB=xm,AD=ym,则BD= m,
m,
由平行四边形ABCD的面积得8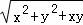 =
=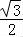 xy,
xy,
∵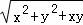 ≥
≥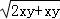 =
= ,
,
∴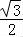 xy≥8
xy≥8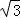
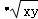 ,即xy≥256,当且仅当x=y=16时,xy的最小值为256,
,即xy≥256,当且仅当x=y=16时,xy的最小值为256,
∴平行四边形ABCD的面积的最小值为128 .
.
【点评】本题考查基本不等式的运用,考查余弦定理的运用,考查学生分析解决问题的能力,难度中等.
如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.

(Ⅰ)求全班人数及分数在[80,100]之间的频率;
(Ⅱ)现从分数在[80,100]之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在[90,100]的份数为X,求X的分布列和数学望期.
知识点:9.离散型随机变量的分布列、均值与方差
【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.
【分析】(I)利用茎叶图的性质、频率的计算公式即可得出.
(II)[80,90)的人数为6人;分数在[90,100)的人数为4人X的取值可能为0,1,2,3.再利用超几何分布列的概率计算公式及其数学期望计算公式即可得出.
【解答】解:(Ⅰ)由茎叶图知分数在[50,60)的人数为4人;[60,70)的人数为8人;[70,80)的人数为10人.
∴总人数为 ….(3分)
….(3分)
∴分数在[80,100)人数为32﹣4﹣8﹣10=10人,∴频率为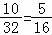 ….
….
(Ⅱ)[80,90)的人数为6人;分数在[90,100)的人数为4人X的取值可能为0,1,2,3.
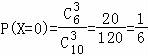 ,
,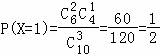 ,
,
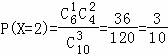 ,
,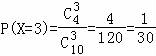 .…(10分)
.…(10分)
∴分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(X)=0+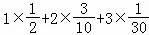 =
= .….(12分)
.….(12分)
【点评】本题考查了超几何分布列的概率计算公式及其数学期望计算公式、茎叶图的性质及其应用,考查了推理能力与计算能力,属于中档题.
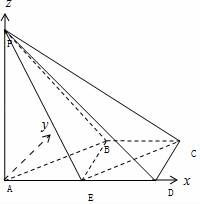
如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.
(Ⅰ)证明:CD⊥平面PAD;
(Ⅱ)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.

知识点:6.直线、平面垂直的判定及其性质
【考点】二面角的平面角及求法;直线与平面垂直的判定.
【分析】(Ⅰ)由已知可得PA⊥CD,再由∠ADC=90°,得CD⊥AD,利用线面垂直的判定可得CD⊥平面PAD;
(Ⅱ)由CD⊥平面PAD,可知∠PDA为二面角P﹣CD﹣A的平面角,从而∠PDA=45°.在平面ABCD内,作Ay⊥AD,以A为原点,分别以AD,AP所在直线为x轴,z轴建立空间直角坐标系A﹣xyz,设BC=1,求出A,P,E,C的坐标,进一步求出平面PCE的一个法向量,由法向量与向量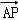 所成角的余弦值的绝对值可得直线PA与平面PCE所成角的正弦值.
所成角的余弦值的绝对值可得直线PA与平面PCE所成角的正弦值.
【解答】(Ⅰ)证明:由已知,PA⊥CD,
又∠ADC=90°,即CD⊥AD,且PA∩AD=A,
∴CD⊥平面PAD;
(Ⅱ)解:∵CD⊥平面PAD,∴∠PDA为二面角P﹣CD﹣A的平面角,从而∠PDA=45°.
如图所示,在平面ABCD内,作Ay⊥AD,以A为原点,分别以AD,AP所在直线为x轴,z轴建立空间直角坐标系A﹣xyz,
设BC=1,则A(0,0,0),P(0,0,2),E(1,0,0),
C(2,1,0),
∴ ,
,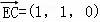 ,
,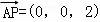 .
.
设平面PCE的一个法向量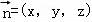 ,
,
则 ,取x=2,则
,取x=2,则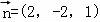 .
.
设直线PA与平面PCE所成角为α,
则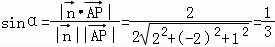 .
.
∴直线PA与平面PCE所成角的正弦值为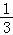 .
.
【点评】本题考查线面垂直的判定,考查利用空间向量求解线面角,是中档题.
已知椭圆C: +
+ =1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若
=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若 且
且
(1)求椭圆C的方程;
(2)已知圆O为原点,圆D:(x﹣3)2+y2=r2(r>0)与椭圆C交于M,N两点,点P为椭圆C上一动点,若直线PM,PN与x轴分别交于点R,S,求证:|OR|•|OS|为常数.

知识点:1.椭圆
【考点】直线与椭圆的位置关系.
【分析】(1)设|BF|=m,推导出(6﹣2m)2+(3m)2=(6﹣m)2,从而m=1,进而AE⊥AF.由此能求出椭圆C的方程.
(2)由条件可知M、N两点关于x轴对称,设M(x1,y1),P(x0,y0),则N(x1,﹣y1),直线PM的方程为 ,令y=0得点R的横坐标
,令y=0得点R的横坐标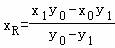 ,同理可得点S的横坐标
,同理可得点S的横坐标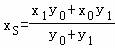 .由此能证明|OR|•|OS|为常数.
.由此能证明|OR|•|OS|为常数.
【解答】解:(1)设|BF|=m,则|AF|=2m,|BE|=6﹣m,|AE|=6﹣2m,|AB|=3m.
则有(6﹣2m)2+(3m)2=(6﹣m)2,解得m=1,…3(分)
∴|AF|=2,|BE|=5,|AE|=4,|AB|=3,
∴|AB|2+|AE|2=|BE|2,∴AE⊥AF.
于是,在Rt△AEF中,|EF|2=|AE|2+|AF|2=42+22=20,
所以|EF|=2 ,所以b2=9﹣(
,所以b2=9﹣( )2=4,
)2=4,
椭圆C的方程为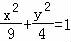 .…6(分)
.…6(分)
证明:(2)由条件可知M、N两点关于x轴对称,
设M(x1,y1),P(x0,y0),则N(x1,﹣y1),
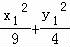 =1,
=1, ,
,
所以 ,
, .
.
直线PM的方程为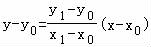 ,…9(分)
,…9(分)
令y=0得点R的横坐标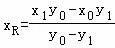 ,
,
同理可得点S的横坐标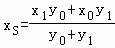 .
.
于是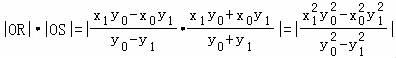
=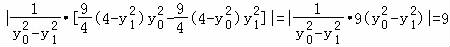 ,
,
所以,|OR|•|OS|为常数9.…12(分)
【点评】本题考查椭圆方程的求法,考查两线段乘积为定值的证明,是中档题,解题时要认真审题,注意椭圆、韦达定理、直线性质的合理运用.
已知函数g(x)=x2+ln(x+a),其中a为常数.
(1)讨论函数g(x)的单调性;
(2)若g(x)存在两个极值点x1,x2,求证:无论实数a取什么值都有 .
.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;利用导数研究函数的极值.
【分析】(1)利用求导法则求出函数g(x)的导函数,把导函数解析式通分化简,分4a2﹣8≤0,或4a2﹣8>0两种情况讨论函数的单调性;
(2)当a>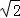 时,函数g(x)在(
时,函数g(x)在(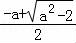 ,+∞)或(﹣a,
,+∞)或(﹣a,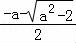 )上单调递增,在(
)上单调递增,在(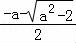 ,
,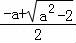 )上单调递减;
)上单调递减;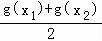 =
=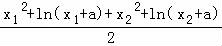 =
=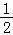 a2﹣
a2﹣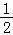 ﹣
﹣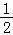 ln2,g(
ln2,g(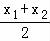 )=g(﹣
)=g(﹣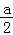 )=
)= +ln
+ln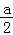 ;令f(a)=
;令f(a)= ﹣lna+
﹣lna+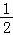 ln2﹣
ln2﹣ ,从而得证.
,从而得证.
【解答】解:(1)∵g(x)=x2+ln(x+a),
∴函数的定义域为(﹣a,+∞)
∴g′(x)=2x+ ,
,
令2x+ >0,
>0,
2x2+2ax+1>0,
当4a2﹣8≤0时,即﹣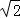 ≤a≤
≤a≤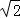 时,g′(x)≥0,即函数g(x)在(﹣a,+∞)单调递增,
时,g′(x)≥0,即函数g(x)在(﹣a,+∞)单调递增,
当4a2﹣8>0时,即a>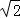 ,或a<﹣
,或a<﹣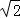 时,
时,
令g′(x)=0,解得x=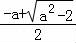 ,或x=
,或x=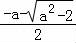 ,
,
①若a> ,
,
当g′(x)>0时,即x>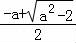 ,或﹣a<x<
,或﹣a<x<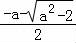 ,函数g(x)单调递增,
,函数g(x)单调递增,
当g′(x)<0时,即 <x<
<x<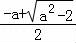 ,函数g(x)单调递减,
,函数g(x)单调递减,
②若a<﹣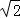 ,g′(x)>0,即函数g(x)在(﹣a,+∞)单调递增,
,g′(x)>0,即函数g(x)在(﹣a,+∞)单调递增,
综上所述:当a≤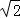 时,即函数g(x)在(﹣a,+∞)单调递增,
时,即函数g(x)在(﹣a,+∞)单调递增,
当a>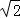 时,函数g(x)在(
时,函数g(x)在(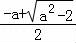 ,+∞)或(﹣a,
,+∞)或(﹣a, )上单调递增,
)上单调递增,
在( ,
,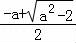 )上单调递减,
)上单调递减,
(2)由(1)可知,当a>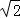 时,函数g(x)在(
时,函数g(x)在(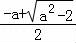 ,+∞)或(﹣a,
,+∞)或(﹣a, )上单调递增,
)上单调递增,
在(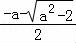 ,
,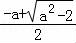 )上单调递减,
)上单调递减,
x1+x2=﹣a;x1•x2=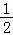 ,
,
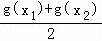 =
=
=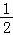 a2﹣
a2﹣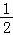 ﹣
﹣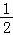 ln2,
ln2,
g(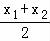 )=g(﹣
)=g(﹣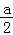 )=
)= +ln
+ln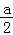 ;
;
故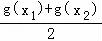 ﹣g(
﹣g(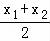 )
)
=( a2﹣
a2﹣ ﹣
﹣ ln2)﹣(
ln2)﹣( +ln
+ln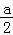 )
)
= ﹣lna+
﹣lna+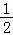 ln2﹣
ln2﹣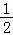 ;
;
令f(a)= ﹣lna+
﹣lna+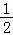 ln2﹣
ln2﹣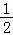 ,
,
则f′(a)=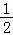 a﹣
a﹣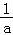 =
=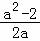 ,
,
∵a>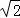 ,∴
,∴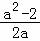 >0;
>0;
∴f(a)= ﹣lna+
﹣lna+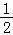 ln2﹣
ln2﹣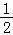 在(
在(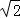 ,+∞)上增函数,
,+∞)上增函数,
且f(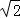 )=0,
)=0,
故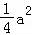 ﹣lna+
﹣lna+ ln2﹣
ln2﹣ >0,
>0,
故无论实数a取什么值都有 .
.
【点评】本题考查了导数的综合应用,同时考查了恒成立问题,属于难题.
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位,已知圆C的参数方程为 (θ为参数),直线l的极坐标方程为ρ=
(θ为参数),直线l的极坐标方程为ρ= ,点P在l上.
,点P在l上.
(1)过P向圆C引切线,切点为F,求|PF|的最小值;
(2)射线OP交圆C于R,点Q在OP上,且满足|OP|2=|OQ|•|OR|,求Q点轨迹的极坐标方程.
知识点:2.坐标系与参数方程
【考点】简单曲线的极坐标方程;参数方程化成普通方程.
【分析】(1)由同角的平方关系可得圆C的普通方程,由y=ρsinθ,x=ρcosθ,可得直线的普通方程,由勾股定理和点到直线的距离公式,可得切线长的最小值;
(2)设P,Q,R的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),代入圆C的极坐标方程和直线的极坐标方程,由同角公式和二倍角的正弦公式,计算即可得到所求轨迹方程.
【解答】解:(1)圆C的参数方程为 (θ为参数),
(θ为参数),
可得圆C的直角坐标方程为x2+y2=4,
直线l的极坐标方程为ρ=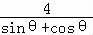 ,
,
即有ρsinθ+ρcosθ=4,
即直线l的直角坐标方程为x+y﹣4=0.
由|PO|2=|PF|2+|OF|2,
由P到圆心O(0,0)的距离d最小时,
|PF|取得最小值.
由点到直线的距离公式可得dmin=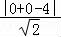 =2
=2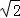 ,
,
可得|PF|最小值为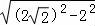 =2;
=2;
(2)设P,Q,R的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),
由ρ1=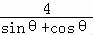 ,ρ2=2,
,ρ2=2,
又|OP|2=|OQ|•|OR|,可得
ρ12=ρρ2,
即有ρ= =
=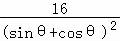 ×
× =
=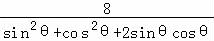
=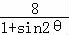 .
.
即Q点轨迹的极坐标方程为ρ=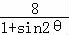 .
.
【点评】本题考查参数方程、极坐标方程和普通方程的互化,考查切线长的最值的求法,注意运用勾股定理和点到直线的距离公式,考查轨迹的极坐标方程的求法,注意运用代入法,考查化简整理的运算能力,属于中档题.
已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]⊆M,求实数a的取值范围.
知识点:3.不等式选讲
【考点】绝对值不等式的解法.
【分析】(1)将x=a﹣3代入不等式,解关于a的不等式即可;(2)得到|x+a|<3恒成立,即﹣3﹣x<a<3﹣x,当x∈[﹣1,1]时恒成立,求出a的范围即可.
【解答】解:(1)依题意有:|2a﹣3|<|a|﹣(a﹣3),
若a≥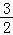 ,则2a﹣3<3,∴
,则2a﹣3<3,∴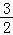 ≤a<3,
≤a<3,
若0≤a<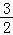 ,则3﹣2a<3,∴0<a<
,则3﹣2a<3,∴0<a<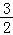 ,
,
若a≤0,则3﹣2a<﹣a﹣(a﹣3),无解,
综上所述,a的取值范围为(0,3);
(2)由题意可知,当x∈[﹣1,1]时,f(x)<g(x)恒成立,
∴|x+a|<3恒成立,
即﹣3﹣x<a<3﹣x,当x∈[﹣1,1]时恒成立,
∴﹣2<a<2.
【点评】本题考查了绝对值不等式问题,考查绝对值的性质,是一道中档题.