已知集合A={0,m,m2﹣3m+2},且2∈A,则实数m为( )
A.2 B.3 C.0或3 D.0,2,3均可
知识点:1.集合的含义与表示
B
【考点】元素与集合关系的判断.
【分析】根据元素2∈A,得到m=2或m2﹣3m+2=2,解方程即可.
【解答】解:∵A={0,m,m2﹣3m+2},且2∈A,
∴m=2或m2﹣3m+2=2,
解得m=2或m=0或m=3.
当m=0时,集合A={0,0,2}不成立.
当m=2时,集合A={0,0,2}不成立.
当m=3时,集合A={0,3,2}成立.
故m=3.
故选:B.
已知集合A={0,1,2},B={1,m}.若A∩B=B,则实数m的值是( )
A.0 B.0或2 C.2 D.0或1或2
知识点:3.集合的基本运算
B
【考点】交集及其运算.
【分析】由A∩B=B,得B⊆A,然后利用子集的概念求得m的值.
【解答】解:∵A∩B=B,∴B⊆A.
当m=0时,B={1,0},满足B⊆A.
当m=2时,B={1,2},满足B⊆A.
∴m=0或m=2.
∴实数m的值为0或2.
故选:B.
函数y=ax+2(a>0且a≠1)图象一定过点( )
A.(0,1) B.(0,3) C.(1,0) D.(3,0)
知识点:8.指数函数及其性质
B
【考点】指数函数的单调性与特殊点.
【分析】由于函数y=ax (a>0且a≠1)图象一定过点(0,1),可得函数y=ax+2图象一定过点(0,3),由此得到答案.
【解答】解:由于函数y=ax (a>0且a≠1)图象一定过点(0,1),故函数y=ax+2(a>0且a≠1)图象一定过点(0,3),
故选B.
下列各组函数中的两个函数是相等函数的是( )
A.f(x)=(x﹣1)0与g(x)=1 B.f(x)=|x|与g(x)=
C.f(x)=x与g(x)=( )2 D.f(x)=
)2 D.f(x)= •
• 与g(x)=
与g(x)=
知识点:1.函数的概念及其表示
B
【考点】判断两个函数是否为同一函数.
【分析】分别判断两个函数定义域和对应法则是否一致即可.
【解答】解:A.函数f(x)=(x﹣1)0=1的定义域{x|x≠1},两个函数的定义域不相同,不是相等函数.
B.g(x)=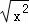 =|x|,两个函数的对应法则和定义域相同,是相等函数.
=|x|,两个函数的对应法则和定义域相同,是相等函数.
C.函数g(x)=( )2=x,函数f(x)的定义域为[0,+∞),两个函数的定义域不相同,不是相等函数.
)2=x,函数f(x)的定义域为[0,+∞),两个函数的定义域不相同,不是相等函数.
D.由 ,解得x≥1,即函数f(x)的定义域为{x|x≥1},
,解得x≥1,即函数f(x)的定义域为{x|x≥1},
由x2﹣1≥0,解得x≥1或x≤﹣1,即g(x)的定义域为{x|x≥1或x≤﹣1},两个函数的定义域不相同,不是相等函数.
故选:B.
集合A={1,x,y},B={1,x2,2y},若A=B,则实数x的取值集合为( )
A.{ } B.{
} B.{ ,﹣
,﹣ } C.{0,
} C.{0, } D.{0,
} D.{0, ,﹣
,﹣ }
}
知识点:2.集合间的基本关系
A
【考点】集合的相等.
【分析】根据集合的相等,得到关于x,y的方程组,解出即可.
【解答】解:集合A={1,x,y},
B={1,x2,2y},
若A=B,则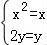 ,解得;x=1或0,y=0,显然不成立,
,解得;x=1或0,y=0,显然不成立,
或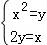 ,解得:x=
,解得:x=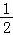 ,
,
故实数x的取值集合为{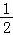 },
},
故选:A.
已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )

A. B.
B. C.
C. D.
D.
知识点:15.函数的图像
A
【考点】指数函数的图象变换;函数的零点与方程根的关系.
【分析】根据题意,易得(x﹣a)(x﹣b)=0的两根为a、b,又由函数零点与方程的根的关系,可得f(x)=(x﹣a)(x﹣b)的零点就是a、b,观察f(x)=(x﹣a)(x﹣b)的图象,可得其与x轴的两个交点分别在区间(﹣∞,﹣1)与(0,1)上,又由a>b,可得b<﹣1,0<a<1;根据函数图象变化的规律可得g(x)=aX+b的单调性即与y轴交点的位置,分析选项可得答案.
【解答】解:由二次方程的解法易得(x﹣a)(x﹣b)=0的两根为a、b;
根据函数零点与方程的根的关系,可得f(x)=(x﹣a)(x﹣b)的零点就是a、b,即函数图象与x轴交点的横坐标;
观察f(x)=(x﹣a)(x﹣b)的图象,可得其与x轴的两个交点分别在区间(﹣∞,﹣1)与(0,1)上,
又由a>b,可得b<﹣1,0<a<1;
在函数g(x)=ax+b可得,由0<a<1可得其是减函数,
又由b<﹣1可得其与y轴交点的坐标在x轴的下方;
分析选项可得A符合这两点,BCD均不满足;
故选A.
已知定义在R上的减函数f(x)满足f(x)+f(﹣x)=0,则不等式f(1﹣x)<0的解集为( )
A.(﹣∞,0) B.(0,+∞) C.(﹣∞,1) D.(1,+∞)
知识点:3.单调性与最大(小)值
C
【考点】奇偶性与单调性的综合.
【分析】由y=f(x)的奇偶性、单调性可得f(x)的图象的对称性及单调性,由此可把不等式化为具体不等式求解.
【解答】解:∵f(x)+f(﹣x)=0,
∴y=f(x)是奇函数,f(0)=0,
∵y=f(x)是减函数,
∴f(1﹣x)<0,即f(1﹣x)<f(0),
由f(x)递减,得1﹣x>0,解得x<1,
∴f(1﹣x)<0的解集为(﹣∞,1),
故选:C.
函数y= 的值域是( )
的值域是( )
A.R B.[ ,+∞) C.(2,+∞) D.(0,+∞)
,+∞) C.(2,+∞) D.(0,+∞)
知识点:8.指数函数及其性质
B
【考点】复合函数的单调性.
【分析】令t=﹣x2+2x,则y=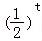 ,再根据t≤1以及指数函数的单调性求得y的值域.
,再根据t≤1以及指数函数的单调性求得y的值域.
【解答】解:令t=﹣x2+2x=﹣(x﹣1)2+1,则y=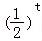 .
.
由于t≤1,∴y≥ =
=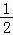 ,
,
故选:B.
设函数f(x)= 如果f(x0)>1,则x0的取值范围是( )
如果f(x0)>1,则x0的取值范围是( )
A.(﹣1,1) B.(﹣1,0)∪(1,+∞) C.(﹣∞,﹣1)∪(1,+∞) D.(﹣∞,﹣1)∪(0,1)
知识点:12.绝对值函数与分段函数及其他函数
C
【考点】分段函数的应用.
【分析】根据分段函数的表达式,进行求解即可.
【解答】解:若x0>0,由f(x0)>1得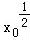 =
=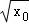 >1得x0>1,
>1得x0>1,
若x0≤0,由f(x0)>1得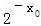 ﹣1>1得
﹣1>1得 >2,
>2,
即﹣x0>1,则x0<﹣1,
综上x0>1或x0<﹣1,
故选:C
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )

A. B.
B. C.
C. D.
D.
知识点:1.函数的概念及其表示
C
【考点】函数的图象.
【分析】直接利用图形的形状,结合图象,判断不满足的图形即可.
【解答】解:由函数的图象可知,几何体具有对称性,
选项A、B、D,l在移动过程中扫过平面图形的面积为y,在中线位置前,都是先慢后快,然后相反.
选项C,后面是直线增加,不满足题意;
故选:C、
若函数 f(x)=ae﹣x﹣ex为奇函数,则f(x﹣1)<e﹣ 的解集为( )
的解集为( )
A.(﹣∞,0) B.(﹣∞,2) C.(2,+∞) D.(0,+∞)
知识点:5.奇偶性与周期性
D
【考点】函数奇偶性的性质.
【分析】根据f(x)为R上的奇函数便有f(0)=0,从而可求得a=1,这便得到f(x)=e﹣x﹣ex,求导数可得出f′(x)<0,从而得出f(x)在R上单调递减,而f(﹣1)=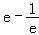 ,从而由原不等式得到f(x﹣1)<f(﹣1),从而有x﹣1>﹣1,这样便可得出原不等式的解集.
,从而由原不等式得到f(x﹣1)<f(﹣1),从而有x﹣1>﹣1,这样便可得出原不等式的解集.
【解答】解:f(x)在R上为奇函数;
∴f(0)=0;
即a﹣1=0;
∴a=1;
∴f(x)=e﹣x﹣ex,f'(x)=﹣e﹣x﹣ex<0;
∴f(x)在R上单调递减;
∴由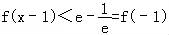 得:x﹣1>﹣1;
得:x﹣1>﹣1;
即x>0;
∴原不等式的解集为(0,+∞).
故选D.
已知f(x)=2x+2﹣x,f(m)=3,且m>0,若a=f(2m),b=2f(m),c=f(m+2),则a,b,c的大小关系为( )
A.c<b<a B.a<c<b C.a<b<c D.b<a<c
知识点:8.指数函数及其性质
D
【考点】函数的值.
【分析】可得f(m)=2m+2﹣m=3,2m>2,从而化简比较大小.
【解答】解:∵f(m)=2m+2﹣m=3,m>0,
∴2m=3﹣2﹣m>2,
∴b=2f(m)=2×3=6,
a=f(2m)=22m+2﹣2m=(2m+2﹣m)2﹣2=7,
c=f(m+2)=2m+2+2﹣m﹣2=4•2m+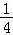 2﹣m>8,
2﹣m>8,
∴b<a<c;
故选D.
已知| |=12,|
|=12,| |=9,
|=9, •
• =﹣54
=﹣54 ,则
,则 与
与 的夹角为 .
的夹角为 .
知识点:4.平面向量的数量积(夹角、模)
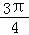
【考点】平面向量数量积的运算.
【分析】运用向量的数量积的定义,结合向量夹角的范围和特殊角的三角函数值,即可得到.
【解答】解:由|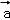 |=12,|
|=12,|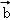 |=9,
|=9,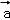 •
•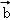 =﹣54
=﹣54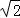 ,
,
可得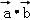 =12×9cos<
=12×9cos<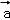 ,
,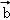 >=﹣54
>=﹣54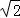 ,
,
即cos<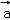 ,
,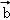 >=﹣
>=﹣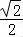 ,
,
由0≤<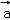 ,
,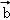 >≤π,
>≤π,
则有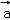 与
与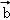 的夹角为
的夹角为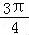 .
.
故答案为: .
.
已知sin2α=﹣sinα,则tanα= .
知识点:5.三角函数的求值、化简与证明
± 或0
或0
【考点】二倍角的正弦.
【分析】sin2α=﹣sinα,可得sinα(2cosα+1)=0,解得:sinα=0,cosα=﹣ ,进而得出.
,进而得出.
【解答】解:∵sin2α=﹣sinα,
∴sinα(2cosα+1)=0,
解得:sinα=0,或cosα=﹣ ,
,
若sinα=0,则tanα=0,
若cosα=﹣ ,则sinα=
,则sinα= ,∴tanα=±
,∴tanα=± .
.
故答案为:±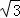 或0.
或0.
设a= ,b=
,b= ,c=
,c= cos81°+
cos81°+ sin99°,将a,b,c用“<”号连接起来 .
sin99°,将a,b,c用“<”号连接起来 .
知识点:5.三角函数的求值、化简与证明
b<c<a
【考点】三角函数的化简求值.
【分析】利用二倍角公式化简a,b,再由两角和的正弦化简c,然后结合正弦函数的单调性得答案.
【解答】解:∵a= =sin140°=sin40°,
=sin140°=sin40°,
b=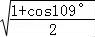 =
= =sin35.5°,
=sin35.5°,
c= cos81°+
cos81°+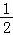 sin99°=
sin99°=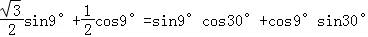 =sin39°,
=sin39°,
且y=sinx在[0°,90°]内为增函数,
∴b<c<a.
故答案为:b<c<a.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=3,则 = .
= .

知识点:4.平面向量的数量积(夹角、模)
18
【考点】平面向量数量积的运算.
【分析】设AC与BD交于O,则AC=2AO,在RtAPO中,由三角函数可得AO与AP的关系,代入向量的数量积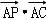 =|
=|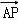 ||
||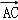 |cos∠PAO可求
|cos∠PAO可求
【解答】解:设AC与BD交于点O,则AC=2AO
∵AP⊥BD,AP=3,
在Rt△APO中,AOcos∠OAP=AP=3
∴|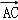 |cos∠OAP=2|
|cos∠OAP=2|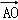 |×cos∠OAP=2|
|×cos∠OAP=2|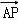 |=6,
|=6,
由向量的数量积的定义可知,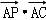 =|
=|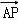 ||
||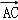 |cos∠PAO=3×6=18
|cos∠PAO=3×6=18
故答案为:18
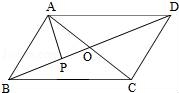
已知 .
.
(Ⅰ)求tanα的值;
(Ⅱ)求 的值.
的值.
知识点:5.三角函数的求值、化简与证明
【考点】同角三角函数基本关系的运用.
【分析】(Ⅰ)利用和角的正切公式,化简可求tanα的值;
(Ⅱ)利用二倍角公式,再弦化切,即可求得结论.
【解答】解:(Ⅰ)因为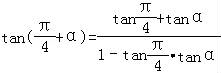 =
= ,所以
,所以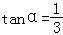 ;
;
(Ⅱ)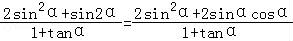 =
=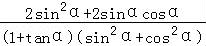 =
=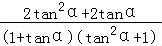 =
=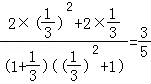 .
.
在锐角△ABC中,a,b,c分别为内角A,B,C,所对的边,且满足 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若a+c=5,且a>c,b= ,求
,求 的值.
的值.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;平面向量数量积的运算;正弦定理.
【分析】(Ⅰ)利用正弦定理化简已知的等式,根据sinA不为0,可得出sinB的值,由B为锐角,利用特殊角的三角函数值即可求出B的度数;
(Ⅱ)由b及cosB的值,利用余弦定理列出关于a与c的关系式,利用完全平方公式变形后,将a+c的值代入,求出ac的值,将a+c=5与ac=6联立,并根据a大于c,求出a与c的值,再由a,b及c的值,利用余弦定理求出cosA的值,然后将所求的式子利用平面向量的数量积运算法则化简后,将b,c及cosA的值代入即可求出值.
【解答】解:(Ⅰ)∵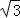 a﹣2bsinA=0,
a﹣2bsinA=0,
∴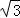 sinA﹣2sinBsinA=0,…
sinA﹣2sinBsinA=0,…
∵sinA≠0,∴sinB=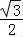 ,…
,…
又B为锐角,则B=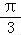 ;…
;…
(Ⅱ)由(Ⅰ)可知B=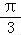 ,又b=
,又b=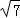 ,
,
根据余弦定理,得b2=7=a2+c2﹣2accos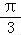 ,…
,…
整理得:(a+c)2﹣3ac=7,
∵a+c=5,∴ac=6,
又a>c,可得a=3,c=2,…
∴cosA= =
=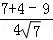 =
=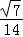 ,…
,…
则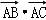 =|
=| |•|
|•|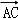 |cosA=cbcosA=2×
|cosA=cbcosA=2×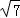 ×
×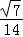 =1.…
=1.…
已知数列{an}的前n项和为Sn,若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn= ,数列{cn}的前n项和为Tn.
,数列{cn}的前n项和为Tn.
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围.
知识点:6.数列的求和
【考点】数列递推式;数列的求和.
【分析】(1)充分利用已知4Sn=(2n﹣1)an+1+1,将式子中n换成n﹣1,然后相减得到an与an+1的关系,利用累乘法得到数列的通项,
(2)①利用裂项求和,即可求出Tn,
②根据函数的思想求出 ≥
≥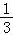 ,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
【解答】解:(1)∵4Sn=(2n﹣1)an+1+1,
∴4Sn﹣1=(2n﹣3)an+1,n≥2
∴4an=(2n﹣1)an+1﹣(2n﹣3)an,
整理得(2n+1)an=(2n﹣1)an+1,
即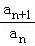 =
= ,
,
∴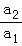 =3,
=3,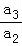 =
=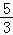 ,…,
,…,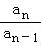 =
=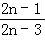
以上各式相乘得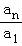 =2n﹣1,又a1=1,
=2n﹣1,又a1=1,
所以an=2n﹣1,
(2)①∵cn=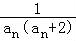 =
= =
= (
(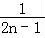 ﹣
﹣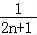 ),
),
∴Tn=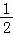 (1﹣
(1﹣ +
+ ﹣
﹣ +…+
+…+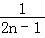 ﹣
﹣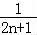 )=
)=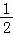 (1﹣
(1﹣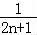 )=
)=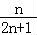 ,
,
②由①可知Tn=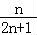 ,
,
∴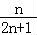 ≥
≥ ,
,
∵kx2﹣6kx+k+7+3Tn>0恒成立,
∴kx2﹣6kx+k+8>0恒成立,
当k=0时,8>0恒成立,
当k≠0时,则得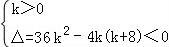 ,解得0<k<1,
,解得0<k<1,
综上所述实数k的取值范围为[0,1).
设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 =
= ,求D点的坐标;
,求D点的坐标;
(2)设向量 =
= ,
, =
= ,若k
,若k ﹣
﹣ 与
与 +3
+3 平行,求实数k的值.
平行,求实数k的值.
知识点:3.平面向量的基本定理及其坐标表示
【考点】平面向量共线(平行)的坐标表示;相等向量与相反向量.
【分析】(1)利用向量相等即可得出;
(2)利用向量共线定理即可得出.
【解答】解:(1)设D(x,y).∵ ,
,
∴(2,﹣2)﹣(1,3)=(x,y)﹣(4,1),
化为(1,﹣5)=(x﹣4,y﹣1),
∴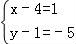 ,解得
,解得 ,
,
∴D(5,﹣4).
(2)∵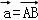 =(1,﹣5),
=(1,﹣5),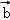 =
=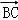 =(4,1)﹣(2,﹣2)=(2,3).
=(4,1)﹣(2,﹣2)=(2,3).
∴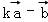 =k(1,﹣5)﹣(2,3)=(k﹣2,﹣5k﹣3),
=k(1,﹣5)﹣(2,3)=(k﹣2,﹣5k﹣3), =(1,﹣5)+3(2,3)=(7,4).
=(1,﹣5)+3(2,3)=(7,4).
∵k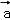 ﹣
﹣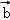 与
与 +3
+3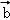 平行,
平行,
∴7(﹣5k﹣3)﹣4(k﹣2)=0,解得k=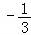 .
.
∴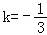 .
.
已知函数f(x)=Asin(x+ ),x∈R,且f(
),x∈R,且f( )=
)= .
.
(1)求A的值;
(2)若f(θ)+f(﹣θ)= ,θ∈(0,
,θ∈(0, ),求f(
),求f( ﹣θ).
﹣θ).
知识点:7.函数y=Asin(wx+@)+B
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;两角和与差的正弦函数.
【分析】(1)由函数f(x)的解析式以及f( )=
)=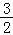 ,求得A的值.
,求得A的值.
(2)由(1)可得 f(x)= sin(x+
sin(x+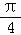 ),根据f(θ)+f(﹣θ)=
),根据f(θ)+f(﹣θ)=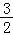 ,求得cosθ 的值,再由 θ∈(0,
,求得cosθ 的值,再由 θ∈(0,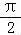 ),求得sinθ 的值,从而求得f(
),求得sinθ 的值,从而求得f(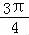 ﹣θ) 的值.
﹣θ) 的值.
【解答】解:(1)∵函数f(x)=Asin(x+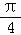 ),x∈R,且f(
),x∈R,且f(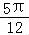 )=
)=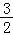 .
.
∴Asin(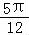 +
+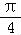 )=Asin
)=Asin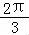 =A•
=A•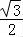 =
=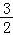 ,
,
∴A=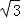 .
.
(2)由(1)可得 f(x)=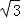 sin(x+
sin(x+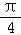 ),
),
∴f(θ)+f(﹣θ)= sin(θ+
sin(θ+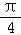 )+
)+ sin(﹣θ+
sin(﹣θ+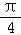 )=2
)=2 sin
sin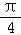 cosθ=
cosθ=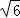 cosθ=
cosθ=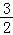 ,
,
∴cosθ= ,再由 θ∈(0,
,再由 θ∈(0,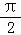 ),可得sinθ=
),可得sinθ=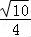 .
.
∴f(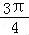 ﹣θ)=
﹣θ)= sin(
sin(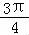 ﹣θ+
﹣θ+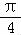 )=
)=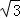 sin(π﹣θ)=
sin(π﹣θ)=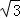 sinθ=
sinθ=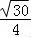 .
.
在等比数列{an}中,a1=2,a3,a2+a4,a5成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+ +…+
+…+ =an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
=an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
知识点:4.等比数列及其性质
【考点】数列的求和.
【分析】(1)根据等比数列和等差数列的通项公式建立方程关系进行求解即可.
(2)利用方程法求出数列{bn}的通项公式,利用错位相减法求出{bn}的前n项和公式,解不等式即可.
【解答】解:(1)∵等比数列{an}中,a1=2,a3,a2+a4,a5成等差数列.
∴2(a2+a4)=a3+a5,
即2(a2+a4)=q(a2+a4),
∴q=2,
则an=a1qn﹣1=2×2n﹣1=2n,
即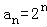 ;
;
(2)∵数列{bn}满足b1+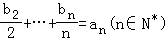 ,
,
∴b1+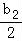 +…+
+…+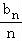 +
+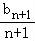 =an+1,
=an+1,
两式相减得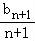 =an+1﹣an=2n+1﹣2n=2n,
=an+1﹣an=2n+1﹣2n=2n,
则bn+1=(n+1)•2n,即bn=n•2n﹣1,n≥2,
当n=1时,b1=a1=2,不满足bn=n•2n﹣1,n≥2.
即bn=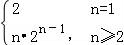 .
.
当n=1时,不等式等价为S1﹣a1+6=6≥0成立,
当n≥2时,
Sn=2+2•21+3•22+4•23+…+n•2n﹣1,①
则2Sn=4+2•22+3•23+4•24+…+n•2n,②
②﹣①,得Sn=2+2•21﹣22﹣23﹣24﹣…﹣2n﹣1+n•2n=6﹣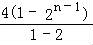 +n•2n=6+n•2n=6+4﹣2n+1+n•2n=10+(n﹣2)•2n,
+n•2n=6+n•2n=6+4﹣2n+1+n•2n=10+(n﹣2)•2n,
则当n≥2时,不等式Sn﹣nan+6≥0等价为10+(n﹣2)•2n﹣n•2n+6≥0,
即16﹣2•2n≥0,则2n≤8,得n≤3,
则n的最大值是3.