若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b),则
 的值为( )
的值为( )
A.f′(x0) B.2f′(x0) C.﹣2f′(x0) D.0
知识点:1.变化率与导数
B
【考点】变化的快慢与变化率.
【分析】由题意,根据导数的定义,可知f′(x0)=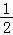
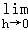
 ,即可得出结论.
,即可得出结论.
【解答】解:由题意,根据导数的定义,可知f′(x0)=
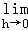
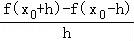 ,
,
∴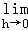
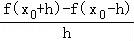 =2f′(x0),
=2f′(x0),
故选B.
一个物体的运动方程为s=1﹣t+t2其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
A.7米/秒 B.6米/秒 C.5米/秒 D.8米/秒
知识点:1.变化率与导数
C
【考点】导数的几何意义.
【分析】求导数,把t=3代入求得导数值即可.
【解答】解:∵s=1﹣t+t2,∴s′=﹣1+2t,
把t=3代入上式可得s′=﹣1+2×3=5
由导数的意义可知物体在3秒末的瞬时速度是5米/秒,
故选C
函数y=x3﹣3x的单调递减区间是( )
A.(﹣∞,0) B.(0,+∞) C.(﹣∞,﹣1),(1,+∞) D.(﹣1,1)
知识点:3.导数在研究函数中的应用
D
【考点】利用导数研究函数的单调性.
【分析】求导,令导数小于零,解此不等式即可求得函数y=x3﹣3x的单调递减区间.
【解答】解:令y′=3x2﹣3<0
解得﹣1<x<1,
∴函数y=x3﹣3x的单调递减区间是(﹣1,1).
故选D.
曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
A.(1,0) B.(2,8) C.(1,0)或(﹣1,﹣4) D.(2,8)或(﹣1,﹣4)
知识点:1.变化率与导数
C
【考点】利用导数研究曲线上某点切线方程.
【分析】利用直线平行的性质,结合导数的几何意义求出切线的斜率,即可求出切点的坐标.
【解答】解:因为直线y=4x﹣1的斜率为4,且切线平行于直线y=4x﹣1,
所以函数在p0处的切线斜率k=4,即f'(x)=4.
因为函数的导数为f'(x)=3x2+1,
由f'(x)=3x2+1=4,解得x=1或﹣1.
当x=1时,f(1)=0,当x=﹣1时,f(﹣1)=﹣4.
所以p0的坐标为(1,0)或(﹣1,﹣4).
故选C.
已知f(x)与g(x)是定义在R上的两个可导函数,若f(x)与g(x)满足f′(x)=g′(x),则( )
A.f(x)=g(x) B.f(x)﹣g(x)为常数函数
C.f(x)=g(x)=0 D.f(x)+g(x)为常数函数
知识点:3.导数在研究函数中的应用
B
【考点】导数的运算.
【分析】根据导数的运算法则构造函数即可得到结论.
【解答】解:设h(x)=f(x)﹣g(x),
则h′(x)=f′(x)﹣g′(x)=0,
即h(x)=f(x)﹣g(x)是常数,
故选:B
函数 的最大值为( )
的最大值为( )
A.e﹣1 B.e C.e2 D.
知识点:3.导数在研究函数中的应用
A
【考点】函数在某点取得极值的条件.
【分析】先找出导数值等于0的点,再确定在此点的左侧及右侧导数值的符号,确定此点是函数的极大值点还是极小值点,
从而求出极值.
【解答】解:令 ,
,
当x>e时,y′<0;
当x<e时,y′>0,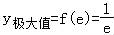 ,
,
在定义域内只有一个极值,
所以 ,
,
故答案选 A.
“可导函数y=f(x)在一点的导数值是0”是“函数y=f(x)在这点取极值”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
A
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据函数极值的定义以及充分条件和必要条件的定义进行判断即可.
【解答】解:函数y=f(x)在一点的导数值是0,则函数y=f(x)在这点不一定取极值,比如函数f(x)=x3,满足f'(0)=0,但x=0不是极值.
若函数y=f(x)在这点取极值,则根据极值的定义可知,y=f(x)在一点的导数值是0成立,
∴“函数y=f(x)在一点的导数值是0”是“函数y=f(x)在这点取极值”必要不充分条件.
故选:A.
不等式x2﹣|x|﹣2<0(x∈R)的解集是( )
A.{x|x<﹣1或x>1} B.{x|x<﹣2或x>2} C.{x|﹣1<x<1} D.{x|﹣2<x<2}
知识点:3.不等式选讲
D
【考点】其他不等式的解法.
【分析】把原不等式中的x2变为|x|2,则不等式变为关于|x|的一元二次不等式,求出解集得到关于x的绝对值不等式,解出绝对值不等式即可得到x的解集.
【解答】解:原不等式化为|x|2﹣|x|﹣2<0
因式分解得(|x|﹣2)(|x|+1)<0
因为|x|+1>0,所以|x|﹣2<0即|x|<2
解得:﹣2<x<2.
故选D.
ab≥0是|a﹣b|=|a|﹣|b|的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
A
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分条件和必要条件的定义,以及绝对值的意义进行判断即可.
【解答】解:当a=1,b=2时,不满足|a﹣b|=|a|﹣|b|,
当“|a﹣b|=|a|﹣|b|”,∴平方得a2﹣2ab+b2=a2﹣2|ab|+b2,
即|ab|=ab,可得ab≥0.
∴即“ab≥0是|a﹣b|=|a|﹣|b|的|”的必要不充分条件.
故选:A.
已知a,b∈R,ab>0,则下列不等式中不正确的是( )
A.|a+b|≥a﹣b B. C.|a+b|<|a|+|b| D.
C.|a+b|<|a|+|b| D.
知识点:3.不等式选讲
C
【考点】不等关系与不等式.
【分析】根据不等式的性质和基本不等式判断即可.
【解答】解:对于A:∵ab>0,当a>0,b>0时,|a+b|=a+b≥a﹣b,当a<0,b<0时,|a+b|=﹣a﹣b≥a﹣b,故A成立,
对于B:当ab>0,∴(a+b)2=a2+b2+2ab≥4ab,故B成立,
对于C:a>0,b>0时,或a<0,b<0,时|a+b|=|a|+|b|,故C不正确,
对于D:ab>0,∴|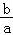 +
+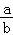 |=
|=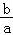 +
+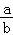 ≥2
≥2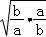 =2,当且仅当a=b时取等号,故D成立
=2,当且仅当a=b时取等号,故D成立
故选:C
对任意实数x,若不等式|x+2|+|x+1|>k恒成立,则实数k的取值范围是( )
A.k>1 B.k=1 C.k≤1 D.k<1
知识点:3.不等式选讲
D
【考点】函数恒成立问题;绝对值不等式.
【分析】若不等式|x+2|+|x+1|>k恒成立,只需 k小于|x+2|+|x+1|的最小值即可.由绝对值的几何意义,求出|x+2|+|x+1|取得最小值1,得k<1
【解答】解:若不等式|x+2|+|x+1|>k恒成立,只需 k小于|x+2|+|x+1|的最小值即可.
由绝对值的几何意义,|x+2|+|x+1|表示在数轴上点x到﹣2,﹣1点的距离之和.当点x在﹣2,﹣1点之间时(包括﹣1,﹣2点),
即﹣2≤x≤﹣1时,|x+2|+|x+1|取得最小值1,∴k<1
故选D
f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)<0,且f(﹣2)=0,则不等式f(x)g(x)<0的解集为( )
A.(﹣2,0)∪(2,+∞) B.(﹣2,0)∪(0,2) C.(﹣∞,﹣2)∪(2,+∞) D.(﹣∞,﹣2)∪(0,2)
知识点:3.导数在研究函数中的应用
A
【考点】利用导数研究函数的单调性;奇偶性与单调性的综合.
【分析】令h(x)=f(x)g(x),依题意可知h(x)=f(x)g(x)为R上的奇函数,在对称区间上有相同的单调性,f(﹣2)=0,从而可求得f(x)g(x)<0的解集.
【解答】解:令h(x)=f(x)g(x),
∵f(x),g(x)分别是定义在R上的奇函数和偶函数,
∴h(x)=f(x)g(x)为R上的奇函数.
又当x<0时,h′(x)=f′(x)g(x)+f(x)g′(x)<0,
∴h(x)=f(x)g(x)在(﹣∞,0)上单调递减,
又h(x)=f(x)g(x)为R上的奇函数,
∴h(x)=f(x)g(x)在(0,+∞)上单调递减,
又f(﹣2)=0,故f(2)=0,
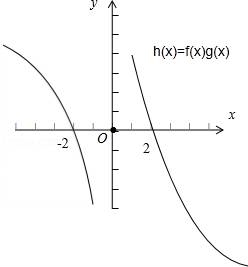
∴当﹣2<x<0,或x>2时,f(x)g(x)<0.
故f(x)g(x)<0的解集为(﹣2,0)∪(2,+∞).
故选A.
函数y=x+2cosx在区间 上的最大值是 .
上的最大值是 .
知识点:3.导数在研究函数中的应用
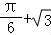
【考点】利用导数求闭区间上函数的最值.
【分析】对函数y=x+2cosx进行求导,研究函数在区间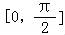 上的极值,本题极大值就是最大值.
上的极值,本题极大值就是最大值.
【解答】解:∵y=x+2cosx,∴y′=1﹣2sinx
令y′=0而x∈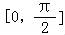 则x=
则x=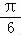 ,
,
当x∈[0,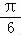 ]时,y′>0.
]时,y′>0.
当x∈[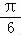 ,
,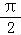 ]时,y′<0.
]时,y′<0.
所以当x= 时取极大值,也是最大值;
时取极大值,也是最大值;
故答案为
已知|2x﹣3|≤1的解集为[m,n],则m+n的值为 .
知识点:2.一元二次不等式及不等式的解法
3
【考点】其他不等式的解法.
【分析】由|2x﹣3|≤1,可得﹣1≤2x﹣3≤1,求得1≤x≤2.再根据|2x﹣3|≤1的解集为[m,n],可得m和n的值,可得 m+n的值
【解答】解:(1)由|2x﹣3|≤1,可得﹣1≤2x﹣3≤1,求得1≤x≤2.
再根据|2x﹣3|≤1的解集为[m,n],可得m=1,n=2,∴m+n=3,
故答案为:3
函数f(x)=x3+x2+mx+1是R上的单调函数,则m的取值范围为 .
知识点:3.导数在研究函数中的应用
[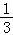 ,+∞)
,+∞)
【考点】利用导数研究函数的单调性.
【分析】对函数进行求导,令导函数大于等于0在R上恒成立即可.
【解答】解:若函数y=x3+x2+mx+1是R上的单调函数,
只需y′=3x2+2x+m≥0恒成立,
即△=4﹣12m≤0,
∴m≥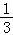 .
.
故m的取值范围为[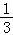 ,+∞).
,+∞).
故答案为:[ ,+∞).
,+∞).
对正整数n,设曲线y=xn(1﹣x)在x=2处的切线与y轴交点的纵坐标为an,则数列 的前n项和的公式是 .
的前n项和的公式是 .
知识点:1.变化率与导数
2n+1﹣2
【考点】利用导数研究曲线上某点切线方程;数列的求和.
【分析】欲求数列 的前n项和,必须求出在点(1,1)处的切线方程,须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率即得直线方程进而得到切线与y轴交点的纵坐标.最后利用等比数列的求和公式计算,从而问题解决.
的前n项和,必须求出在点(1,1)处的切线方程,须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率即得直线方程进而得到切线与y轴交点的纵坐标.最后利用等比数列的求和公式计算,从而问题解决.
【解答】解:y′=nxn﹣1﹣(n+1)xn,
曲线y=xn(1﹣x)在x=2处的切线的斜率为k=n2n﹣1﹣(n+1)2n
切点为(2,﹣2n),
所以切线方程为y+2n=k(x﹣2),
令x=0得an=(n+1)2n,
令bn= .
.
数列 的前n项和为2+22+23+…+2n=2n+1﹣2.
的前n项和为2+22+23+…+2n=2n+1﹣2.
故答案为:2n+1﹣2.
导数计算:
(Ⅰ)y=xlnx;
(Ⅱ) .
.
知识点:2.导数的计算
【考点】导数的运算.
【分析】(Ⅰ)根据题意,由导数的乘法运算法则可得y′=(x)′•lnx+x•(lnx)′=lnx+1,即可得答案;
(Ⅱ)由导数除法的运算法则可得y′=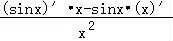 =
=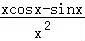 ,即可得答案.
,即可得答案.
【解答】解:(Ⅰ)根据题意,y=xlnx;
其导数y′=(x)′•lnx+x•(lnx)′=lnx+1,
即y'=lnx+1;
(Ⅱ)y= ,
,
其导数y′=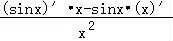 =
=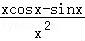 ,
,
即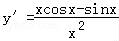 .
.
已知函数f(x)=x3﹣x2+x+2.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求经过点A(1,3)的曲线f(x)的切线方程.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究曲线上某点切线方程.
【分析】(1)求出f(x)的导数,可得切线的斜率和切点,运用点斜式方程可得所求切线的方程;
(2)设切点为(m,n),代入f(x),求得切线的斜率和方程,代入点A(1,3),解m的方程可得m=0或1,即可得到所求切线的方程.
【解答】解:(1)函数f(x)=x3﹣x2+x+2的导数为f′(x)=3x2﹣2x+1,
可得曲线f(x)在点(1,f(1))处的切线斜率为3﹣2+1=2,
切点为(1,3),
即有曲线f(x)在点(1,f(1))处的切线方程为y﹣3=2(x﹣1),
即为2x﹣y+1=0;
(2)设切点为(m,n),可得n=m3﹣m2+m+2,
由f(x)的导数f′(x)=3x2﹣2x+1,
可得切线的斜率为3m2﹣2m+1,
切线的方程为y﹣(m3﹣m2+m+2)=(3m2﹣2m+1)(x﹣m),
由切线经过点(1,3),可得
3﹣(m3﹣m2+m+2)=(3m2﹣2m+1)(1﹣m),
化为m(m﹣1)2=0,解得m=0或1.
则切线的方程为y﹣2=x或y﹣3=2(x﹣1),
即为y=x+2或y=2x+1.
(Ⅰ)求不等式|x+3|﹣|x﹣2|≥3的解集;
(Ⅱ)设a>b>0,求证: >
> .
.
知识点:3.不等式选讲
【考点】不等式的证明;绝对值不等式的解法.
【分析】(Ⅰ)根据绝对值不等式可化为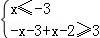 ,或
,或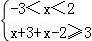 或
或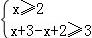 ,解得即可,
,解得即可,
(Ⅱ)法一,利用作差法比较即可,
法二,利用做商法比较即可.
【解答】(Ⅰ)解:原不等式等价于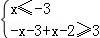 ,或
,或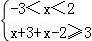 或
或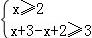 ,
,
解得1≤x<2或x≥2,
故原不等式的解集为{x|x≥1}.
(Ⅱ)证明:法一: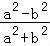 ﹣
﹣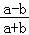 =
=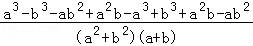 ,
,
=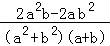 =
= ,
,
因为a>b>0,所以a﹣b>0,ab>0,a2+b2>0,a+b>0.
所以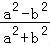 ﹣
﹣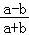 >0,
>0,
所以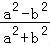 >
>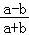
法二:因为a>b>0,所以a+b>0,a﹣b>0.
所以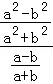 =
=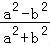 •
•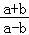 =
=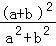 =
=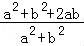 =1+
=1+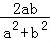 >1.
>1.
所以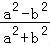 >
>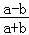
已知函数f(x)=x3+ax2+bx+c在x=﹣ 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)若对x∈[﹣1,2],不等式f(x)<c2恒成立,求c的取值范围.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的极值;函数恒成立问题;利用导数研究函数的单调性.
【分析】(1)求出f′(x),因为函数在x=﹣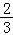 与x=1时都取得极值,所以得到f′(﹣
与x=1时都取得极值,所以得到f′(﹣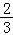 )=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
)=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
(2)根据(1)函数的单调性,由于x∈[﹣1,2]恒成立求出函数的最大值值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可.
【解答】解;(1)f(x)=x3+ax2+bx+c,f'(x)=3x2+2ax+b
由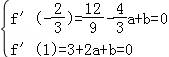 解得,
解得,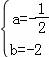
f'(x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
x | (﹣∞,﹣ | ﹣ | (﹣ | 1 | (1,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以函数f(x)的递增区间是(﹣∞,﹣ )和(1,+∞),递减区间是(﹣
)和(1,+∞),递减区间是(﹣ ,1).
,1).
(2)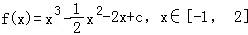 ,
,
当x=﹣ 时,f(x)=
时,f(x)=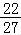 +c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值.
+c为极大值,而f(2)=2+c,所以f(2)=2+c为最大值.
要使f(x)<c2对x∈[﹣1,2]恒成立,须且只需c2>f(2)=2+c.
解得c<﹣1或c>2.
已知函数f(x)=|x﹣ |+|x+
|+|x+ |,M为不等式f(x)<2的解集.
|,M为不等式f(x)<2的解集.
(Ⅰ)求M;
(Ⅱ)证明:当a,b∈M时,|a+b|<|1+ab|.
知识点:3.不等式选讲
【考点】绝对值不等式的解法.
【分析】(I)分当x<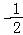 时,当
时,当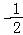 ≤x≤
≤x≤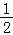 时,当x>
时,当x>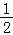 时三种情况,分别求解不等式,综合可得答案;
时三种情况,分别求解不等式,综合可得答案;
(Ⅱ)当a,b∈M时,(a2﹣1)(b2﹣1)>0,即a2b2+1>a2+b2,配方后,可证得结论.
【解答】解:(I)当x<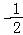 时,不等式f(x)<2可化为:
时,不等式f(x)<2可化为: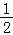 ﹣x﹣x﹣
﹣x﹣x﹣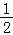 <2,
<2,
解得:x>﹣1,
∴﹣1<x<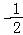 ,
,
当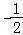 ≤x≤
≤x≤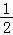 时,不等式f(x)<2可化为:
时,不等式f(x)<2可化为: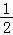 ﹣x+x+
﹣x+x+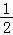 =1<2,
=1<2,
此时不等式恒成立,
∴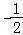 ≤x≤
≤x≤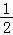 ,
,
当x>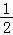 时,不等式f(x)<2可化为:﹣
时,不等式f(x)<2可化为:﹣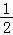 +x+x+
+x+x+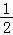 <2,
<2,
解得:x<1,
∴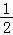 <x<1,
<x<1,
综上可得:M=(﹣1,1);
证明:(Ⅱ)当a,b∈M时,
(a2﹣1)(b2﹣1)>0,
即a2b2+1>a2+b2,
即a2b2+1+2ab>a2+b2+2ab,
即(ab+1)2>(a+b)2,
即|a+b|<|1+ab|.
已知函数 .
.
(1)判断f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为2,求a的值.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.
【分析】(1)先确定f(x)的定义域为(0,+∞),再求导,由“f'(x)>0,f(x)为增函数f'(x)<0,f(x)在为减函数”判断,要注意定义域和分类讨论.
(2)因为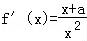 ,x>0.由(1)可知①当a≥0时,f(x)在(0,+∞)上为增函数,f(x)min=f(1)当0<﹣a≤1时,即a≥﹣1时,f(x)在(0,+∞)上也是增函数,f(x)min=f(1)③当1<﹣a<e时,即﹣e<a<﹣1时,f(x)在[1,﹣a]上是减函数,在(﹣a,e]上是增函数,f(x)min=f(﹣a)④当﹣a≥e时,即a≤﹣e时,f(x)在[1,e]上是减函数,f(x)min=f(e)最后取并集.
,x>0.由(1)可知①当a≥0时,f(x)在(0,+∞)上为增函数,f(x)min=f(1)当0<﹣a≤1时,即a≥﹣1时,f(x)在(0,+∞)上也是增函数,f(x)min=f(1)③当1<﹣a<e时,即﹣e<a<﹣1时,f(x)在[1,﹣a]上是减函数,在(﹣a,e]上是增函数,f(x)min=f(﹣a)④当﹣a≥e时,即a≤﹣e时,f(x)在[1,e]上是减函数,f(x)min=f(e)最后取并集.
【解答】解:(1)由题意得f(x)的定义域为(0,+∞),.(0,+∞)
①当a≥0时,f'(x)>0,故f(x)在上为增函数;
②当a<0时,由f'(x)=0得x=﹣a;由f'(x)>0得x>﹣a;由f'(x)<0得x<﹣a;
∴f(x)在(0,﹣a]上为减函数;在(﹣a,+∞)上为增函数.
所以,当a≥0时,f(x)在(0,+∞)上是增函数;当a<0时,f(x)在(0,﹣a]上是减函数,在(﹣a,+∞)上是增函数.
(2)∵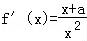 ,x>0.由(1)可知:
,x>0.由(1)可知:
①当a≥0时,f(x)在(0,+∞)上为增函数,f(x)min=f(1)=﹣a=2,得a=﹣2,矛盾!
②当0<﹣a≤1时,即a≥﹣1时,f(x)在(0,+∞)上也是增函数,f(x)min=f(1)=﹣a=2,∴a=﹣2(舍去).
③当1<﹣a<e时,即﹣e<a<﹣1时,f(x)在[1,﹣a]上是减函数,在(﹣a,e]上是增函数,
∴f(x)min=f(﹣a)=ln(﹣a)+1=2,得a=﹣e(舍去).
④当﹣a≥e时,即a≤﹣e时,f(x)在[1,e]上是减函数,有 ,
,
∴a=﹣e.
综上可知:a=﹣e.