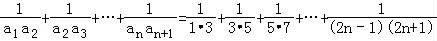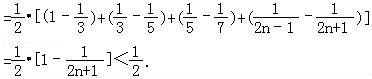“x=1”是“(x﹣1)(x﹣2)=0”的( )
A.必要但不充分条件 B.充分但不必要条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
B
【考点】必要条件、充分条件与充要条件的判断.
【分析】解方程,根据充分必要条件的定义判断即可.
【解答】解:由“(x﹣1)(x﹣2)=0”,解得:x=1或x=2,
故“x=1”是“(x﹣1)(x﹣2)=0”的充分不必要条件,
故选:B.
等差数列{an}中,a7+a9=16,a4=1,则a12=( )
A.15 B.30 C.31 D.64
知识点:2.等差数列及其性质
A
【考点】等差数列的性质.
【分析】由a7+a9=16可得 2a1+14d=16,再由a4=1=a1+3d,解方程求得a1和公差d的值,从而求得a12的值.
【解答】解:设公差等于d,由a7+a9=16可得 2a1+14d=16,即 a1+7d=8.
再由a4=1=a1+3d,可得 a1=﹣ ,d=
,d= .
.
故 a12 =a1+11d=﹣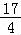 +
+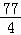 =15,
=15,
故选:A.
在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
A.4 B.
B. C.4
C.4 D.
D.
知识点:9.正弦定理和余弦定理(解三角形)
A
【考点】正弦定理.
【分析】先求得A,进而利用正弦定理求得b的值.
【解答】解:A=180°﹣B﹣C=45°,
由正弦定理知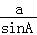 =
=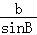 ,
,
∴b=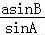 =
=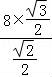 =4
=4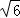 ,
,
故选A.
命题“存在x∈Z使x2+2x+m≤0”的否定是( )
A.存在x∈Z使x2+2x+m>0 B.不存在x∈Z使x2+2x+m>0
C.对任意x∈Z使x2+2x+m≤0 D.对任意x∈Z使x2+2x+m>0
知识点:7.全称量词与存在量词
D
【考点】命题的否定.
【分析】根据命题“存在x∈Z使x2+2x+m≤0”是特称命题,其否定命题是全称命题,将“存在”改为“任意的”,“≤“改为“>”可得答案.
【解答】解:∵命题“存在x∈Z使x2+2x+m≤0”是特称命题
∴否定命题为:对任意x∈Z使x2+2x+m>0
故选D.
如果a>b,给出下列不等式:(1) <
< ;(2)a3>b3;(3)a2+1>b2+1;(4)2a>2b.其中成立的不等式有( )
;(2)a3>b3;(3)a2+1>b2+1;(4)2a>2b.其中成立的不等式有( )
A.(3)(4) B.(2)(3) C.(2)(4) D.(1)(3)
知识点:1.不等式关系与不等式
C
【考点】不等式的基本性质.
【分析】(1)取a=2,b=﹣1,满足a>b,但是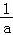 <
<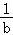 不成立;
不成立;
(2)利用函数f(x)=x3在R上单调递增即可得出;
(3)取a=1,b=﹣2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增即可得出.
【解答】解:(1)取a=2,b=﹣1,满足a>b,但是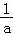 <
<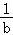 不成立;
不成立;
(2)利用函数f(x)=x3在R上单调递增可得:a3>b3;
(3)取a=1,b=﹣2,满足a>b,但是a2+1>b2+1不成立;
(4)利用指数函数f(x)=2x在R上单调递增可得:2a>2b.
其中成立的不等式有(2)(4).
故选:C.
数列{an}是等差数列,若 <﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
<﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
A.11 B.17 C.19 D.21
知识点:3.等差数列的前n项和
C
【考点】等差数列的性质.
【分析】根据题意判断出d<0、a10>0>a11、a10+a11<0,利用前n项和公式和性质判断出S20<0、S19>0,再利用数列的单调性判断出当Sn取的最小正值时n的值.
【解答】解:由题意知,Sn有最大值,所以d<0,
因为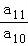 <﹣1,所以a10>0>a11,
<﹣1,所以a10>0>a11,
且a10+a11<0,
所以S20=10(a1+a20)=10(a10+a11)<0,
则S19=19a10>0,
又a1>a2>…>a10>0>a11>a12
所以S10>S9>…>S2>S1>0,S10>S11>…>S19>0>S20>S21
又S19﹣S1=a2+a3+…+a19=9(a10+a11)<0,
所以S19为最小正值,
故选:C.
在△ABC中,若c=2acosB,则△ABC的形状为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.锐角三角形
知识点:9.正弦定理和余弦定理(解三角形)
B
【考点】正弦定理.
【分析】首先利用余弦定理代入已知条件,再根据化简的最终形式,判断三角形的形状.
【解答】解:利用余弦定理: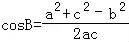
则:c=2acosB=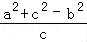
解得:a=b
所以:△ABC的形状为等腰三角形.
故选:B
下列函数中,y的最小值为4的是( )
A.y=x+ B.y=
B.y=
C.y=sin x+ (0<x<π) D.y=ex+e﹣x
(0<x<π) D.y=ex+e﹣x
知识点:4.基本不等式
D
【考点】基本不等式.
【分析】A.x<0时,y<0,不成立;
B.x≤﹣3时,则y≤0,不成立.
C.0<x<π,令sinx=t∈(0,1),则y=t+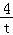 ,利用导数研究函数单调性即可判断出结论.
,利用导数研究函数单调性即可判断出结论.
D.利用基本不等式的性质即可判断出结论.
【解答】解:A.x<0时,y<0,不成立;
B.x≤﹣3时,则y≤0,不成立.
C.∵0<x<π,令sinx=t∈(0,1),则y=t+ ,
,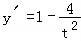 <0,因此函数单调递减,∴y>5,不成立.
<0,因此函数单调递减,∴y>5,不成立.
D.y=ex+e﹣x≥2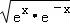 =2,当且仅当x=0时取等号,成立.
=2,当且仅当x=0时取等号,成立.
故选:D.
在坐标平面上,不等式组 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )
A. B.
B. C.
C. D.2
D.2
知识点:3.二元一次不等式(组)与简单的线性规划
B
【考点】二元一次不等式(组)与平面区域.
【分析】作出不等式组对应的平面区域,根据对应图形,求出对应的面积即可.
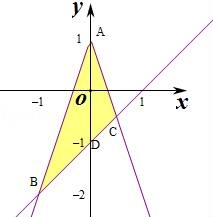
【解答】解:作出不等式组对应的平面区域,
则A(0,1),A到直线y=x﹣1,即x﹣y﹣1=0的距离d=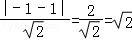 ,
,
由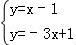 得
得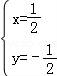 ,即C(
,即C(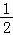 ,﹣
,﹣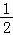 ),
),
由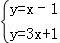 ,得
,得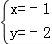 ,即B(﹣1,﹣2),
,即B(﹣1,﹣2),
则|BC|=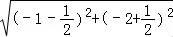 =
=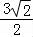 ,
,
则△ABC的面积S=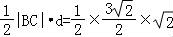 =
=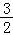 ,
,
故选:B
某游轮在A处看灯塔B在A的北偏东75°,距离为12 海里,灯塔C在A的北偏西30°,距离为8
海里,灯塔C在A的北偏西30°,距离为8 海里,游轮由A向正北方向航行到D处时再看灯塔B在南偏东60°则C与D的距离为( )
海里,游轮由A向正北方向航行到D处时再看灯塔B在南偏东60°则C与D的距离为( )
A.20海里 B.8 海里 C.23
海里 C.23 海里 D.24海里
海里 D.24海里
知识点:9.正弦定理和余弦定理(解三角形)
B
【考点】解三角形的实际应用.
【分析】利用方位角求出B的大小,利用正弦定理直接求解AD的距离,直接利用余弦定理求出CD的距离即可.
【解答】解:如图,在△ABD中,因为在A处看灯塔B在货轮的北偏东75°的方向上,距离为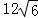 海里,
海里,
货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°方向上,
所以B=180°﹣75°﹣60°=45°,
由正弦定理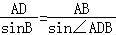 ,
,
所以AD=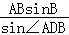 =
=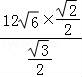 =24海里;
=24海里;
在△ACD中,AD=24,AC=8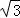 ,∠CAD=30°,
,∠CAD=30°,
由余弦定理可得:CD2=AD2+AC2﹣2•AD•ACcos30°=242+(8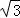 )2﹣2×24×8
)2﹣2×24×8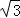 ×
×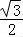 =192,
=192,
所以CD=8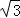 海里;
海里;
故选:B.
设M=a+ (2<a<3).N=x(4
(2<a<3).N=x(4 ﹣3x)(0<x<
﹣3x)(0<x< ),则M,N的大小关系为( )
),则M,N的大小关系为( )
A.M>N B.M<N C.M≥N D.M≤N
知识点:4.基本不等式
A
【考点】基本不等式在最值问题中的应用;不等式比较大小.
【分析】由于M=a+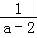 =a﹣2+
=a﹣2+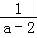 +2(2<a<3)在(2,3)上单调递减,可得M>4,利用基本不等式可求得N的范围,从而可比较二者的大小
+2(2<a<3)在(2,3)上单调递减,可得M>4,利用基本不等式可求得N的范围,从而可比较二者的大小
【解答】解:∵M=a+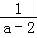 =a﹣2+
=a﹣2+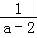 +2,
+2,
而0<a﹣2<1,
又∵y=x+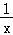 在(0,1]上单调递减,
在(0,1]上单调递减,
∴M在(2,3)上单调递减,
∴M>(3﹣2)+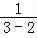 +2=4;
+2=4;
又0<x<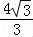 ,
,
∴0<N=x(4﹣3x)=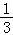 •3x(4﹣3x)≤
•3x(4﹣3x)≤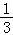 [
[ ]2=
]2=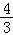 .
.
∴M>N
故选:A
已知f(n)= ,且an=f(n)+f(n+1),则a1+a2+…+a2014的值为( )
,且an=f(n)+f(n+1),则a1+a2+…+a2014的值为( )
A.0 B.2014 C.﹣2014 D.2014×2015
知识点:6.数列的求和
B
【考点】数列的求和.
【分析】由已知条件推出n为奇数时,an+an+1=2,即a1+a2=2,a3+a4=2,…,a2013+a2014=2,由此能求出a1+a2+…+a2014.
【解答】解:∵f(n)=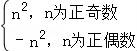 ,且an=f(n)+f(n+1),
,且an=f(n)+f(n+1),
n为奇数时,an=f(n)+f(n+1)=n2﹣(n+1)2=﹣2n﹣1,
an+1=f(n+1)+f(n+2)=﹣(n+1)2+(n+2)2=2n+3,
∴an+an+1=2,
∴a1+a2=2,a3+a4=2,…,a2013+a2014=2,
∴a1+a2+…+a2014
=(a1+a2)+(a3+a4)+…+(a2013+a2014)
=1007×2=2014.
故选:B.
函数y=lg(12+x﹣x2)的定义域是 .
知识点:2.定义域与值域
{x|﹣3<x<4}
【考点】函数的定义域及其求法.
【分析】令12+x﹣x2>0,解不等式即可.
【解答】解:由12+x﹣x2>0,即x2﹣x﹣12<0解得﹣3<x<4.
所以函数的定义域为{x|﹣3<x<4}.
故答案为:{x|﹣3<x<4}.
设a>0,b>0,若 是3a与3b的等比中项,则
是3a与3b的等比中项,则 +
+ 的最小值是 .
的最小值是 .
知识点:4.等比数列及其性质
4
【考点】基本不等式在最值问题中的应用.
【分析】先根据等比中项的性质求得a+b的值,进而利用基本不等式取得ab的最大值,把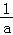 +
+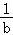 化简整理,根据ab的范围,求得答案.
化简整理,根据ab的范围,求得答案.
【解答】解:∵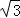 是3a与3b的等比中项
是3a与3b的等比中项
∴3a•3b=3a+b=3
∴a+b=1
∴ab≤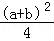 =
=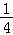 (当a=b时等号成立)
(当a=b时等号成立)
∴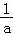 +
+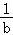 =
=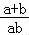 =
=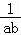 ≥4.
≥4.
故答案为:4
设sin2α=﹣sinα,α∈( ,π),则tan2α的值是 .
,π),则tan2α的值是 .
知识点:4.和角公式与倍(半)角公式
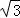
【考点】二倍角的正弦;同角三角函数间的基本关系;二倍角的正切.
【分析】已知等式左边利用二倍角的正弦函数公式化简,根据sinα不为0求出cosα的值,由α的范围,利用同角三角函数间的基本关系求出sinα的值,进而求出tanα的值,所求式子利用二倍角的正切函数公式化简后,将tanα的值代入计算即可求出值.
【解答】解:∵sin2α=2sinαcosα=﹣sinα,α∈(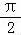 ,π),
,π),
∴cosα=﹣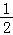 ,sinα=
,sinα=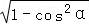 =
=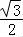 ,
,
∴tanα=﹣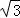 ,
,
则tan2α=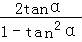 =
= =
= .
.
故答案为:
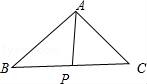
在三角形ABC中,已知AB=4,AC=3,BC=6,P为BC中点,则三角形ABP的周长为 .
知识点:9.正弦定理和余弦定理(解三角形)
7+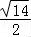
【考点】余弦定理;正弦定理.
【分析】如图所示,设∠APB=α,∠APC=π﹣α.在△ABP与△APC中,由余弦定理可得:AB2=AP2+BP2﹣2AP•BPcosα,AC2=AP2+PC2﹣2AP•PCcos(π﹣α),
可得AB2+AC2=2AP2+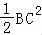 ,代入即可得出.
,代入即可得出.
【解答】解:如图所示,
设∠APB=α,∠APC=π﹣α.
在△ABP与△APC中,
由余弦定理可得:AB2=AP2+BP2﹣2AP•BPcosα,
AC2=AP2+PC2﹣2AP•PCcos(π﹣α),
∴AB2+AC2=2AP2+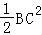 ,
,
∴42+32=2AP2+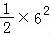 ,
,
解得AP=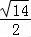 .
.
∴三角形ABP的周长=7+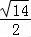 .
.
故答案为:7+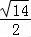 .
.
已知函数f(x)=sin(2x+ )+sin(2x﹣
)+sin(2x﹣ )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ]上的最大值和最小值.
]上的最大值和最小值.
知识点:4.和角公式与倍(半)角公式
【考点】三角函数中的恒等变换应用;三角函数的周期性及其求法;三角函数的最值.
【分析】(1)利用正弦函数的两角和与差的公式与辅助角公式将f(x)=sin(2x+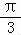 )+sin(2x﹣
)+sin(2x﹣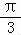 )+2cos2x﹣1化为f(x)=
)+2cos2x﹣1化为f(x)=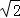 sin(2x+
sin(2x+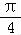 ),即可求得函数f(x)的最小正周期;
),即可求得函数f(x)的最小正周期;
(2)可分析得到函数f(x)在区间[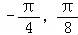 ]上是增函数,在区间[
]上是增函数,在区间[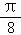 ,
,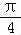 ]上是减函数,从而可求得f(x)在区间[
]上是减函数,从而可求得f(x)在区间[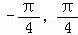 ]上的最大值和最小值.
]上的最大值和最小值.
【解答】解:(1)∵f(x)=sin2x•cos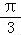 +cos2x•sin
+cos2x•sin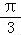 +sin2x•cos
+sin2x•cos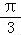 ﹣cos2x•sin
﹣cos2x•sin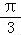 +cos2x
+cos2x
=sin2x+cos2x
=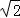 sin(2x+
sin(2x+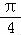 ),
),
∴函数f(x)的最小正周期T= =π.
=π.
(2)∵函数f(x)在区间[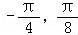 ]上是增函数,在区间[
]上是增函数,在区间[ ,
,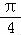 ]上是减函数,
]上是减函数,
又f(﹣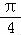 )=﹣1,f(
)=﹣1,f( )=
)=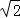 ,f(
,f(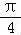 )=1,
)=1,
∴函数f(x)在区间[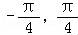 ]上的最大值为
]上的最大值为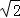 ,最小值为﹣1.
,最小值为﹣1.
解关于x的不等式x2﹣x﹣a(a﹣1)>0.
知识点:2.一元二次不等式及不等式的解法
【考点】一元二次不等式的解法.
【分析】把不等式坐标利用十字相乘法分解因式:(x﹣a)(x+a﹣1)>0,然后对a值进行分类讨论:a与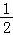 的大小关系三种情况,利用不等式取解集的方法分别求出各自的解集即可.
的大小关系三种情况,利用不等式取解集的方法分别求出各自的解集即可.
【解答】解:原不等式可化为:(x﹣a)(x+a﹣1)>0,
对应方程的根为x1=a,x2=1﹣a…
(1)当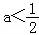 时,有a<1﹣a,解可得x<a或x>1﹣a;…
时,有a<1﹣a,解可得x<a或x>1﹣a;…
(2)当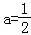 时,a=1﹣a得x∈R且
时,a=1﹣a得x∈R且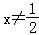 ;…
;…
(3)当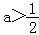 时,a>1﹣a,解可得x<1﹣a或x>a;…
时,a>1﹣a,解可得x<1﹣a或x>a;…
综合得:
(1)当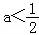 时,原不等式的解集为(﹣∞,a)∪(1﹣a,+∞);
时,原不等式的解集为(﹣∞,a)∪(1﹣a,+∞);
(2)当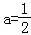 时,原不等式的解集为
时,原不等式的解集为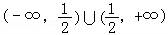 ;
;
(3)当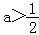 时,原不等式的解集为(﹣∞,1﹣a)∪(a,+∞).…
时,原不等式的解集为(﹣∞,1﹣a)∪(a,+∞).…
已知命题p:方程x2+mx+1=0有两个不相等的实根,命题q:关于x的不等式x2﹣2(m+1)x+m(m+1)>0对任意的实数x恒成立,若“p∨q”为真,“p∧q”为假,求实数m的取值范围.
知识点:6.简单的逻辑联结词
【考点】复合命题的真假.
【分析】若命题p正确,则△>0,解得m范围.若命题q正确,则△<0,解得m范围.若“p∨q”为真,“p∧q”为假,则p与q必然一真一假,即可得出.
【解答】解:命题p:方程x2+mx+1=0有两个不相等的实根,∴△=m2﹣4>0,解得m>2或m<﹣2.
命题q:关于x的不等式x2﹣2(m+1)x+m(m+1)>0对任意的实数x恒成立,∴△=4(m+1)2﹣4m(m+1)<0,解得m<﹣1.
若“p∨q”为真,“p∧q”为假,
则p与q必然一真一假,
∴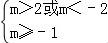 或
或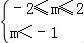 ,
,
解得m>2或﹣2≤m<﹣1.
∴实数m的取值范围是m>2或﹣2≤m<﹣1.
在△ABC中,a、b、c分别是角A、B、C的对边,且 .
.
(1)求角B的大小;
(2)若b= ,且△ABC的面积为
,且△ABC的面积为 ,求a+c的值.
,求a+c的值.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】正弦定理;余弦定理.
【分析】(1)由正弦定理化简已知等式可得2cosBsinA=sin(B+C),由三角形内角和定理即sinA≠0,可得cosB=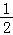 ,又B为三角形的内角,即可解得B的值.
,又B为三角形的内角,即可解得B的值.
(2)由面积公式可解得ac=6,①由余弦定理,可得a2+c2﹣ac=7,即(a+c)2=3ac+7,③将①代入③即可解得a+c的值.
【解答】(本题满分为12分)
解:(1)由正弦定理可得, ,可得2cosBsinA=sin(B+C),
,可得2cosBsinA=sin(B+C),
∵A+B+C=π,
∴2cosBsinA=sinA,
∴cosB=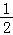 ,
,
∵B为三角形的内角,
∴B=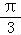 …6分
…6分
(2)b=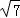 ,B=
,B=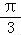 ,由面积公式可得:
,由面积公式可得: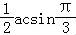 =
= ,即ac=6,①
,即ac=6,①
由余弦定理,可得: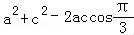 =7,即a2+c2﹣ac=7②,
=7,即a2+c2﹣ac=7②,
由②变形可得:(a+c)2=3ac+7,③
将①代入③可得(a+c)2=25,故解得:a+c=5…12分
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 +
+ +…+
+…+ =1﹣
=1﹣ ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.
知识点:3.等差数列的前n项和
【考点】数列的求和;数列递推式.
【分析】(1)设出等差数列的首项和公差,由已知列式求得首项和公差,则等差数列的通项公式可求;
(2)由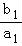 +
+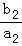 +…+
+…+ =1﹣
=1﹣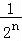 ,求得b1,进一步求得
,求得b1,进一步求得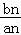 =
=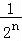 ,得到{bn}的通项公式,再由错位相减法求得数列{bn}的前n项和Tn.
,得到{bn}的通项公式,再由错位相减法求得数列{bn}的前n项和Tn.
【解答】解:(1)设等差数列{an}的首项为a1,公差为d.
由S4=4S2,a2n=2an+1,得
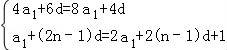 ,
,
解得:a1=1,d=2.
因此an=2n﹣1;
(2)由已知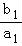 +
+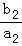 +…+
+…+ =1﹣
=1﹣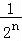 ,n∈N*,
,n∈N*,
当n=1时,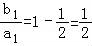 ;
;
当n≥2时,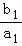 +
+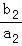 +…+
+…+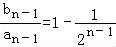 ,
,
∴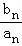 =1﹣
=1﹣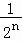 ﹣(1﹣
﹣(1﹣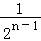 )=
)=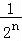 ,
,
∴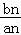 =
=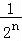 ,n∈N*.
,n∈N*.
由(1)知an=2n﹣1,n∈N*,
∴bn=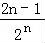 ,n∈N*.
,n∈N*.
又Tn=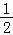 +
+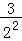 +
+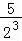 +…+
+…+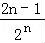 ,
,
∴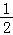 Tn=
Tn=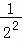 +
+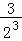 +…+
+…+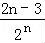 +
+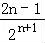 ,
,
两式相减得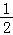 Tn=
Tn=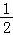 +2(
+2(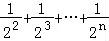 )﹣
)﹣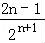
=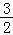 ﹣
﹣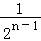 ﹣
﹣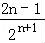 ,
,
∴Tn=3﹣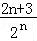 .
.
设各项均为正数的数列{an}的前n项和为Sn,满足4Sn=an+12﹣4n﹣1,n∈N*,且a2,a5,a14构成等比数列.
(1)证明:a2= ;
;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
.
知识点:4.等比数列及其性质
【考点】数列与不等式的综合;等差数列与等比数列的综合.
【分析】(1)对于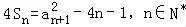 ,令n=1即可证明;
,令n=1即可证明;
(2)利用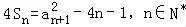 ,且
,且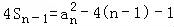 ,(n≥2),两式相减即可求出通项公式.
,(n≥2),两式相减即可求出通项公式.
(3)由(2)可得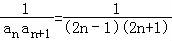 =
= .利用“裂项求和”即可证明.
.利用“裂项求和”即可证明.
【解答】解:(1)当n=1时, ,
,
∵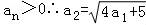
(2)当n≥2时,满足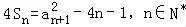 ,且
,且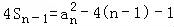 ,
,
∴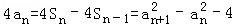 ,
,
∴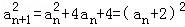 ,
,
∵an>0,∴an+1=an+2,
∴当n≥2时,{an}是公差d=2的等差数列.
∵a2,a5,a14构成等比数列,∴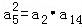 ,
,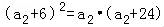 ,解得a2=3,
,解得a2=3,
由(1)可知,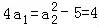 ,∴a1=1∵a2﹣a1=3﹣1=2,
,∴a1=1∵a2﹣a1=3﹣1=2,
∴{an}是首项a1=1,公差d=2的等差数列.
∴数列{an}的通项公式an=2n﹣1.
(3)由(2)可得式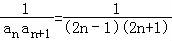 =
= .
.
∴