已知R是实数集, ,则N∩∁RM=( )
,则N∩∁RM=( )
A.(1,2) B.[0,2] C.∅ D.[1,2]
知识点:3.集合的基本运算
D
考点: 交、并、补集的混合运算.
专题: 计算题.
分析: 先化简两个集合M、N到最简形式求出M,N,依照补集的定义求出CRM,再按照交集的定义求出N∩CRM.
解答: 解:∵M={x|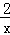 <1}={x|x<0,或x>2},N={y|y=
<1}={x|x<0,或x>2},N={y|y=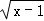 +1}={y|y≥1 },
+1}={y|y≥1 },
CRM={x|0≤x≤2},
故有 N∩CRM={y|y≥1 }∩{x|0≤x≤2}
=[1,+∞)∩[0,2]
=[1,2],
故选D.
点评: 本题考查函数的值域求法,不等式的解法,以及求集合的补集和交集的方法.
设复数z的共轭复数为 ,若z=1﹣i(i为虚数单位),则
,若z=1﹣i(i为虚数单位),则 的值为( )
的值为( )
A.i B.﹣i C.0 D.﹣3i
知识点:3.复数代数形式的四则运算
B
考点: 复数代数形式的混合运算.
专题: 计算题.
分析: 先求出 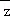 ,再利用两个复数代数形式的乘法法则和虚数单位i的幂运算性质计算
,再利用两个复数代数形式的乘法法则和虚数单位i的幂运算性质计算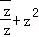 值.
值.
解答: 解:∵复数z=1﹣i(i为虚数单位),
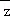 是z的共轭复数,∴
是z的共轭复数,∴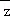 =1+i,
=1+i,
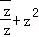 =
=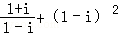 =i﹣2i=﹣i
=i﹣2i=﹣i
故选B.
点评: 本题考查两个复数代数形式的乘法,复数的共轭复数的概念,虚数单位i的幂运算性质.计算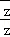 值是解题的关键.
值是解题的关键.
方程2﹣x+x2=3的实数解的个数为( )
A.2 B.3 C.1 D.4
知识点:13.函数与方程
A
考点: 根的存在性及根的个数判断.
专题: 数形结合;转化思想.
分析: 利用 方程2﹣x+x2=3的实数解的个数就等于函数y=2﹣x 与 y=3﹣x2 的图象交点的个数.
解答: 解:如图:考查函数y=2﹣x 与 y=3﹣x2 的图象特征知,
这两个函数的图象有两个交点,
故方程2﹣x+x2=3的实数解的个数为2,
故选A.
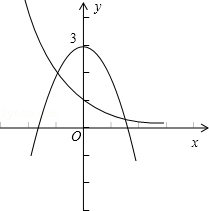
点评: 本题考查方程根的个数判断方法,体现了等价转化的数学思想.
若等差数列{an}的前n项和为Sn,且S4=S18,则S22=( )
A.0 B.12 C.﹣1 D.﹣12
知识点:3.等差数列的前n项和
A
考点: 等差数列的前n项和.
专题: 计算题.
分析: 由S4=S18,可得且S18﹣S4=0,结合等差数列的性质可得(a5+a18)=0,代入等差数列的求和公式S22=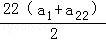 =11(a5+a18)即可求解
=11(a5+a18)即可求解
解答: 解:由S4=S18,可得且S18﹣S4=a5+a6+…+a17+a18
由等差数列的性质可得,7(a5+a18)=0
∴(a5+a18)=0
则S22=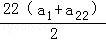 =11(a5+a18)=0
=11(a5+a18)=0
故选A
点评: 本题主要考查了等差数列的性质及等差数列的求和公式的灵活应用,属于基础试题
已知条件p:|x+1|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
A.a≥1 B.a≤1 C.a≥﹣1 D.a≤﹣3
知识点:5.充分条件与必要条件
A
考点: 必要条件、充分条件与充要条件的判断.
专题: 简易逻辑.
分析: 根据充分条件和必要条件的定义,转化为对应的不等式关系进行求解即可.
解答: 解:由|x+1|≤2得﹣3≤x≤1,即p:﹣3≤x≤1,
若p是q的充分不必要条件,
则a≥1,
故选:A.
点评: 本题主要考查充分条件和必要条件的判断,比较基础.
下列命题中是假命题的是( )
A.∀a,b∈R+,lg(a+b)≠lga+lgb
B.∃φ∈R,函数f(x)=sin(2x+φ)是偶函数
C.∃α,β∈R,使得cos(α+β)=cosα+cosβ
D.∃m∈R,使f(x)=(m﹣1)• 是幂函数,且在(0,+∞)上递减
是幂函数,且在(0,+∞)上递减
知识点:6.三角函数的图像与性质
A
考点: 命题的真假判断与应用;全称命题;特称命题.
专题: 简易逻辑.
分析: 利用反例判断A的正误;通过特殊值判断B的正误;特殊值判断C的正误;利用幂函数的定义判断D的正误;
解答: 解:∀a,b∈R+,lg(a+b)≠lga+lgb,如果a=b=2,两个数值相等,所以A不正确.
∃φ∈R,函数f(x)=sin(2x+φ)是偶函数,当φ=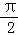 时,函数是偶函数,所以B正确.
时,函数是偶函数,所以B正确.
∃α,β∈R,使得cos(α+β)=cosα+cosβ,例如α=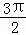 ,β=
,β=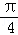 ,等式成立,所以C正确;
,等式成立,所以C正确;
∃m∈R,使f(x)=(m﹣1)•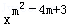 是幂函数,且在(0,+∞)上递减,m=2时函数是幂函数,f(x)=x﹣1.满足题意,正确.
是幂函数,且在(0,+∞)上递减,m=2时函数是幂函数,f(x)=x﹣1.满足题意,正确.
故选:A.
点评: 本题考查命题的真假的判断与应用,反例法与特殊值法是常用方法,考查基本知识的应用.
设二次函数f(x)=ax2﹣4x+c(x∈R)的值域为[0,+∞),则 的最小值为( )
的最小值为( )
A.3 B. C.5 D.7
C.5 D.7
知识点:6.二次函数
A
考点: 基本不等式.
专题: 不等式的解法及应用.
分析: 先判断a、c是正数,且ac=4,把所求的式子变形使用基本不等式求最小值.
解答: 解:由题意知,a>0,△=1﹣4ac=0,∴ac=4,c>0,
则 则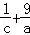 ≥2×
≥2×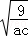 =3,当且仅当
=3,当且仅当 时取等号,
时取等号,
则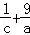 的最小值是 3.
的最小值是 3.
故选A.
点评: 本题考查函数的值域及基本不等式的应用,求解的关键就是拆项,属于基础题.
定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0, )时,f(x)=log
)时,f(x)=log (1﹣x),则f(x)在区间(1,
(1﹣x),则f(x)在区间(1, )内是( )
)内是( )
A.是减函数,且f(x)>0 B.是减函数,且f(x)<0
C.是增函数,且f(x)>0 D.是增函数,且f(x)<0
知识点:5.奇偶性与周期性
C
考点: 函数奇偶性的性质.
专题: 计算题;函数的性质及应用.
分析: 令x∈x∈(1,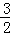 ),则x﹣1∈(0,
),则x﹣1∈(0,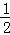 ),利用已知表达式及函数的奇偶性知f(x)=﹣log2(2﹣x),从而可得答案.
),利用已知表达式及函数的奇偶性知f(x)=﹣log2(2﹣x),从而可得答案.
解答: 解:设x∈(1,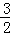 ),则x﹣1∈(0,
),则x﹣1∈(0,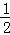 ),
),
根据题意,f(x)=f(﹣x+1)=﹣f(x﹣1)
=﹣log2(1﹣x+1)
=﹣log2(2﹣x),
∴f(x)在区间(1,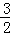 )内是增函数,且f(x)>0.
)内是增函数,且f(x)>0.
故选:C.
点评: 本题考查了函数奇偶性、单调性,考查学生分析解决问题的能力,属于基础题.
已知三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )
A. B.
B. C.
C. D.
D.
知识点:11.球
C
考点: 球内接多面体;点、线、面间的距离计算.
专题: 空间位置关系与距离.
分析: 通过球的内接体,说明几何体的侧面对角线是球的直径,求出球的半径.
解答: 解:因为三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,
所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面B1BCC1,经过球的球心,球的直径是其对角线的长,
因为AB=3,AC=4,BC=5,BC1=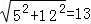 ,
,
所以球的半径为: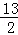 .
.
故选C.
点评: 本题考查球的内接体与球的关系,球的半径的求解,考查计算能力.
设P为等边△ABC所在平面内的一点,满足 ,若AB=1,则
,若AB=1,则 的值为( )
的值为( )
A.4 B.3 C.2 D.1
知识点:4.平面向量的数量积(夹角、模)
B
考点: 向量在几何中的应用.
专题: 计算题.
分析: 先利用三角形法则把所求问题用已知条件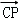 表示出来,整理为用三角形边长和角度表示的等式,再代入已知条件即可求出结论.
表示出来,整理为用三角形边长和角度表示的等式,再代入已知条件即可求出结论.
解答: 解:因为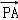 •
•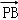 =(
=(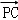 +
+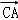 )•(
)•(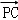 +
+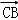 )
)
=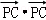 +
+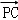 •(
•(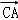 +
+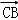 )+
)+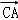 •
•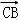
=(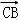 +2
+2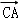 )•(
)•(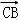 +2
+2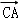 )﹣(
)﹣(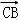 +2
+2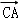 )•(
)•(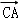 +
+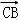 )+
)+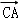 •
•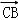
=2 +2
+2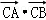
=2×12+2×1×1×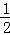
=3.
故选 B.
点评: 本题主要考查向量在几何中的应用中的三角形法则.
在解决向量问题中,三角形法则和平行四边形法则是很常用的转化方法.
一个空间几何体的三视图如图所示,则该几何体的体积为( )

A. B.
B. C.40 D.80
C.40 D.80
知识点:2.空间几何体的三视图和直观图
A
考点: 由三视图求面积、体积.
专题: 计算题;空间位置关系与距离.
分析: 几何体为其中一个侧面在下面的四棱锥,结合直观图判断棱锥的高及底面相关线段的长,把数据代入棱锥的体积公式计算.
解答: 解:由三视图知:几何体为其中一个侧面在下面的四棱锥,如图:
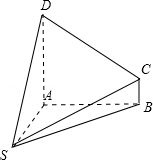
其中SA⊥平面ABCD,SA=4,底面ABCD为直角梯形,且AD=4,BC=1,AB=4,
∴几何体的体积V=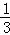 ×
×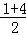 ×4×4=
×4×4=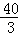 .
.
故选:A.
点评: 本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键.
设函数f(x)=loga(x﹣a+2)在区间(1,+∞)上恒为正值,则实数a的取值范围是( )
A.(1,2] B.(1,2) C.(0,1)∪(1,2) D.
知识点:10.对数函数及其性质
A
考点: 对数函数的单调性与特殊点.
专题: 函数的性质及应用.
分析: 由条件利用对数函数的定义域、单调性和特殊点,可得a>1,且1﹣a+2≥1,由此求得a的范围.
解答: 解:由题意可得a>1,且1﹣a+2≥1,求得1<a≤2,
故选:A.
点评: 本题主要对数函数的定义域、单调性和特殊点,属于基础题.
已知数列{an}中,a1=1,an+1=an+n﹣1,则a6= .
知识点:1.数列的概念与表示方法
11
考点: 数列递推式.
专题: 等差数列与等比数列.
分析: an+1=an+n﹣1,可得当n≥2时,an﹣an﹣1=n﹣2.利用an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1即可得出.
解答: 解:∵an+1=an+n﹣1,
∴当n≥2时,an﹣an﹣1=n﹣2.
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=(n﹣2)+(n﹣3)+…+1+0+1
=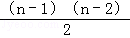 +1,
+1,
=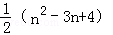 ,
,
∴a6=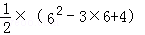 =11.
=11.
故答案为:11.
点评: 本题考查了等差数列的通项公式及其前n项和公式、递推关系的应用、“累加求和”,考查了变形能力、推理能力与计算能力,属于中档题.
设函数 ,f(x)的单调减区间是 .
,f(x)的单调减区间是 .
知识点:3.导数在研究函数中的应用
(﹣2,0)
考点: 利用导数研究函数的单调性.
专题: 函数的性质及应用.
分析: 求出导函数,令导函数大于0求出x的范围为递增区间,导函数小于0得到f(x)的递减区间.
解答: 解:f′(x)=xex+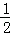 x2ex=
x2ex= x(x+2).
x(x+2).
令 x(x+2)<0得x>0或x<﹣2,
x(x+2)<0得x>0或x<﹣2,
∴f(x)的单增区间为(﹣∞,﹣2)和(0,+∞);
单减区间为(﹣2,0).
故答案为:(﹣2,0)
点评: 求函数的单调区间常利用的工具是导数;导函数的符号判断函数的单调性.
已知向量 与向量
与向量 的夹角为120°,若
的夹角为120°,若 且
且 ,则
,则 在
在 上的投影为 .
上的投影为 .
知识点:4.平面向量的数量积(夹角、模)
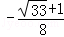
考点: 数量积判断两个平面向量的垂直关系.
专题: 平面向量及应用.
分析: 因为向量 与向量
与向量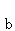 的夹角为120°,所以
的夹角为120°,所以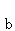 在
在 上的投影为
上的投影为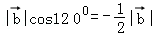 ,问题转化为求
,问题转化为求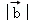 .
.
解答: 解:因为向量 与向量
与向量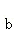 的夹角为120°,
的夹角为120°,
所以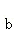 在
在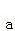 上的投影为
上的投影为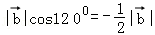 ,
,
问题转化为求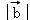 ,
,
因为 ,
,
故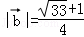 ,
,
所以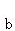 在
在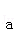 上的投影为
上的投影为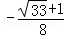 .
.
故答案为: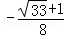 .
.
点评: 本题考查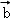 在
在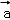 上的投影的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.
上的投影的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.
已知f(x)=asin2x+bcos2x(a,b为常数),若对于任意x∈R都有f(x)≥f( ),则方程f(x)=0在区间[0,π]内的解为 .
),则方程f(x)=0在区间[0,π]内的解为 .
知识点:6.三角函数的图像与性质
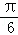 或
或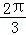
考点: 三角函数中的恒等变换应用.
专题: 三角函数的图像与性质.
分析: 由f(x)≥f(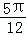 ),可知f(
),可知f(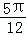 )是函数f(x)的最小值,利用辅助角公式求出a,b的关系,然后利用三角函数的图象和性质进求解即可.
)是函数f(x)的最小值,利用辅助角公式求出a,b的关系,然后利用三角函数的图象和性质进求解即可.
解答: 解:∵f(x)=asin2x+bcos2x=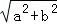 sin(2x+θ)其中tan
sin(2x+θ)其中tan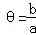 ,
,
由f(x)≥f(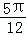 ),则f(
),则f(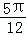 )是函数f(x)的最小值,
)是函数f(x)的最小值,
即f(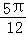 )=
)=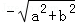 ,
,
∴f(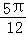 )=
)=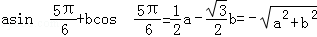 ,
,
即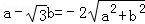 ,
,
平方得, ,
,
即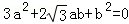 ,
,
∴ ,解得b=﹣
,解得b=﹣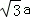 ,
,
∵tan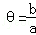 =
=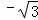 ,不妨设
,不妨设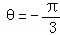 ,
,
则f(x)=asin2x+bcos2x=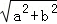 sin(2x﹣
sin(2x﹣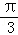 ),
),
由f(x)=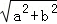 sin(2x﹣
sin(2x﹣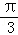 )=0,
)=0,
解得2x﹣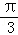 =kπ,
=kπ,
即x=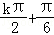 ,k∈Z,
,k∈Z,
∵x∈[0,π],
∴当k=0时,x= ,
,
当k=1时,x=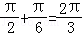 ,
,
故x= 或=
或=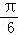 .
.
故答案为: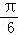 或
或 .
.
点评: 本题主要考查三角函数的图象和性质,利用三角函数的辅助角公式是解决本题的关键,考查学生的计算能力.
(12分)(2015•江门一模)已知函数f(x)=sinωx+ cosωx的最小正周期为π,x∈R,ω>0是常数.
cosωx的最小正周期为π,x∈R,ω>0是常数.
(1)求ω的值;
(2)若f( +
+ )=
)= ,θ∈(0,
,θ∈(0, ),求sin2θ.
),求sin2θ.
知识点:4.和角公式与倍(半)角公式
考点: 三角函数中的恒等变换应用;正弦函数的图象.
专题: 三角函数的求值;三角函数的图像与性质.
分析: (1)由两角和的正弦公式化简解析式可得f(x)=2sin(ωx+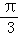 ),由已知及周期公式即可求ω的值.
),由已知及周期公式即可求ω的值.
(2)由已知及三角函数中的恒等变换应用可得f(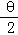 +
+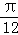 )=2cosθ=
)=2cosθ=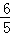 ,可得cosθ,由θ∈(0,
,可得cosθ,由θ∈(0,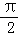 ),可得sinθ,sin2θ的值.
),可得sinθ,sin2θ的值.
解答: 解:(1)∵f(x)=sinωx+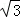 cosωx=2sin(ωx+
cosωx=2sin(ωx+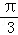 ),
),
∵函数f(x)=sinωx+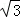 cosωx的最小正周期为π,
cosωx的最小正周期为π,
∴T=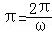 ,解得:ω=2.
,解得:ω=2.
(2)∵f( +
+ )=2sin[2(
)=2sin[2( +
+ )+
)+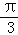 ]=2sin(θ+
]=2sin(θ+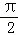 )=2cosθ=
)=2cosθ=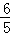 ,
,
∴cosθ= ,
,
∵θ∈(0,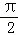 ),
),
∴sin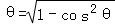 =
=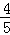 ,
,
∴sin2θ=2sinθcosθ=2×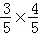 =
=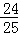 .
.
点评: 本题主要考查了三角函数中的恒等变换应用,正弦函数的周期性,属于基本知识的考查.
(12分)(2015秋•忻州校级月考)已知函数f(x)= ,数列{an}满足a1=1,an+1=f(
,数列{an}满足a1=1,an+1=f( ),(n∈N*),
),(n∈N*),
(1)求数列{an}的通项公式;
(2)设bn= (n≥2),b1=3,求{bn}的前n项和Sn.
(n≥2),b1=3,求{bn}的前n项和Sn.
知识点:6.数列的求和
考点: 数列的求和.
专题: 函数的性质及应用;等差数列与等比数列.
分析: (1)运用等差数列的定义和通项公式,即可得到所求数列的通项;
(2)化简bn=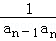 =
=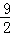 (
(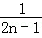 ﹣
﹣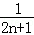 ),再由裂项相消求和,计算即可得到所求.
),再由裂项相消求和,计算即可得到所求.
解答: 解:(1)因an+1=f( )=
)=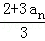 =an+
=an+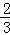 ,
,
所以an+1﹣an=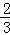 ,
,
故数列{an}是以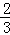 为公差,首项为1的等差数列,
为公差,首项为1的等差数列,
则an= +
+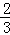 n;
n;
(2)当n≥2时,bn=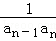 =
=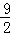 (
(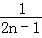 ﹣
﹣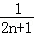 )
)
当n=1时,上式也成立,
所以前n项和Sn=b1+b2+…+bn=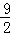 (1﹣
(1﹣ +
+ ﹣
﹣ +…+
+…+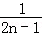 ﹣
﹣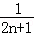 )
)
=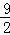 (1﹣
(1﹣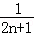 )=
)=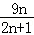 .
.
点评: 本题考查等差数列的定义、通项公式的运用,考查数列的求和方法:裂项相消求和,考查化简运算能力,属于中档题.
(12分)(2015春•忻州校级期末)在△ABC中角A、B、C所对的边分别为a、b、c,面积为S.已知2S=(a+b)2﹣c2
(1)求sinC;
(2)若a+b=10,求S的最大值.
知识点:9.正弦定理和余弦定理(解三角形)
考点: 余弦定理;正弦定理.
专题: 解三角形.
分析: (1)已知等式左边利用三角形面积公式,右边利用完全平方公式展开,变形后利用余弦定理化简,整理求出cosC的值,即可求出sinC的值即可;
(2)利用三角形面积公式列出关系式,把sinC的值代入并利用基本不等式求出ab的最大值,即可求出三角形S的最大值.
解答: 解:(1)∵2S=(a+b)2﹣c2,
∴2×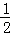 absinC=a2+b2﹣c2+2ab,即
absinC=a2+b2﹣c2+2ab,即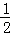 sinC=
sinC=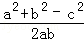 +1,
+1,
由余弦定理可得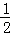 sinC=cosC+1,
sinC=cosC+1,
即5cos2C+8cosC+3=0,
分解因式得:(5cosC+3)(cosC+1)=0,
解得:cosC=﹣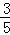 或cosC=﹣1(舍去),
或cosC=﹣1(舍去),
则sinC=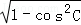 =
=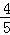 ;
;
(2)∵sinC=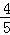 ,
,
∴S=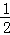 absinC=
absinC=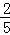 ab≤
ab≤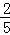 (
(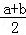 )2=10,
)2=10,
当且仅当a=b=5时“=”成立.
点评: 此题考查了余弦定理,三角形面积公式,以及基本不等式的运用,熟练掌握余弦定理是解本题的关键.
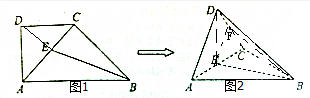
(12分)(2015•河南模拟)如图1所示,直角梯形ABCD,∠ADC=90°,AB∥CD,AD=CD= AB=2,点E为AC的中点,将△ACD沿AC折起,使折起后的平面ACD与平面ABC垂直(如图2),在图2所示的几何体D﹣ABC中.
AB=2,点E为AC的中点,将△ACD沿AC折起,使折起后的平面ACD与平面ABC垂直(如图2),在图2所示的几何体D﹣ABC中.
(1)求证:BC⊥平面ACD;
(2)点F在棱CD上,且满足AD∥平面BEF,求几何体F﹣BCE的体积.
知识点:6.直线、平面垂直的判定及其性质
考点: 棱柱、棱锥、棱台的体积;直线与平面垂直的判定.
专题: 空间位置关系与距离;空间角.
分析: (1)由题意知,AC=BC=2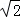 ,从而由勾股定理得AC⊥BC,取AC中点E,连接DE,则DE⊥AC,从而ED⊥平面ABC,由此能证明BC⊥平面ACD.
,从而由勾股定理得AC⊥BC,取AC中点E,连接DE,则DE⊥AC,从而ED⊥平面ABC,由此能证明BC⊥平面ACD.
(2)取DC中点F,连结EF,BF,则EF∥AD,三棱锥F﹣BCE的高h= BC,S△BCE=
BC,S△BCE= S△ACD,由此能求出三棱锥F﹣BCE的体积.
S△ACD,由此能求出三棱锥F﹣BCE的体积.
解答: (1)证明:在图1中,由题意知,AC=BC=2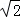 ,
,
∴AC2+BC2=AB2,∴AC⊥BC
取AC中点E,连接DE,则DE⊥AC,
又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DE⊂平面ACD,
从而ED⊥平面ABC,
∴ED⊥BC
又AC⊥BC,AC∩ED=E,
∴BC⊥平面ACD.
(2)解:取DC中点F,连结EF,BF,
∵E是AC中点,∴EF∥AD,
又EF⊂平面BEF,AD⊄平面BEF,∴AD∥平面BEF,
由(1)知,BC为三棱锥B﹣ACD的高,
∵三棱锥F﹣BCE的高h= BC=
BC=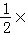 2
2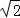 =
=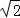 ,
,
S△BCE=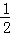 S△ACD=
S△ACD=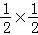 ×2×2=1,
×2×2=1,
所以三棱锥F﹣BCE的体积为:
VF﹣BCE= =
=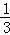 ×1×
×1×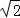 =
=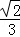 .
.
点评: 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要注意空间思维能力的培养.
(12分)(2015秋•忻州校级月考)已知函数g(x)=bx2+cx+1,f(x)=x2+ax﹣lnx(a>0),g(x)在x=1处的切线方程为y=2x
(1)求b,c的值;
(2)设h(x)=f(x)﹣g(x),是否存在实数a,使得当x∈(0,e]时,函数h(x)的最小值为3,若存在,求出所有满足条件的实数a;若不存在,说明理由.
知识点:3.导数在研究函数中的应用
考点: 利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.
专题: 导数的概念及应用;导数的综合应用.
分析: (1)求出函数g(x)的导数,求得切线的斜率,由已知切线方程,可得2b+c=2,b+c+1=2,解得b,c即可;
(2)求出h(x)的导数,讨论①当a≤0时,②当0<a≤ 时,当a>
时,当a> ,通过单调性判断函数的最值情况,即可判断是否存在.
,通过单调性判断函数的最值情况,即可判断是否存在.
解答: 解:(1)g(x)=bx2+cx+1的导数为g′(x)=2bx+c,
g(x)在x=1处的切线斜率为2b+c,
由g(x)在x=1处的切线为y=2x,
则2b+c=2,b+c+1=2,
解得b=1,c=0;
(2)h(x)=f(x)﹣g(x)=x2+ax﹣lnx+1﹣(x2+1)=ax﹣lnx,
假设存在实数a,使h(x)=ax﹣lnx,x∈(0,e],h有最小值3,
h′(x)=a﹣ ,
,
①当a≤0时,h′(x)<0,
∴h(x)在(0,e]上单调递减,h(x)min=h(e)=ae﹣1=3,
解得a= (舍去),
(舍去),
②当a>0时,h′(x)=a﹣ =
=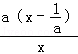 ,
,
(i)当0<a≤ 时,
时, ≥e,h′(x)<0在(0,e]上恒成立,
≥e,h′(x)<0在(0,e]上恒成立,
所以(x)在(0,e]上单调递减,
h(x)min=h(e)=ae﹣1=3,解得a= (舍去),
(舍去),
(ii)当a> 时,0<
时,0< <e,当0<x<
<e,当0<x< 时,h′(x)<0,
时,h′(x)<0,
所以h(x)在(0, )上递减,
)上递减,
当 <x<e时,h′(x)>0,h(x)在(
<x<e时,h′(x)>0,h(x)在( ,e)上递增,
,e)上递增,
所以,h(x)min=h( )=1+lna=3,
)=1+lna=3,
所以a=e2满足条件,
综上,存在a=e2,使当x∈(0,e]时,函数h(x)的最小值为3.
点评: 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查存在性问题的解法,考查运算能力,属于中档题.
(10分)(2015•滕州市校级模拟)选修4﹣4:坐标系与参数方程
已知曲线C1的参数方程为 (其中α为参数),M是曲线C1上的动点,且M是线段OP的中点,(其中O点为坐标原点),P点的轨迹为曲线C2,直线l的方程为ρsin(θ+
(其中α为参数),M是曲线C1上的动点,且M是线段OP的中点,(其中O点为坐标原点),P点的轨迹为曲线C2,直线l的方程为ρsin(θ+ )=
)= ,直线l与曲线C2交于A,B两点.
,直线l与曲线C2交于A,B两点.
(1)求曲线C2的普通方程;
(2)求线段AB的长.
知识点:2.坐标系与参数方程
考点: 参数方程化成普通方程.
专题: 直线与圆.
分析: (1)把曲线C1的参数方乘化为普通方程,设点P的坐标为(x,y),由M 是线段OP 的中点,可得点M的坐标,再把点M的坐标代入C1的普通方程化简可得所求.
(2)求得直线l的直角坐标方程,求出圆心(0,4)到直线的距离d,利用弦长公式求出线段AB 的值.
解答: 解:(1)由曲线C1的参数方程为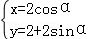 (其中α为参数),消去参数化为普通方程为 x2+(y﹣2)2=4.
(其中α为参数),消去参数化为普通方程为 x2+(y﹣2)2=4.
设点P的坐标为(x,y),由M 是线段OP 的中点,可得点M的坐标为( ,
,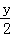 ).
).
再由M是曲线C1上的动点可得 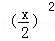 +
+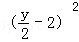 =4,即 x2+(y﹣4)2=16.故曲线C2的普通方程为 x2+(y﹣4)2=16.
=4,即 x2+(y﹣4)2=16.故曲线C2的普通方程为 x2+(y﹣4)2=16.
(2)直线l 的方程为ρsin(θ+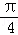 )=
)=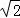 ,即 ρcosθ+ρsinθ=2,即 x+y﹣2=0.
,即 ρcosθ+ρsinθ=2,即 x+y﹣2=0.
由于圆心(0,4)到直线的距离等于d=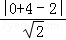 =
=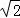 ,圆的半径等于4,
,圆的半径等于4,
∴线段AB=2 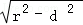 =2
=2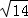 .
.
点评: 本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式、弦长公式的应用,属于基础题.
(2014•海口二模)设函数f(x)=|x﹣ |+|x﹣a|,x∈R.
|+|x﹣a|,x∈R.
(Ⅰ)求证:当a=﹣ 时,不等式lnf(x)>1成立.
时,不等式lnf(x)>1成立.
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值.
知识点:3.不等式选讲
考点: 绝对值不等式的解法.
专题: 不等式的解法及应用.
分析: (Ⅰ)当a=﹣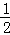 时,根据f(x)=
时,根据f(x)=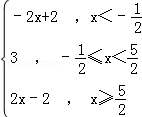 的最小值为3,可得lnf(x)最小值为ln3>lne=1,不等式得证.
的最小值为3,可得lnf(x)最小值为ln3>lne=1,不等式得证.
(Ⅱ)由绝对值三角不等式可得 f(x)≥|a﹣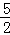 |,可得|a﹣
|,可得|a﹣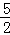 |≥a,由此解得a的范围.
|≥a,由此解得a的范围.
解答: 解:(Ⅰ)证明:∵当a=﹣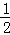 时,f(x)=|x﹣
时,f(x)=|x﹣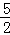 |+|x+
|+|x+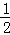 |=
|=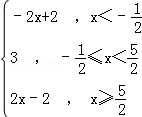 的最小值为3,
的最小值为3,
∴lnf(x)最小值为ln3>lne=1,∴lnf(x)>1成立.
(Ⅱ)由绝对值三角不等式可得 f(x)=|x﹣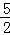 |+|x﹣a|≥|(x﹣
|+|x﹣a|≥|(x﹣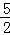 )﹣(x﹣a)|=|a﹣
)﹣(x﹣a)|=|a﹣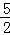 |,
|,
再由不等式f(x)≥a在R上恒成立,可得|a﹣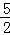 |≥a,
|≥a,
∴a﹣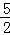 ≥a,或 a﹣
≥a,或 a﹣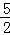 ≤﹣a,解得a≤
≤﹣a,解得a≤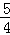 ,故a的最大值为
,故a的最大值为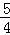 .
.
点评: 本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,函数的恒成立问题,属于基础题.