直线 x+3y+1=0的倾斜角是( )
x+3y+1=0的倾斜角是( )
A. B.
B. C.
C. D.
D.
知识点:1.直线的倾斜角、斜率与方程
D
【考点】直线的倾斜角.
【专题】计算题;直线与圆.
【分析】求出直线的斜率,即可求出直线的倾斜角.
【解答】解:直线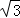 x+3y+1=0的斜率是﹣
x+3y+1=0的斜率是﹣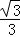 ,倾斜角是
,倾斜角是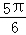 ,
,
故选:D.
【点评】本题考查了直线的倾斜角与斜率的关系,属于基础题.
二圆C1:x2+y2=1和C2:x2+y2﹣4x﹣5=0的位置关系是( )
A.相交 B.外切 C.内切 D.外离
知识点:4.直线与圆的位置关系
C
【考点】圆与圆的位置关系及其判定.
【专题】直线与圆.
【分析】先求出两圆的圆心 和半径,根据两圆的圆心距等于两圆的半径之和,得出两圆相外切.
【解答】解:圆x2+y2﹣4x﹣5=0 即 (x﹣2)2+y2=9,表示以(2,0)为圆心,以3为半径的圆,
两圆的圆心距为2,正好等于两圆的半径之差,故两圆相内切,
故选C.
【点评】本题考查两圆的位置关系,由两圆的圆心距等于两圆的半径之和与差,得出两圆的位置关系.
命题“若a2+b2=0,则a=0且b=0”的逆否命题是( )
A.若a2+b2≠0,则a≠0且b≠0 B.若a2+b2≠0,则a≠0或b≠0
C.若a=0且b=0,则a2+b2≠0 D.若a≠0或b≠0,则a2+b2≠0
知识点:4.命题及其关系
D
【考点】四种命题.
【专题】常规题型.
【分析】若原命题是“若p,则q”,则逆否命题是“若非q,则非p”也就是将命题的条件与结论都否定,再进行互换.由此分别将“a2+b2=0”、“a=0且b=0”否定,得到否命题,再将其改成逆命题,就不难得出正确答案.
【解答】解:∵原命题是若a2+b2=0,则“a=0且b=0”
∴否命题是“若a2+b2≠0,则a≠0或b≠0”
从而得到逆否命题是“若a≠0或b≠0,则a2+b2≠0”
故选D
【点评】本题考查了原命题与逆否命题之间的关系,属于基础题.解题时应该注意含有逻辑词的条件的否定:“p且q”的否定是“非p或非q”.
已知双曲线 的离心率为
的离心率为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A. B.
B. C.y=±2x D.
C.y=±2x D.
知识点:2.双曲线
A
【考点】双曲线的简单性质.
【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】根据题意,得双曲线的渐近线方程为y=±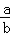 x.再由双曲线离心率为
x.再由双曲线离心率为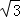 ,得到c=
,得到c=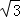 a,由定义知b=
a,由定义知b=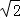 a,代入即得此双曲线的渐近线方程.
a,代入即得此双曲线的渐近线方程.
【解答】解:∵双曲线C方程为: ,
,
∴双曲线的渐近线方程为y=±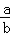 x
x
又∵双曲线离心率为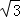 ,
,
∴c=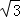 a,可得b=
a,可得b=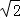 a
a
因此,双曲线的渐近线方程为y=±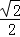 x
x
故选:A.
【点评】本题给出双曲线的离心率,求双曲线的渐近线方程,着重考查了双曲线的标准方程与基本概念,属于基础题.
若抛物线y2=2px的焦点与椭圆 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )
A.﹣2 B.2 C.﹣4 D.4
知识点:1.椭圆
D
【考点】抛物线的简单性质.
【专题】圆锥曲线的定义、性质与方程.
【分析】先根据椭圆方程求出其右焦点的坐标,在于抛物线的性质可确定p的值.
【解答】解:椭圆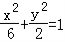 中,
中,
c2=6﹣2=4,即c=2,
故椭圆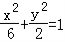 的右焦点为(2,0),
的右焦点为(2,0),
所以抛物线y2=2px的焦点为(2,0),
则p=4,
故选D.
【点评】本题主要考查椭圆的简单性质和抛物线的标准方程,难度不大,属于基础题.
“1<m<2”是“方程 +
+ =1表示的曲线是焦点在y轴上的椭圆”的( )
=1表示的曲线是焦点在y轴上的椭圆”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
C
【考点】必要条件、充分条件与充要条件的判断.
【专题】简易逻辑.
【分析】根据椭圆的性质,结合充分条件和必要条件的定义进行判断即可.
【解答】解:若方程 +
+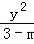 =1表示的曲线是焦点在y轴上的椭圆,
=1表示的曲线是焦点在y轴上的椭圆,
则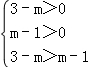 ,
,
即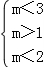 ,
,
解得1<m<2,即“1<m<2”是“方程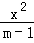 +
+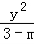 =1表示的曲线是焦点在y轴上的椭圆”的充要条件,
=1表示的曲线是焦点在y轴上的椭圆”的充要条件,
故选:C
【点评】本题主要考查充分条件和必要条件的判断,根据椭圆方程的性质是解决本题的关键.
双曲线C: ﹣
﹣ =1(a>0,b>0)的离心率为2,焦点到渐近线的距离为
=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为 ,则C的焦距等于( )
,则C的焦距等于( )
A.2 B.2 C.4 D.4
C.4 D.4
知识点:2.双曲线
C
【考点】双曲线的简单性质.
【专题】圆锥曲线的定义、性质与方程.
【分析】根据双曲线的离心率以及焦点到直线的距离公式,建立方程组即可得到结论.
【解答】解:∵: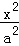 ﹣
﹣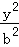 =1(a>0,b>0)的离心率为2,
=1(a>0,b>0)的离心率为2,
∴e=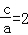 ,双曲线的渐近线方程为y=
,双曲线的渐近线方程为y=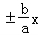 ,不妨取y=
,不妨取y= ,即bx﹣ay=0,
,即bx﹣ay=0,
则c=2a,b=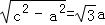 ,
,
∵焦点F(c,0)到渐近线bx﹣ay=0的距离为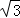 ,
,
∴d=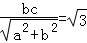 ,
,
即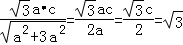 ,
,
解得c=2,
则焦距为2c=4,
故选:C
【点评】本题主要考查是双曲线的基本运算,利用双曲线的离心率以及焦点到直线的距离公式,建立方程组是解决本题的关键,比较基础.
已知圆x2﹣2x+y2﹣2my+2m﹣1=0,当圆的面积最小时,直线y=x+b与圆相切,则b=( )
A.±1 B.1 C. D.
D.
知识点:4.直线与圆的位置关系
C
【考点】圆的切线方程.
【专题】直线与圆.
【分析】求出圆的圆心和半径,由二次函数的最值,可得最小值为1,m=1,再由直线和圆相切的条件:d=r,解方程即可得到b.
【解答】解:圆x2﹣2x+y2﹣2my+2m﹣1=0的圆心为(1,m),半径为r= ,
,
当圆的面积最小时,半径r=1,此时m=1,
即圆心为(1,1),
由直线和圆相切的条件:d=r,可得
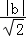 =1,
=1,
解得b=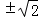 .
.
故选:C.
【点评】本题考查直线与圆的位置关系:相切,主要考查直线和圆相切的条件:d=r,同时考查点到直线的距离,属于基础题.
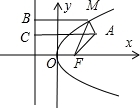
已知点A(3,4),F是抛物线y2=8x的焦点,M是抛物线上的动点,当|MA|+|MF|最小时,M点坐标是( )
A.(0,0) B.(3,2 ) C.(2,4) D.(3,﹣2
) C.(2,4) D.(3,﹣2 )
)
知识点:3.抛物线
C
【考点】抛物线的简单性质.
【专题】圆锥曲线的定义、性质与方程.
【分析】设抛物线的准线为l,过M作MB⊥l于B,过A作AC⊥l于C,利用抛物线的定义,可得结论.
【解答】解:设抛物线的准线为l,过M作MB⊥l于B,过A作AC⊥l于C,
由抛物线定义知|MF|=|MB|⇒|MA|+|MF|=|MA|+|MB|≥|AC|(折线段大于垂线段),当且仅当A,M,C三点共线取等号,即|MA|+|MF|最小.
此时M的纵坐标为4,横坐标为2
所以M(2,4)
故选C.
【点评】本题考查抛物线的定义,考查学生分析解决问题的能力,属于基础题.
下列说法正确的个数为( )
(1)椭圆x2+my2=1的焦点在x轴上,长轴长是短轴长的2倍,则m的值为4.
(2)直线L:ax+y﹣a=0在x轴和y轴上的截距互为相反数,则a的值是﹣1
(3)圆x2+y2=9的弦过点P(1,2),当弦长最短时,圆心到弦的距离为2.
(4)等轴双曲线的离心率为1.
A.2 B.3 C.4 D.1
知识点:1.椭圆
A
【考点】椭圆的简单性质;双曲线的简单性质.
【专题】转化思想;数学模型法;圆锥曲线的定义、性质与方程.
【分析】(1)由题意可得:1=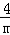 ,解得m,即可判断出;
,解得m,即可判断出;
(2)当a=0时,y=0,不满足题意;当a≠0时,直线方程化为x+ =1,则a的值是﹣1,即可判断出正误;
=1,则a的值是﹣1,即可判断出正误;
(3)当弦长AB最短时,AB⊥OP,圆心到弦的距离d=OP,利用两点之间的距离个数即可得出.
(4)等轴双曲线的离心率为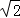 .
.
【解答】解:(1)椭圆x2+my2=1即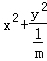 =1的焦点在x轴上,长轴长是短轴长的2倍,1=
=1的焦点在x轴上,长轴长是短轴长的2倍,1=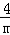 ,解得m=4,正确;
,解得m=4,正确;
(2)直线L:ax+y﹣a=0在x轴和y轴上的截距互为相反数,当a=0时,y=0,不满足题意;当a≠0时,直线方程化为x+ =1,则a的值是﹣1,正确;
=1,则a的值是﹣1,正确;
(3)圆x2+y2=9的弦过点P(1,2),当弦长AB最短时,AB⊥OP,圆心到弦的距离d=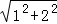 =
=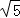 ,因此不正确.
,因此不正确.
(4)等轴双曲线的离心率为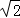 ,因此不正确.
,因此不正确.
综上可得:正确命题的个数为2.
故选:A.
【点评】本题考查了圆锥曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.
若椭圆 的离心率
的离心率 ,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )
,右焦点为F(c,0),方程ax2+2bx+c=0的两个实数根分别是x1和x2,则点P(x1,x2)到原点的距离为( )
A. B.
B. C.2 D.
C.2 D.
知识点:1.椭圆
A
【考点】椭圆的简单性质;一元二次方程的根的分布与系数的关系;两点间距离公式的应用.
【专题】计算题.
【分析】利用一元二次方程根与系数的关系求出 x1 +x2 和x1 •x2 的值,再利用椭圆的简单性质求出P(x1,x2)到原点的距离.
【解答】解:由题意知 x1 +x2 =﹣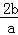 =﹣2
=﹣2 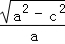 ,∴(x1+x2)2=4(1﹣e2)=3 ①,
,∴(x1+x2)2=4(1﹣e2)=3 ①,
x1 •x2 =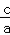 =
=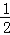 ②,由①②解得 x12+x22=2,故P(x1,x2)到原点的距离为
②,由①②解得 x12+x22=2,故P(x1,x2)到原点的距离为 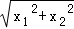 =
=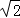 ,
,
故选 A.
【点评】本题考查一元二次方程根与系数的关系,两点间的距离公式,椭圆的标准方程,以及椭圆的简单性质的应用.
已知点F(﹣c,0)(c>0)是双曲线 的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则e2=( )
的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则e2=( )
A. B.
B. C.
C. D.
D.
知识点:2.双曲线
D
【考点】双曲线的简单性质.
【专题】计算题;圆锥曲线的定义、性质与方程.
【分析】利用抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质、相似三角形的性质即可得出.
【解答】解:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,
设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=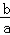 ,|FF′|=2c,
,|FF′|=2c,
满足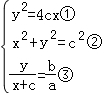 ,
,
将①代入②得x2+4cx﹣c2=0,
则x=﹣2c± c,
c,
即x=( ﹣2)c,(负值舍去)
﹣2)c,(负值舍去)
代入③,即y= ,再将y代入①得,
,再将y代入①得, =e2﹣1
=e2﹣1
即e2=1+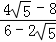 =
=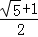 .
.
故选:D.

【点评】本题考查双曲线的性质,掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键.
设y2=4px(p>0)上横坐标为6的点到焦点的距离为10,则抛物线的解析式 .
知识点:3.抛物线
y2=16x
【考点】抛物线的简单性质.
【专题】方程思想;定义法;圆锥曲线的定义、性质与方程.
【分析】求得抛物线的焦点和准线的方程,运用抛物线的定义可得横坐标为6的点到焦点的距离为10,即有横坐标为6的点到准线的距离为10,解方程可得p=4,进而得到抛物线的方程.
【解答】解:y2=4px(p>0)的焦点为(p,0),
准线方程为x=﹣p,
由抛物线的定义可得,横坐标为6的点到焦点的距离为10,
即有横坐标为6的点到准线的距离为10,
即6+p=10,解得p=4,
则抛物线的方程为y2=16x,
故答案为:y2=16x.
【点评】本题考查抛物线的解析式的求法,注意运用抛物线的定义,考查运算能力,属于基础题.
过直线L:x+y﹣2=0上一动点P作圆O:x2+y2=1两切线,切点分别为A,B,则四边形OAPB面积的最小值为 .
知识点:4.直线与圆的位置关系
1
【考点】直线与圆的位置关系;圆的切线方程.
【专题】计算题;转化思想;综合法;直线与圆.
【分析】四边形PAOB为2个对称的直角三角形构成,由OA与OB为圆的半径,其值固定不变,得到当PO最小值,四边形PAOB的面积最小,即圆心到直线的距离最小,利用点到直线的距离公式求出PO的长,利用勾股定理求出此时AP的长,利用三角形的面积公式求出两直角三角形的面积,即为四边形PAOB面积的最小值.
【解答】解:由圆x2+y2=1,得到圆心O坐标为(0,0),半径r=1,
又直线x+y﹣2=0,
∴|PO|min=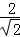 =
=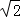 ,又|OA|=1,
,又|OA|=1,
∴在Rt△AOP中,利用勾股定理得:|AP|=1,
则四边形PAOB面积的最小值S=2×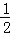 ×|OA|×|AP|=1.
×|OA|×|AP|=1.
故答案为:1.
【点评】此题考查了直线与圆方程的应用,涉及的知识有:圆的标准方程,点到直线的距离公式,勾股定理,以及三角形面积的求法,其中根据题意得到|PO|的最小时,Rt△APO面积最小是解本题的关键.
设F1,F2是双曲线 的两个焦点,P是双曲线与椭圆
的两个焦点,P是双曲线与椭圆 的一个公共点,则△PF1F2的面积等于 .
的一个公共点,则△PF1F2的面积等于 .
知识点:1.椭圆
24
【考点】双曲线的简单性质.
【专题】圆锥曲线的定义、性质与方程.
【分析】由题意,|F1F2|=10,椭圆 与双曲线
与双曲线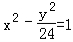 共焦点,利用椭圆、双曲线的定义,求出△PF1F2的三边,即可求其面积.
共焦点,利用椭圆、双曲线的定义,求出△PF1F2的三边,即可求其面积.
【解答】解:由题意,|F1F2|=10,椭圆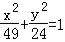 与双曲线
与双曲线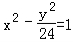 共焦点
共焦点
∵P是双曲线与椭圆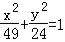 的一个公共点,(不妨设是右支上一点)
的一个公共点,(不妨设是右支上一点)
∴|PF1|+|PF2|=14,|PF1|﹣|PF2|=2,
∴|PF1|=8,|PF2|=6,
∵|F1F2|=10,
∴△PF1F2是直角三角形,
∴△PF1F2的面积等于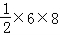 =24.
=24.
故答案为:24.
【点评】本题考查三角形面积的计算,考查椭圆、双曲线的定义,求出△PF1F2的三边是关键.
下面给出的四个命题中:
①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为(x﹣1)2+y2=1;
②点(1,2)关于直线L:X﹣Y+2=0对称的点的坐标为(0,3).
③命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”;
④命题:过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有2条.
其中是真命题的有 (将你认为正确的序号都填上).
知识点:3.抛物线
①②③
【考点】命题的真假判断与应用.
【专题】方程思想;转化思想;圆锥曲线的定义、性质与方程;简易逻辑.
【分析】①以抛物线y2=4x的焦点(1,0)为圆心,且过坐标原点的圆的半径为1,可得原点方程,即可判断出正误;
②设点(1,2)关于直线L:X﹣Y+2=0对称的点的坐标为(x,y),则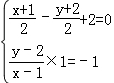 ,解得即可判断出正误.
,解得即可判断出正误.
③利用命题的否定定义即可判断出正误;
④这样的直线有3条,分别为x=0,y=1,y=x+1,即可判断出正误.
【解答】解:①以抛物线y2=4x的焦点(1,0)为圆心,且过坐标原点的圆的方程为(x﹣1)2+y2=1,正确;
②设点(1,2)关于直线L:X﹣Y+2=0对称的点的坐标为(x,y),则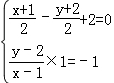 ,解得
,解得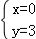 ,因此所求对称点为(0,3),正确.
,因此所求对称点为(0,3),正确.
③命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”,正确;
④命题:过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有3条,分别为x=0,y=1,y=x+1,因此不正确.
其中是真命题的有①②③.
故答案为:①②③.
【点评】本题考查了圆锥曲线的判定方法、命题真假的判定方法,考查了推理能力与计算能力,属于中档题.
已知直线l1:3x+4y﹣2=0与l2:2x+y+2=0的交点为P.
(Ⅰ)求交点P的坐标;
(Ⅱ)求过点P且平行于直线l3:x﹣2y﹣1=0的直线方程;
(Ⅲ)求过点P且垂直于直线l3:x﹣2y﹣1=0直线方程.
知识点:1.直线的倾斜角、斜率与方程
【考点】直线的一般式方程;两条直线的交点坐标.
【专题】计算题.
【分析】(Ⅰ)联立两直线的方程,得到一个关于x与y的二元一次方程组,求出方程组的解即可得到交点P的坐标;
(Ⅱ)根据两直线平行时,斜率相等,由直线l3的斜率设出所求直线的方程为x﹣2y+m=0,把第一问求出的P的坐标代入即可确定出m的值,进而确定出所求直线的方程;
(Ⅲ)根据两直线垂直时,斜率的乘积为﹣1,由直线l3的斜率求出所求直线的斜率,设出所求直线的方程,把P的坐标代入即可确定出所求直线的方程.
【解答】(本小题满分12分)
解:(Ⅰ)由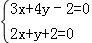 ,解得
,解得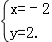 ,
,
所以点P的坐标是(﹣2,2); …
(Ⅱ)因为所求直线与l3平行,
所以设所求直线的方程为 x﹣2y+m=0.
把点P的坐标代入得﹣2﹣2×2+m=0,得m=6.
故所求直线的方程为x﹣2y+6=0; …
(Ⅲ)因为所求直线与l3垂直,
所以设所求直线的方程为 2x+y+n=0.
把点P的坐标代入得 2×(﹣2)+2+n=0,得n=2.
故所求直线的方程为 2x+y+2=0. …
【点评】此题考查了直线的一般式方程,以及两直线的交点坐标,两直线方程的交点坐标的求法为:联立两直线的解析式组成方程组,求出方程组的解可得交点坐标,同时要求学生掌握两直线平行及垂直时斜率满足的关系.
已知双曲线C: =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,实轴长为2;
,实轴长为2;
(1)求双曲线C的标准方程;
(2)已知直线x﹣y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求实数m的值.
知识点:2.双曲线
【考点】直线与圆锥曲线的综合问题.
【专题】圆锥曲线的定义、性质与方程.
【分析】(1)依题意得2a=2,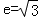 ,由此能求出双曲线方程.
,由此能求出双曲线方程.
(2)设点A(x1,y1),B(x2,y2)AB的中点M(x0,y0),由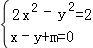 ,得x2﹣2mx﹣m2﹣2=0,由此能求出实数m的值.
,得x2﹣2mx﹣m2﹣2=0,由此能求出实数m的值.
【解答】解:(1)依题意得2a=2,a=1,…
 ,∴
,∴ ,…
,…
∴b2=c2﹣a2=2,…
∴双曲线方程为: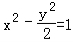 …
…
(2)设点A(x1,y1),B(x2,y2)AB的中点M(x0,y0),…
由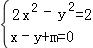 得x2﹣2mx﹣m2﹣2=0…
得x2﹣2mx﹣m2﹣2=0…
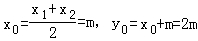 ,…
,…
∵点M在圆上,∴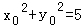 ,
,
∴m2+(2m)2=5,∴m=±1.…
【点评】本题考查双曲线方程的求法,考查实数值的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.
已知圆C经过点A(2,﹣1),和直线x+y=1相切,且圆心在直线y=﹣2x上.
(Ⅰ)求圆C的方程;
(Ⅱ)已知直线l经过原点,并且被圆C截得的弦长为2,求直线l的方程.
知识点:4.直线与圆的位置关系
【考点】直线与圆的位置关系;圆的标准方程.
【专题】综合题;直线与圆.
【分析】(Ⅰ)设出圆心的坐标为(a,﹣2a),利用两点间的距离公式表示出圆心到A的距离即为圆的半径,且根据圆与直线x+y=1相切,根据圆心到直线的距离等于圆的半径列出关于a的方程,求出方程的解得到a的值,确定出圆心坐标,进而求出圆的半径,根据圆心和半径写出圆的标准方程即可.
(Ⅱ)分类讨论,利用被圆C截得的弦长为2,求出直线的斜率,即可求直线l的方程.
【解答】解:(Ⅰ)设所求圆心坐标为(a,﹣2a)
由条件得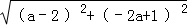 =
=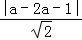 ,化简得a2﹣2a+1=0,
,化简得a2﹣2a+1=0,
∴a=1,
∴圆心为(1,﹣2),半径r=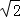
∴所求圆方程为(x﹣1)2+(y+2)2=2
(Ⅱ)①当直线l的斜率不存在时,直线l的方程为x=0,此时直线l被圆C截得的弦长为2,满足条件.
②当直线l的斜率存在时,设直线l的方程为y=kx,
由题得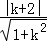 =1,解得k=﹣
=1,解得k=﹣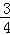 ,∴直线l的方程为y=﹣
,∴直线l的方程为y=﹣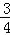 x.
x.
综上所述:直线l的方程为x=0或y=﹣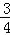 x.
x.
【点评】本题考查了直线与圆的位置关系,涉及的知识有两点间的距离公式,点到直线的距离公式,圆的标准方程,当直线与圆相切时,圆心到直线的距离等于圆的半径,常常利用此性质列出方程来解决问题.
已知椭圆与双曲线 的焦点相同,且它们的离心率之和等于
的焦点相同,且它们的离心率之和等于 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)过椭圆内一点M(1,1)作一条弦AB,使该弦被点M平分,求弦AB所在直线方程.
知识点:1.椭圆
【考点】双曲线的简单性质.
【专题】计算题;直线与圆;圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)求出椭圆的焦点和离心率,进而得到双曲线的离心率和焦点,再由椭圆的a,b,c的关系,即可得到椭圆方程;
(Ⅱ)设出弦AB的端点的坐标,代入椭圆方程和中点坐标公式,运用作差,结合平方差公式和斜率公式,由点斜式方程即可得到直线AB的方程.
【解答】解:(Ⅰ)双曲线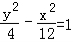 的焦点为(0,4),(0,﹣4),
的焦点为(0,4),(0,﹣4),
离心率为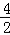 =2,
=2,
则椭圆的方程为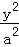 +
+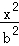 =1(a>b>0),
=1(a>b>0),
且离心率e=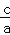 =
=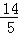 ﹣2=
﹣2=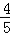 ,
,
由于c=4,则a=5,b= =3,
=3,
则椭圆方程为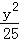 +
+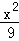 =1;
=1;
(Ⅱ)设A(x1,y1),B(x2,y2),
则x1+x2=2,y1+y2=2,
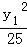 +
+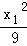 =1,
=1,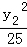 +
+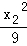 =1,
=1,
两式相减可得,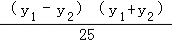 +
+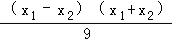 =0,
=0,
即有kAB=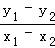 =﹣
=﹣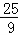 ,
,
则直线AB所在方程为y﹣1=﹣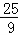 (x﹣1),
(x﹣1),
由于M在椭圆内,则弦AB存在.
则所求直线AB的方程为25x+9y﹣34=0.
【点评】本题考查椭圆和双曲线的方程和性质,考查离心率的求法,考查中点坐标公式和点差法的运用,考查运算能力,属于中档题.
已知椭圆C: +
+ =1(a>b>0)经过点M(1,
=1(a>b>0)经过点M(1, ),其离心率为
),其离心率为 ,设直线l:y=kx+m与椭圆C相交于A、B两点.
,设直线l:y=kx+m与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)已知直线l与圆x2+y2= 相切,求证:OA⊥OB(O为坐标原点).
相切,求证:OA⊥OB(O为坐标原点).
知识点:1.椭圆
【考点】椭圆的简单性质.
【专题】直线与圆;圆锥曲线的定义、性质与方程.
【分析】(1)由离心率及a2=b2+c2,得a与b的关系式,再将点M的坐标代入椭圆方程中,求解关于a,b的二元二次方程组,即得a2,b2,从而得椭圆的标准方程;
(2)根据圆心到直线的距离等于圆的半径,得k与m的等量关系,要证明OA⊥OB,只需证明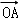 •
•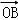 =0即可,从而将数量积转化为坐标运算,联立直线l与椭圆方程,利用韦达定理消去坐标,得到关于k,m的代数式,再利用前面k与m的等量关系即可达到目的.
=0即可,从而将数量积转化为坐标运算,联立直线l与椭圆方程,利用韦达定理消去坐标,得到关于k,m的代数式,再利用前面k与m的等量关系即可达到目的.
【解答】解:(1)由离心率e=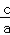 =
=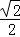 ,a2=b2+c2,a2=2b2,
,a2=b2+c2,a2=2b2,
即有椭圆方程为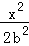 +
+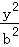 =1,将M(1,
=1,将M(1,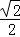 )代入,得b2=1,a2=2,
)代入,得b2=1,a2=2,
则所求椭圆方程为 +y2=1.
+y2=1.
(2)证明:因为直线l与圆x2+y2=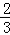 相切,
相切,
所以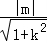 =
=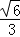 ,即m2=
,即m2=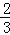 (1+k2),
(1+k2),
由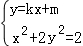 ,得(1+2k2)x2+4kmx+2m2﹣2=0.
,得(1+2k2)x2+4kmx+2m2﹣2=0.
设点A、B的坐标分别为A(x1,y1)、B(x2,y2),
则x1+x2=﹣ ,x1x2=
,x1x2=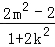 ,
,
所以y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=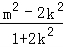 ,
,
所以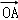 •
•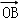 =x1x2+y1y2=
=x1x2+y1y2=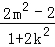 +
+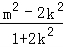 =
= =0,
=0,
故OA⊥OB.
【点评】本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,联立直线方程,运用韦达定理,同时考查直线和圆相切的条件,属于中档题.
在平面直角坐标系xOy中,直线L与抛物线y2=4x相交于不同的A、B两点.且 •
• =﹣4.
=﹣4.
(1)证明直线L必过一定点,并求出该定点.
(2)求线段AB的中点P的轨迹方程.
(3)求三角形AOB面积最小时,直线AB的方程.
知识点:3.抛物线
【考点】抛物线的简单性质.
【专题】综合题;转化思想;综合法;圆锥曲线的定义、性质与方程.
【分析】(1)设出直线的方程,同抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系表示出数量积,根据数量积等于﹣4,做出数量积表示式中的b的值,即得到定点的坐标.
(2)假设线段中点坐标,利用中点坐标公式,寻找坐标之间的关系即可求得.
(3)求出AB,原点到直线l的距离,可得面积,即可求出三角形AOB面积最小时,直线AB的方程.
【解答】(1)证明:设l:x=ty+b,代入抛物线方程y2=4x中得,y2﹣4ty﹣4b=0,
设A(x1,y1),B(x2,y2),则y1+y2=4t,y1y2=﹣4b,…
∴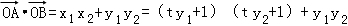
=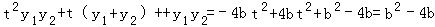 ,
,
令b2﹣4b=﹣4,∴b2﹣4b+4=0,b=2,
∴直线l过定点(2,0),∴若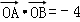 ,则直线l必过一定点…
,则直线l必过一定点…
(2)解:设P(x,y)由(1)得:y1+y2=4t,y1y2=﹣4bb=2
得x1+x2=4t2+4,∴x=2t2+2,y=2t
消去t得P点的轨迹方程为:y2=2x﹣2…
(3)解:AB= ,原点到直线l的距离
,原点到直线l的距离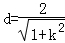 (式子中k为t)
(式子中k为t)
∴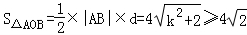
当k=0时,三角形AOB面的最小,最小值是 ….
….
【点评】本题主要考查向量的数量积的运算,考查轨迹方程的求解,利用了代入法,属于中档题.