已知复数 是纯虚数,则实数a=( )
是纯虚数,则实数a=( )
A.﹣2 B.4 C.﹣6 D.6
知识点:1.数系的扩充和复数的概念
D
【考点】复数代数形式的混合运算.
【分析】化简复数,由纯虚数的定义可得关于a的式子,解之可得.
【解答】解:化简可得复数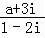 =
=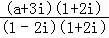 =
=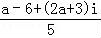 ,
,
由纯虚数的定义可得a﹣6=0,2a+3≠0,
解得a=6
故选:D
若全集U=R,集合M={x|x2>4},N={x| >0},则M∩(∁UN)等于( )
>0},则M∩(∁UN)等于( )
A.{x|x<﹣2} B.{x|x<﹣2}或x≥3} C.{x|x≥32} D.{x|﹣2≤x<3}
知识点:3.集合的基本运算
B
【考点】交、并、补集的混合运算.
【分析】分别求出M与N中不等式的解集,根据全集U=R求出N的补集,找出M与N补集的交集即可.
【解答】解:由M中的不等式解得:x>2或x<﹣2,即M={x|x<﹣2或x>2},
由N中的不等式变形得:(x﹣3)(x+1)<0,
解得:﹣1<x<3,即N={x|﹣1<x<3},
∵全集U=R,
∴∁UN={x|x≤﹣1或x≥3}
则M∩(∁UN)={x|x<﹣2或x≥3}.
故选:B.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )

A.30( +1)m B.120(
+1)m B.120( -1) m C.180(
-1) m C.180( -1)m D.240(
-1)m D.240( -1)m
-1)m
知识点:9.正弦定理和余弦定理(解三角形)
B
【考点】解三角形的实际应用.
【分析】由题意画出图形,由两角差的正切求出15°的正切值,然后通过求解两个直角三角形得到DC和DB的长度,作差后可得答案.
【解答】解:如图,∠DAB=15°,
∵tan15°=tan(45°﹣30°)=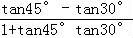 =2﹣
=2﹣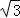 .
.
在Rt△ADB中,又AD=60,
∴DB=AD•tan15°=60×(2﹣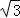 )=120﹣60
)=120﹣60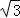 .
.
在Rt△ADC中,∠DAC=60°,AD=60,
∴DC=AD•tan60°=60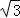 .
.
∴BC=DC﹣DB=60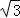 ﹣=120(
﹣=120(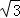 ﹣1)(m).
﹣1)(m).
∴河流的宽度BC等于120(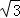 ﹣1)m.
﹣1)m.
故选:B.

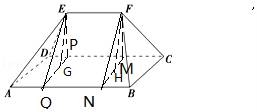
《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”意思为:“今有底面为矩形的屋脊形状的多面体(如图)”,下底面宽AD=3丈,长AB=4丈,上棱EF=2丈,EF∥平面ABCD.EF与平面ABCD的距离为1丈,问它的体积是( )

A.4立方丈 B.5立方丈 C.6立方丈 D.8立方丈
知识点:3.空间几何体的表面积与体积
B
【考点】棱柱、棱锥、棱台的体积.
【分析】过E作EG⊥平面ABCD,垂足为G,过F作FH⊥平面ABCD,垂足为H,过G作PQ∥AD,交AB于Q,交CD于P,过H信MN∥BC,交AB于N,交CD于M,则它的体积V=VE﹣AQPD+VEPQ﹣FMN+VF﹣NBCM,由此能求出结果.
【解答】解:过E作EG⊥平面ABCD,垂足为G,过F作FH⊥平面ABCD,垂足为H,
过G作PQ∥AD,交AB于Q,交CD于P,过H信MN∥BC,交AB于N,交CD于M,
则它的体积:
V=VE﹣AQPD+VEPQ﹣FMN+VF﹣NBCM
= +S△EPQ•NQ+
+S△EPQ•NQ+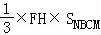
= +
+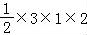 +
+
=5(立方丈).
故选:B.
直线x﹣y+m=0与圆x2+y2=1相交的一个充分不必要条件是( )
A.0<m<1 B.﹣4<m<2 C.m<1 D.﹣3<m<1
知识点:5.充分条件与必要条件
A
【考点】直线与圆的位置关系.
【分析】把直线与圆的方程联立,消去y得到一个关于x的一元二次方程,根据直线与圆有两个不同的交点得到此方程有两个不等的实根,即△>0,列出关于m的不等式,求出不等式的解集得到m的范围,在四个选项中找出解集的一个真子集即为满足题意的充分不必要条件.
【解答】解:联立直线与圆的方程,消去y得:2x2+2mx+m2﹣1=0,
由题意得:△=(2m)2﹣8(m2﹣1)=﹣4m2+8>0,
解得:﹣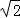 <m<
<m<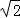 ,
,
∵0<m<1是﹣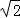 <m<
<m<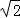 的一个真子集,
的一个真子集,
∴直线x﹣y+m=0与圆x2+y2=1相交的一个充分不必要条件是0<m<1.
故选A.
已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,a=3,则△ABC 的周长的最大值为( )
A.2 B.6 C.
B.6 C. D.9
D.9
知识点:9.正弦定理和余弦定理(解三角形)
D
【考点】余弦定理;正弦定理.
【分析】由已知利用余弦定理可求A,利用a=3和sinA的值,根据正弦定理表示出b和c,代入三角形的周长a+b+c中,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域即可得到周长的最大值.
【解答】解:∵a2=b2+c2﹣bc,可得:bc=b2+c2﹣a2,
∴cosA=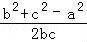 =
=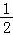 ,
,
∵A∈(0,π),
∴A=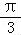 ,
,
∴由a=3,结合正弦定理得: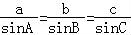 =
=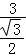 =2
=2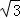 ,
,
∴b=2 sinB,c=2
sinB,c=2 sinC,
sinC,
则a+b+c=3+2 sinB+2
sinB+2 sinC
sinC
=3+2 sinB+2
sinB+2 sin(
sin(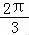 ﹣B)
﹣B)
=3+3 sinB+3cosB
sinB+3cosB
=3+6sin(B+ ),
),
可知周长的最大值为9.
故选:D.
已知数列{an}满足 (n∈N*),则 a10=( )
(n∈N*),则 a10=( )
A.e30 B. C.
C. D.e40
D.e40
知识点:7.数列的通项
B
【考点】数列的概念及简单表示法.
【分析】利用作差法求出lnan= ,n≥2,进行求解即可
,n≥2,进行求解即可
【解答】解:∵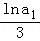 •
•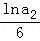 •
•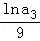 •…•
•…•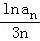 =
=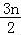 (n∈N*),
(n∈N*),
∴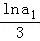 •
•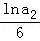 •
•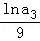 •…•
•…•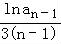 =
=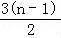 (n∈N*),
(n∈N*),
∴lnan=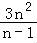 ,n≥2,
,n≥2,
∴an=e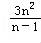 ,
,
∴a10=e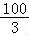 ,
,
故选B.
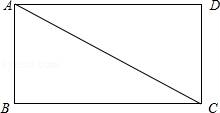
在矩形ABCD中,|AB|=3,|AC|=5, ,
, ,若
,若 =x
=x +y
+y ,则x+y的值为( )
,则x+y的值为( )
A.2 B.4 C.5 D.7
知识点:3.平面向量的基本定理及其坐标表示
D
【考点】平面向量的基本定理及其意义.
【分析】由已知利用勾股定理可得|AD|,从而可得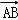 =3
=3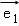 ,
,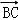 =
=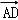 =4
=4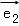 ,由向量的加法可得
,由向量的加法可得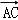 =
=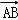 +
+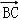 =3
=3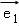 +4
+4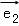 ,利用平面向量的基本定理及其意义即可得解x,y的值,进而得解.
,利用平面向量的基本定理及其意义即可得解x,y的值,进而得解.
【解答】解:∵在矩形ABCD中,|AB|=3,|AC|=5,
∴利用勾股定理可得:|AD|=4,
∵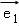 =
=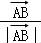 ,
,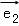 =
=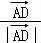 ,
,
∴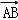 =3
=3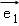 ,
,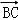 =
=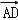 =4
=4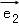 ,
,
∴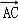 =
=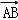 +
+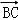 =3
=3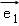 +4
+4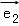 ,
,
∴x=3,y=4,可得:x+y=7.
故选:D.
函数y=xsinx+cosx的图象大致是( )
A. B.
B. C.
C. D.
D.
知识点:15.函数的图像
A
【考点】函数的图象.
【分析】利用函数的奇偶性、单调性、特殊值,借助排除法能求出结果.
【解答】解:∵y=xsinx+cosx,
设f(x)=xsinx+cosx,
则f(﹣x)=(﹣x)sin(﹣x)+cos(﹣x)=xsinx+cosx=f(x),
∴y=xsinx+cosx是偶函数,故排除D.
当x=0时,y=0+cos0=1,故排除C和D;
∵y′=xcosx,
∴x>0开始时,函数是增函数,由此排除B.
故选:A.
函数y= lnx+x-
lnx+x- -2的零点所在的区间是( )
-2的零点所在的区间是( )
A.( ,1)B.(1,2) C.(2,e) D.(e,3)
,1)B.(1,2) C.(2,e) D.(e,3)
知识点:13.函数与方程
C
【考点】函数零点的判定定理.
【分析】先判断函数y是定义域上的增函数,再利用根的存在性定理,即可得出结论.
【解答】解:∵函数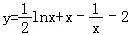 (x>0),
(x>0),
∴y′=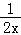 +1+
+1+ >0,
>0,
∴函数y=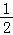 lnx+x﹣
lnx+x﹣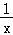 ﹣2在定义域(0,+∞)上是单调增函数;
﹣2在定义域(0,+∞)上是单调增函数;
又x=2时,y=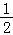 ln2+2﹣
ln2+2﹣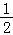 ﹣2=
﹣2=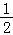 ln2﹣
ln2﹣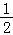 <0,
<0,
x=e时,y=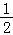 lne+e﹣
lne+e﹣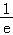 ﹣2=
﹣2=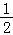 +e﹣
+e﹣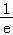 ﹣2>0,
﹣2>0,
因此函数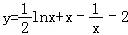 的零点在(2,e)内.
的零点在(2,e)内.
故选:C.
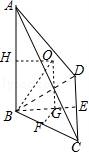
四面体ABCD的四个顶点都在球O的球面上,AB=2,BC=CD=1,∠BCD=60°,AB⊥平面BCD,则球O的表面积为( )
A.8π B. π C.
π C. π D.
π D. π
π
知识点:3.空间几何体的表面积与体积
D
【考点】球的体积和表面积.
【分析】由题意画出图形,设出底面三角形的外心G,找出四面体ABCD的外接球的球心O,通过求解直角三角形得到三棱锥的高,则答案可求.
【解答】解:如图,∵BC=CD=1,∠BCD=60°,
∴底面△BCD为等边三角形,
取CD中点为E,连接BE,
∴△BCD的外心G在BE上,设为G,取BC中点F,连接GF,
在Rt△BCE中,由CE=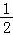 ,∠CBE=30°,得BF=
,∠CBE=30°,得BF= =
=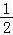 ,
,
又在Rt△BFG中,得BG=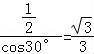 ,
,
过G作AB的平行线与AB的中垂线HO交于O,
则O为四面体ABCD的外接球的球心,即R=OB,
∵AB⊥平面BCD,∴OG⊥BG,
在Rt△BGO中,求得OB=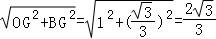 ,
,
∴球O的表面积为 .
.
故选:D.
已知如图所示的正方体ABCD﹣A1B1C1D1,点P、Q分别在棱BB1、DD1上,且, 过点A、P、Q作截面截去该正方体的含点A1的部分,则下列图形中不可能是截去后剩下几何体的主视图的是( )
过点A、P、Q作截面截去该正方体的含点A1的部分,则下列图形中不可能是截去后剩下几何体的主视图的是( )

A. B.
B. C.
C. D.
D.
知识点:2.空间几何体的三视图和直观图
A
【考点】简单空间图形的三视图.
【分析】根据剩余几何体的直观图即可得到该几何体的主视图.
【解答】解:过点A,P,Q的平面截去该正方体的上半部分后,剩余部分的直观图如图:
①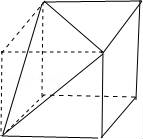 ,它的主视图是B选项中的图;
,它的主视图是B选项中的图;
②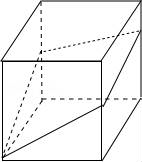 ,它的主视图是C选项中的图;
,它的主视图是C选项中的图;
③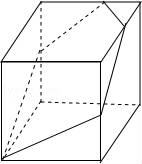 ,它的主视图是D选项中的图;
,它的主视图是D选项中的图;
∴该几何体的主视图不可能是A.
故选:A.
若曲线f(x)=3x+ax3在点(1,a+3)处的切线与直线y=6x平行,则a= .
知识点:1.变化率与导数
1
【考点】利用导数研究曲线上某点切线方程.
【分析】求出f(x)的导数,求出切线的斜率,由两直线平行的条件:斜率相等,解方程可得a=1.
【解答】解:f(x)=3x+ax3的导数为f′(x)=3+3ax2,
即有在点(1,a+3)处的切线斜率为k=3+3a,
由切线与直线y=6x平行,可得3+3a=6,
解得a=1.
故答案为:1.
记等差数列{an} 的前n项和Sn,利用倒序求和的方法得:Sn= ;类似的,记等比数列{bn}的前n项的积为Tn,且bn>0(n∈N+),试类比等差数列求和的方法,可将Tn表示成首项b1,末项bn与项数n的一个关系式,即公式Tn= .
;类似的,记等比数列{bn}的前n项的积为Tn,且bn>0(n∈N+),试类比等差数列求和的方法,可将Tn表示成首项b1,末项bn与项数n的一个关系式,即公式Tn= .
知识点:1.合情推理与演绎推理
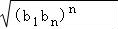
【考点】进行简单的合情推理;等比数列;等比数列的前n项和;类比推理.
【分析】由等差和等比数列的通项和求和公式及类比推理思想可得结果,在运用类比推理时,通常等差数列中的求和类比等比数列中的乘积.
【解答】解:在等差数列{an}的前n项和为Sn=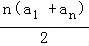 ,
,
因为等差数列中的求和类比等比数列中的乘积,
所以各项均为正的等比数列{bn}的前n项积Tn=(b1bn) 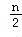
故答案为: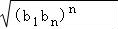 .
.
已知cos( ﹣α)=
﹣α)= ,则sin(
,则sin( ﹣2α)= .
﹣2α)= .
知识点:4.和角公式与倍(半)角公式
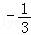
【考点】两角和与差的正弦函数.
【分析】由条件利用诱导公式、二倍角公式,求得sin( ﹣2α)=sin[2(
﹣2α)=sin[2(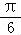 ﹣α)+
﹣α)+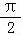 ]的值.
]的值.
【解答】解:∵已知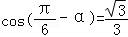 ,则sin(
,则sin(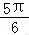 ﹣2α)=sin[2(
﹣2α)=sin[2(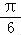 ﹣α)+
﹣α)+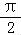 ]=cos2(
]=cos2(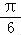 ﹣α)=2cos2(
﹣α)=2cos2(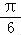 ﹣α)﹣1=2•
﹣α)﹣1=2• ﹣1=﹣
﹣1=﹣ ,
,
故答案为: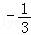 .
.
已知实数x,y满足不等式组  ,则z=|x|+y的取值范围为 .
,则z=|x|+y的取值范围为 .
知识点:3.二元一次不等式(组)与简单的线性规划
[﹣1,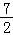 ]
]
【考点】简单线性规划.
【分析】先画出满足条件的平面区域,通过讨论x的范围,求出直线的表达式,结合图象从而求出z的范围.
【解答】解:画出满足条件的平面区域,如图示:
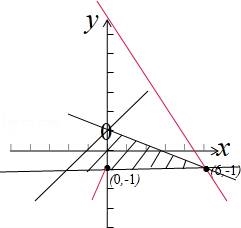 ,
,
z=|x|+y=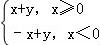 ,
,
当M(x,y)位于D中y轴的右侧包括y轴时,平移直线:x+y=0,可得x+y∈[﹣1,2],
当M(x,y)位于D中y轴左侧,平移直线﹣x+y=0,可得z=﹣x+y∈(﹣1,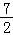 ].
].
所以z=|x|+y的取值范围为:[﹣1,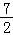 ].
].
故答案为:[﹣1,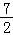 ].
].
已知 =(bsinx,acosx),
=(bsinx,acosx), =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= •
• +a,其中a,b,x∈R.且满足f(
+a,其中a,b,x∈R.且满足f( )=2,f′(0)=2
)=2,f′(0)=2 .
.
(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)﹣ =0在区间[0,
=0在区间[0, ]上总有实数解,求实数k的取值范围.
]上总有实数解,求实数k的取值范围.
知识点:4.平面向量的数量积(夹角、模)
【考点】平面向量数量积的运算;三角函数中的恒等变换应用.
【分析】(I)利用数量积运算和导数的运算法则即可得出;
(II)利用两角和差的正弦公式、正弦函数的单调性有界性、对数的运算法则即可得出.
【解答】解:(Ⅰ)由题意知,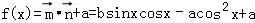 =
=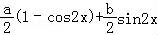 ,
,
由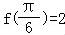 得
得 ,
,
∵f′(x)=asin2x+bcos2x,又 ,∴
,∴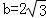 ,∴a=2.
,∴a=2.
(Ⅱ)由(Ⅰ)得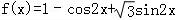 =
=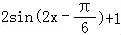 ,
,
∵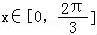 ,
, ,
,
∴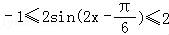 ,f(x)∈[0,3].
,f(x)∈[0,3].
又∵ 有解,即f(x)=﹣log3k有解,
有解,即f(x)=﹣log3k有解,
∴﹣3≤log3k≤0,解得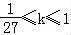 ,
,
∴实数k的取值范围为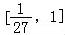 .
.
如图:在△ABC中,D为AB边上一点,DA=DC,已知∠B= ,BC=3
,BC=3
(1)若△BCD为锐角三角形,DC= ,求角A的大小;
,求角A的大小;
(2)若△BCD的面积为 ,求边AB的长.
,求边AB的长.

知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;正弦定理.
【分析】(1)由已知及正弦定理可求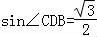 ,结合△BCD为锐角三角形,可求∠CDB,进而可求∠ADC的值,又DA=DC,利用等腰三角形的性质即可得解∠A的值.
,结合△BCD为锐角三角形,可求∠CDB,进而可求∠ADC的值,又DA=DC,利用等腰三角形的性质即可得解∠A的值.
(2)利用三角形面积公式可求BD的值,利用余弦定理可求得CD的值,进而可求AB=CD+BD的值.
【解答】(本题满分为12分)
解:(1)因为:在△BCD中,由正弦定理得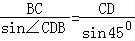 ,
,
所以: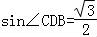 ,
,
又因为:△BCD为锐角三角形,
所以:∠CDB=60°,
所以:∠ADC=120°,DA=DC,
所以:∠A=∠ACD=30°,∠A=30°.…
(2)因为: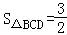 ,
,
所以: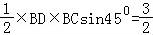 ,
,
所以: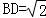 ,
,
在△BCD中由余弦定理得:CD2=BD2+BC2﹣2BD×BCcos∠B=2+9﹣6=5,
所以: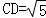 ,
,
所以: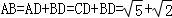 .…
.…
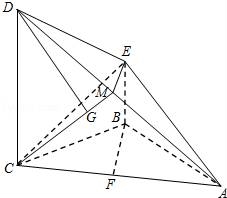
如图,四棱锥A﹣BCDE中,CD⊥平面ABC,BE∥CD,AB=BC=CD,AB⊥BC,M为AD上一点,EM⊥平面ACD.
(Ⅰ)求证:EM∥平面ABC.
(Ⅱ)若CD=2BE=2,求点D到平面EMC的距离.

知识点:10.空间角与距离
【考点】点、线、面间的距离计算;直线与平面平行的判定.
【分析】(Ⅰ)取AC的中点F,连接BF,证明BF⊥平面ACD,结合EM⊥平面ACD,所以EM∥BF,再结合线面平行的判定定理得到EM∥面ABC;
(Ⅱ)由等面积法求出点D到平面EMC的距离.
【解答】证明:(Ⅰ)取AC的中点F,连接BF,
因为AB=BC,所以BF⊥AC,
又因为CD⊥平面ABC,所以CD⊥BF,
所以BF⊥平面ACD,…
因为EM⊥平面ACD,
所以EM∥BF,
因为EM⊄面ABC,BF⊂平面ABC,
所以EM∥平面ABC; …
解:(Ⅱ)因为EM⊥平面ACD,EM⊂面EMC,
所以平面CME⊥平面ACD,平面CME∩平面ACD=CM,
过点D作直线DG⊥CM,则DG⊥平面CME,…
由已知CD⊥平面ABC,BE∥CD,AB=BC=CD=2BE,可得AE=DE,
又EM⊥AD,
所以M为AD的中点,
在Rt△ABC中,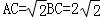 ,
,
在Rt△ADC中,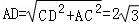 ,
,
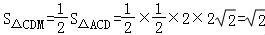 ,
,
在△DCM中, ,
,
由等面积法知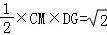 ,
,
所以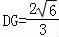 ,
,
即点D到平面EMC的距离为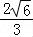 .…
.…
已知数列{an}的各项均是正数,其前n项和为Sn,满足Sn=4﹣an.
(1)求数列{an}的通项公式;
(2)设bn=  (n∈N*),求数列{bn}的前2n项和T2n.
(n∈N*),求数列{bn}的前2n项和T2n.
知识点:5.等比数列的前n项和
【考点】数列的求和;数列递推式.
【分析】(1)利用递推关系与等比数列的通项公式即可得出;
(2)n为奇数时,bn=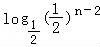 =n﹣2.n为偶数时,bn=
=n﹣2.n为偶数时,bn=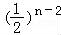 .分组分别利用等差数列与等比数列的求和公式即可得出.
.分组分别利用等差数列与等比数列的求和公式即可得出.
【解答】解:(1)由Sn=4﹣an,Sn+1=4﹣an+1,两式相减得an+1=an﹣an+1,
得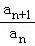 =
=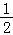 ,
,
又a1=S1=4﹣a1,解得a1=2.
故数列{an}是以2为首项,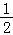 为公比的等比数列.
为公比的等比数列.
故an=2×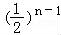 =
= .
.
(2)n为奇数时,bn=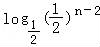 =n﹣2.
=n﹣2.
n为偶数时,bn= .
.
∴T2n=(b1+b3+…+b2n﹣1)+(b2+b4+…+b2n)
=[﹣1+1+…+(2n﹣3)]+ +…+
+…+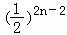
=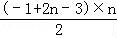 +
+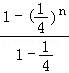
=n2﹣2n+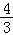
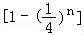 .
.
在平面直角坐标系xOy中,已知圆O的方程为x2+y2=2
(1)若直线l与圆O切于第一象限,且与坐标轴交于点D,E,当DE长最小时,求直线l的方程;
(2)设M,P是圆O上任意两点,点M关于x轴的对称点N,若直线MP,NP分别交x轴于点(m,0)(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.
知识点:4.直线与圆的位置关系
【考点】直线与圆的位置关系.
【分析】(1)设直线l的方程,利用直线l与圆O相切,及基本不等式,可求DE长最小时,直线l的方程.
(2)设M(x1,y1),P(x2,y2),则N(x1,﹣y1), =2,
=2,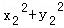 =2,求出直线MP、NP分别与x轴的交点,进而可求mn的值2
=2,求出直线MP、NP分别与x轴的交点,进而可求mn的值2
【解答】解:(1)设直线l的方程为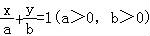 ,
,
即bx+ay﹣ab=0,
由直线l与圆O相切,得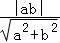 =
=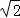 ,即
,即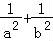 =
=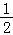 ,
,
DE2=a2+b2=2(a2+b2)(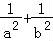 )≥8,
)≥8,
当且仅当a=b=2时取等号,
此时直线l的方程为x+y﹣2=0,
所以当DE长最小时,直线l的方程为x+y﹣2=0.
(3)设M(x1,y1),P(x2,y2),
则N(x1,﹣y1),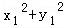 =2,
=2,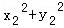 =2,
=2,
直线MP与x轴交点(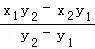 ,0),m=
,0),m=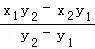 ,
,
直线NP与x轴交点( ,0),n=
,0),n=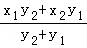 ,
,
mn=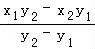 ×
×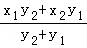 =
=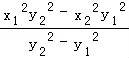 =
=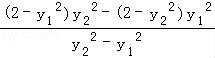 =2.
=2.
∴mn为定值2.
已知函数f(x)=x﹣ax2﹣lnx(a>0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)>3﹣2ln2.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的极值;利用导数研究函数的单调性.
【分析】(1)先求出函数的导数,通过讨论a的范围,确定导函数的符号,从而判断函数的单调性;
(2)表示出f(x1)+f(x2)=lna+ +ln2+1,通过求导进行证明.
+ln2+1,通过求导进行证明.
【解答】解:(1)∵f′(x)=﹣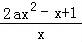 ,(x>0,a>0),
,(x>0,a>0),
不妨设φ(x)=2ax2﹣x+1(x>0,a>0),
则关于x的方程2ax2﹣x+1=0的判别式△=1﹣8a,
当a≥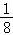 时,△≤0,φ(x)≥0,故f′(x)≤0,
时,△≤0,φ(x)≥0,故f′(x)≤0,
∴函数f(x)在(0,+∞)上单调递减,
当0<a<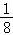 时,△>0,方程f′(x)=0有两个不相等的正根x1,x2,
时,△>0,方程f′(x)=0有两个不相等的正根x1,x2,
不妨设x1<x2,则当x∈(0,x1)及x∈(x2,+∞)时f′(x)<0,
当x∈(x1,x2)时,f′(x)>0,
∴f(x)在(0,x1),(x2,+∞)递减,在(x1,x2)递增;
(2)由(1)知当且仅当a∈(0,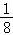 )时f(x)有极小值x1 和极大值x2,
)时f(x)有极小值x1 和极大值x2,
且x1,x2是方程的两个正根,则x1+x2=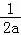 ,x1 x2=
,x1 x2=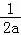 ,
,
∴f(x1)+f(x2)=(x1+x2)﹣a[(x1+x2)2﹣2x1 x2]﹣(lnx1+lnx2)
=ln(2a)+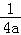 +1=lna+
+1=lna+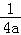 +ln2+1(0<a<
+ln2+1(0<a<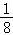 ),
),
令g(a)=lna+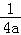 +ln2+1,
+ln2+1,
当a∈(0,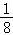 )时,g′(a)=
)时,g′(a)=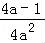 <0,
<0,
∴g(a)在(0,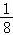 )内单调递减,
)内单调递减,
故g(a)>g(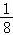 )=3﹣2ln2,
)=3﹣2ln2,
∴f(x1)+f(x2)>3﹣2ln2.