已知数列 ,那么9是此数列的第( )项.
,那么9是此数列的第( )项.
A.12 B.13 C.14 D.15
知识点:1.数列的概念与表示方法
C
【考点】数列的概念及简单表示法.
【分析】根据题意,分析可得数列的通项公式为an=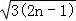 ,令an=
,令an=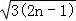 =9,解可得n的值,即可得答案.
=9,解可得n的值,即可得答案.
【解答】解:根据题意,数列 ,
,
则有an=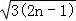 ,
,
若an=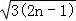 =9,解可得n=14,
=9,解可得n=14,
即9是此数列的第14项,
故选:C.
下列通项公式可以作为等比数列通项公式的是( )
A.an=2n B. C.
C. D.an=log2n
D.an=log2n
知识点:4.等比数列及其性质
C
【考点】等比数列的通项公式.
【分析】利用等比数列定义求解.
【解答】解:在A中,an=2n,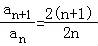 =
=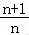 ,不是常数,故A不成立;
,不是常数,故A不成立;
在B中, ,
,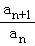 =
=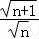 ,不是常数,故B不成立;
,不是常数,故B不成立;
在C中,an=2﹣n,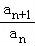 =
= =
=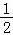 ,是常数,故C成立;
,是常数,故C成立;
在D中,an=log2n,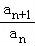 =
=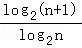 ,不是常数,故D不成立.
,不是常数,故D不成立.
故选:C.
下列命题中,一定正确的是( )
A.若 ,则a>0,b<0 B.若a>b,b≠0,则
,则a>0,b<0 B.若a>b,b≠0,则
C.若a>b,a+c>b+d,则c>d D.若a>b,c>d,则ac>bd
知识点:1.不等式关系与不等式
A
【考点】不等式的基本性质.
【分析】A.由a>b,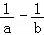 =
=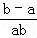 >0,可得ab<0,因此a>0>b,即可判断出正误.
>0,可得ab<0,因此a>0>b,即可判断出正误.
B.b<0时不成立.
C.取a=6,b=1,c=1,d=2,即可判断出正误.
D.取a=5,b=﹣3,c=1,d=﹣6,即可判断出正误.
【解答】解:A.∵a>b,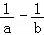 =
=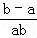 >0,∴ab<0,因此a>0>b,正确.
>0,∴ab<0,因此a>0>b,正确.
B.b<0时不成立.
C.取a=6,b=1,c=1,d=2,满足a>b,a+c>b+d,而c<d,因此不正确.
D.取a=5,b=﹣3,c=1,d=﹣6,满足a>b,c>d,则ac<bd,不正确.
故选:A.
等差数列{an}中,已知a1﹣a4﹣a8﹣a12+a15=2,则此数列的前15项和S15等于( )
A.﹣30 B.15 C.﹣60 D.﹣15
知识点:3.等差数列的前n项和
A
【考点】等差数列的前n项和.
【分析】根据题意和等差数列的性质化简已知的等式,由等差数列的前n项和公式、等差数列的性质求出S15的值.
【解答】解:∵a1﹣a4﹣a8﹣a12+a15=2,
∴a1﹣(a4+a8+a12)+a15=2,则2a8﹣3a8=2,
解得a8=﹣2,
∴S15=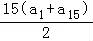 =15a8=﹣30,
=15a8=﹣30,
故选:A.
在△ABC,已知acosA=bcosB,则△ABC的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
知识点:9.正弦定理和余弦定理(解三角形)
D
【考点】正弦定理.
【分析】根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°答案可得.
【解答】解:根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴A=B,或2A+2B=180°即A+B=90°,
所以△ABC为等腰或直角三角形.
故选:D.
若lg2,lg(2x﹣1),lg(2x+3)成等差数列,则x的值等于( )
A.1 B.0或32 C.32 D.log25
知识点:2.等差数列及其性质
D
【考点】等差数列的性质.
【分析】根据题意,可得lg2+lg(2x+3)=2lg(2x﹣1),由对数的运算性质可得lg[2•(2x+3)]=lg(2x﹣1)2,解可得2x的值,由指数的运算性质可得答案.
【解答】解:若lg2,lg(2x﹣1),lg(2x+3)成等差数列,则lg2+lg(2x+3)=2lg(2x﹣1),
由对数的运算性质可得lg[2•(2x+3)]=lg(2x﹣1)2,
解得2x=5或2x=﹣1(不符合指数函数的性质,舍去)
则x=log25
故选D.
等比数列{an}前n项和Sn中,S4=1,S8=3,则a17+a18+a19+a20=( )
A.20 B.14 C.16 D.18
知识点:5.等比数列的前n项和
C
【考点】等比数列的前n项和.
【分析】设等比数列{an}的公比是q,由题意和等比数列的前n项和列出方程组,由等比数列的通项公式化简后求出q的值,再表示所求的式子求出答案.
【解答】解:设等比数列{an}的公比是q,
∵S4=1,S8=3,
∴ ,两式相除得q4=2,
,两式相除得q4=2,
∴a17+a18+a19+a20=(a1+a2+a3+a4)q16=16,
故选C.
下列正确的是( )
A.若a,b∈R,则 B.若x<0,则x+
B.若x<0,则x+ ≥﹣2
≥﹣2 =﹣4
=﹣4
C.若ab≠0,则 D.若x<0,则2x+2﹣x>2
D.若x<0,则2x+2﹣x>2
知识点:4.基本不等式
D
【考点】基本不等式.
【分析】利用基本不等式的使用法则“一正二定三相等”即可判断出正误.
【解答】解:A.ab<0时不成立.
B.x<0,则x+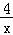 =﹣
=﹣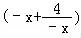 ≤﹣2
≤﹣2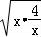 =﹣4,因此不成立.
=﹣4,因此不成立.
C.取a=﹣1,b=﹣2时,不成立.
D.x<0,则2x+2﹣x>2,成立.
故选:D.
设变量x、y满足约束条件 ,则目标函数z=2x+y的最小值为( )
,则目标函数z=2x+y的最小值为( )
A.2 B.3 C.4 D.9
知识点:3.二元一次不等式(组)与简单的线性规划
B
【考点】简单线性规划的应用.
【分析】本题主要考查线性规划的基本知识,先画出约束条件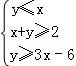 的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数Z=2x+y的最小值.
的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数Z=2x+y的最小值.
【解答】解:设变量x、y满足约束条件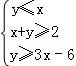 ,
,
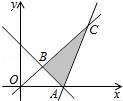
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),
则目标函数z=2x+y的最小值为3,
故选B
已知等比数列a1,a2,…a8各项为正且公比q≠1,则( )
A.a1+a8=a4+a5
B.a1+a8<a4+a5
C.a1+a8>a4+a5
D.a1+a8与a4+a5大小关系不能确定
知识点:4.等比数列及其性质
C
【考点】等比数列的通项公式.
【分析】把数列的各项用首项和公比表示,然后直接作差得答案.
【解答】解:由题意可知,a1>0,q>0,
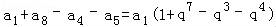 =
=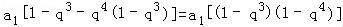 >0.
>0.
∴a1+a8>a4+a5.
故选:C.
若关于x的方程9x+(a+4)•3x+4=0有实数解,则实数a的取值范围是( )
A.(﹣∞,﹣8]∪[0,+∞) B.(﹣∞,﹣4) C.[﹣8,﹣4) D.(﹣∞,﹣8]
知识点:13.函数与方程
D
【考点】根的存在性及根的个数判断.
【分析】令3x=t>0,由条件可得a=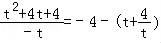 ,利用基本不等式和不等式的性质求得实数a的取值范围.
,利用基本不等式和不等式的性质求得实数a的取值范围.
【解答】解:令3x=t>0,则关于x的方程9x+(4+a)•3x+4=0 即 t2+(4+a)t+4=0 有正实数解.
故a=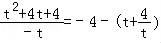 ,
,
由基本不等式可得:t+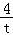 ≥4,当且仅当t=
≥4,当且仅当t=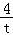 时,等号成立,
时,等号成立,
∴﹣(t+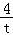 )≤﹣4,即﹣4﹣(t+
)≤﹣4,即﹣4﹣(t+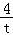 )≤﹣8,
)≤﹣8,
∴a≤﹣8,
∴a的取值范围是(﹣∞,﹣8].
故选:D.
定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①② B.③④ C.①③ D.②④
知识点:4.等比数列及其性质
C
【考点】等比关系的确定.
【分析】根据新定义,结合等比数列性质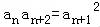 ,一一加以判断,即可得到结论.
,一一加以判断,即可得到结论.
【解答】解:由等比数列性质知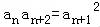 ,
,
① =f2(an+1),故正确;
=f2(an+1),故正确;
②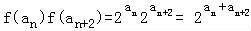 ≠
≠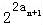 =f2(an+1),故不正确;
=f2(an+1),故不正确;
③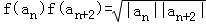 =
=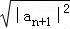 =f2(an+1),故正确;
=f2(an+1),故正确;
④f(an)f(an+2)=ln|an|ln|an+2|≠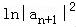 =f2(an+1),故不正确;
=f2(an+1),故不正确;
故选C
设 ,则a,b的大小关系为 .
,则a,b的大小关系为 .
知识点:1.不等式关系与不等式
a<b
【考点】不等式比较大小.
【分析】作差利用分母有理化因式即可得出.
【解答】解:b﹣a=﹣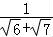 +
+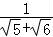 >0,
>0,
∴b>a.
故答案为:a<b.
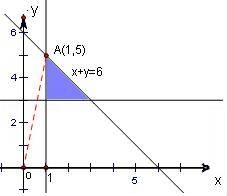
若x,y满足 ,则
,则 的最大值为 .
的最大值为 .
知识点:3.二元一次不等式(组)与简单的线性规划
5
【考点】简单线性规划.
【分析】本题主要考查线性规划的基本知识,先画出约束条件 ,的可行域,然后分析
,的可行域,然后分析 的几何意义,结合图象,用数形结合的思想,即可求解.
的几何意义,结合图象,用数形结合的思想,即可求解.
【解答】解:满足约束条件 的可行域:
的可行域:
如下图所示:
又∵ 的表示的是可行域内一点与原点连线的斜率
的表示的是可行域内一点与原点连线的斜率
当x=1,y=5时, 有最大值5.
有最大值5.
给答案为:5.
若关于x的不等式(m﹣1)x2﹣mx+m﹣1>0的解集为空集,则实数m的取值为 .
知识点:2.一元二次不等式及不等式的解法
m≤
【考点】一元二次不等式的解法.
【分析】关于x的不等式(m﹣1)x2﹣mx+m﹣1>0的解集为∅,可转化成不等式(m﹣1)x2﹣mx+m﹣1≤0恒成立,然后讨论二次项系数和判别式可得结论.
【解答】解:∵关于x的不等式(m﹣1)x2﹣mx+m﹣1>0的解集为∅,
∴不等式(m﹣1)x2﹣mx+m﹣1≤0恒成立
①当m﹣1=0时,(m﹣1)x2﹣mx+m﹣1≤0,即x≥0,不是对任意x∈R恒成立;
②当m﹣1≠0时,∀x∈R,使(m﹣1)x2﹣mx+m﹣1≤0,
即m﹣1<0且△=(﹣m)2﹣4(m﹣1)(m﹣1)≤0,
解得m≤
综上,实数m的取值范围是m≤ .
.
故答案为m≤ .
.
已知 ,则a+b的最小值为 .
,则a+b的最小值为 .
知识点:4.基本不等式
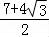
【考点】对数的运算性质.
【分析】由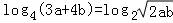 ,可得3a+4b=
,可得3a+4b=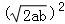 =2ab,a,b>0.
=2ab,a,b>0.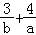 =2,再利用“乘1法”与基本不等式的性质即可得出.
=2,再利用“乘1法”与基本不等式的性质即可得出.
【解答】解:∵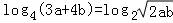 ,∴3a+4b=
,∴3a+4b=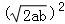 =2ab,a,b>0.
=2ab,a,b>0.
∴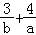 =2,∴a+b=
=2,∴a+b=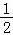 (a+b)
(a+b)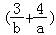 =
=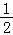 (7+
(7+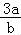 +
+ )≥
)≥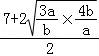 =
= ,
,
当且仅当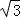 a=2b=3+2
a=2b=3+2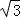 .
.
则a+b的最小值为 ,
,
故答案为: .
.
解不等式:
(1) ≥0
≥0
(2) >1.
>1.
知识点:2.一元二次不等式及不等式的解法
【考点】其他不等式的解法.
【分析】(1)将分式不等式等价转化后,由一元二次不等式的解法求出解集;
(2)将分式不等式右边化零、并因式分解后,进行等价转化,由穿根法求出不等式的解集.
【解答】解:(1)由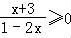 得
得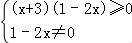 ,
,
则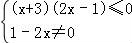 ,解得﹣3≤x<
,解得﹣3≤x< ,
,
所以不等式的解集是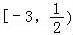 ;
;
(2)由 得
得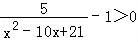 ,
,
化简得 ,即
,即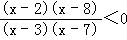 ,
,
等价于(x﹣2)(x﹣8)(x﹣3)(x﹣7)<0,如图所示:
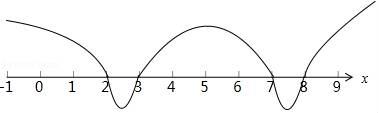
由图可得,不等式的解集是(2,3)∪(7,8).
已知三角形的三内角A、B、C所对边的长分别为a、b、c,设向量 ,
, ,若
,若 .
.
(1)求角B的大小;
(2)若△ABC的面积为 ,求AC边的最小值,并指明此时三角形的形状.
,求AC边的最小值,并指明此时三角形的形状.
知识点:4.平面向量的数量积(夹角、模)
【考点】余弦定理;三角形的形状判断;正弦定理.
【分析】(1)利用两个向量共线的性质、正弦定理可得2sinAcosB=sin(B+C)=sinA,由sinA>0,求得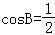 ,从而求得B的值.
,从而求得B的值.
(2)由△ABC的面积为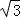 ,求得ac=4,再利用余弦定理以及基本不等式求出AC的最小值.
,求得ac=4,再利用余弦定理以及基本不等式求出AC的最小值.
【解答】解:(1)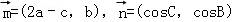 ,∵
,∵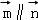 ,∴(2a﹣c)cosB=bcosC.
,∴(2a﹣c)cosB=bcosC.
由正弦定理得:(2sinA﹣sinC)cosB=sinBcosC,
整理得:2sinAcosB=sinCcosB+sinBcosC,
即2sinAcosB=sin(B+C)=sinA,∵sinA>0,∴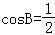 .
.
∵0<B<π,∴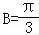 . …
. …
(2)由已知得: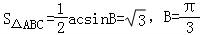 ,∴ac=4.
,∴ac=4.
由余弦定理,b2=a2+c2﹣2accosB=a2+c2﹣ac≥2ac﹣ac=ac,当且仅当“a=c”时取等号.
∴AC的最小值为2,此时三角形为等边三角形.…
已知等差数列{an}的前n项和为 ,且a1与a5的等差中项为18.
,且a1与a5的等差中项为18.
(1)求{an}的通项公式;
(2)若an=2log2bn,求数列{bn}的前n项和Tn.
知识点:3.等差数列的前n项和
【考点】数列的求和;等差数列的通项公式.
【分析】(1)依题意,可求得p的值,继而可求得数列{an}的首项与公差,从而可得通项公式;
(2)由an=2log2bn可求得bn=24n﹣3,利用等比数列的求和公式可求数列{bn}的前n项和Tn.
【解答】解:(1)∵数列{an}为等差数列,
且a1与a5的等差中项为18,
∴a3=18,
又a3=S3﹣S2=(9p﹣6)﹣(4p﹣4)=5p﹣2,
∴5p﹣2=18,解得:p=4,
∴a1=S1=4﹣2=2,∴公差d=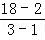 =8,
=8,
∴an=2+(n﹣1)×8=8n﹣6;
(2)∵an=2log2bn=8n﹣6,
∴bn=24n﹣3,
∴数列{bn}是以2为首项,24=16为公比的等比数列,
∴数列{bn}的前n项和Tn= =
=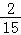 (16n﹣1).
(16n﹣1).
设函数f(x)=4x2+ax+2,不等式f(x)<c的解集为(﹣1,2).
(1)求a的值;
(2)解不等式 .
.
知识点:2.一元二次不等式及不等式的解法
【考点】其他不等式的解法;一元二次不等式的解法.
【分析】(1)利用韦达定理,建立方程,即可求a的值;
(2)不等式转化为(4x+m)(﹣4x+2)>0,分类讨论,解不等式.
【解答】解:(1)∵函数f(x)=4x2+ax+2,不等式f(x)<c的解集为(﹣1,2),
∴﹣1+2=﹣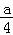 ,∴a=﹣4;
,∴a=﹣4;
(2)不等式转化为(4x+m)(﹣4x+2)>0,
可得m=﹣2,不等式的解集为∅;
m<﹣2,不等式的解集为{x|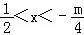 };
};
m>﹣2,不等式的解集为{x|﹣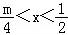 }.
}.
在△ABC中,A=30°,BC=2 ,D是AB边上的一点,CD=2,△BCD的面积为4,则AC的长为 .
,D是AB边上的一点,CD=2,△BCD的面积为4,则AC的长为 .
知识点:9.正弦定理和余弦定理(解三角形)
4或2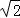
【考点】余弦定理;正弦定理.
【分析】由△BCD的面积为4,求得sin∠BCD 的值,进而求得cos∠BCD 的值,△BCD中,由余弦定理可得BD 的值,△BCD中,由正弦定理求得sinB 的值.再在△ABC中,由正弦定理求得AC的长.
【解答】解:由题意可得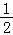 CB•CD•sin∠BCD=4,即
CB•CD•sin∠BCD=4,即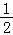 ×2
×2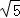 ×2 sin∠BCD=4,解得 sin∠BCD=
×2 sin∠BCD=4,解得 sin∠BCD=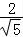 .
.
①当∠BCD 为锐角时,cos∠BCD= .
.
△BCD中,由余弦定理可得 BD=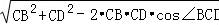 =4.
=4.
△BCD中,由正弦定理可得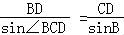 ,即
,即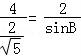 ,故 sinB=
,故 sinB=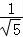 .
.
在△ABC中,由正弦定理可得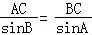 ,即
,即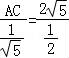 ,解得 AC=4.
,解得 AC=4.
②当∠BCD 为钝角时,cos∠BCD=﹣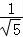 .
.
△BCD中,由余弦定理可得 BD=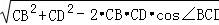 =4
=4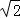 .
.
△BCD中,由正弦定理可得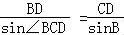 ,即
,即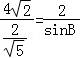 ,故 sinB=
,故 sinB= .
.
在△ABC中,由正弦定理可得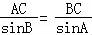 ,即
,即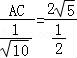 ,解得 AC=2
,解得 AC=2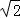 .
.
综上可得 AC=4或2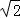 ,
,
故答案为 4或2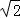 .
.
已知a1=3,an=2an﹣1+(t+1)•2n+3m+t(t,m∈R,n≥2,n∈N*)
(1)t=0,m=0时,求证: 是等差数列;
是等差数列;
(2)t=﹣1,m= 是等比数列;
是等比数列;
(3)t=0,m=1时,求数列{an}的通项公式和前n项和.
知识点:2.等差数列及其性质
【考点】数列的求和;数列递推式.
【分析】(1)两边同除以2n,由等差数列的定义,即可得证;
(2)两边同加上3,由等比数列的定义,即可得证;
(3)两边同除以2n,可得 =
=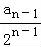 +1+
+1+ ,即为
,即为 =
=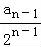 =1+
=1+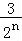 ,再由数列恒等式,可得数列{an}的通项公式;再由错位相减法和等比数列的求和公式,计算即可得到所求和.
,再由数列恒等式,可得数列{an}的通项公式;再由错位相减法和等比数列的求和公式,计算即可得到所求和.
【解答】解:(1)证明:t=0,m=0时,an=2an﹣1+2n,
两边同除以2n,可得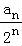 =
= +1,
+1,
即有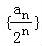 是首项为
是首项为 ,公差为1的等差数列;
,公差为1的等差数列;
(2)证明:t=﹣1,m=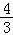 时,an=2an﹣1+3,
时,an=2an﹣1+3,
两边同加上3,可得an+3=2(an﹣1+3),
即有数列{an+3}为首项为6,公比为2的等比数列;
(3)t=0,m=1时,an=2an﹣1+2n+3,
两边同除以2n,可得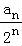 =
= +1+
+1+ ,
,
即为 =
=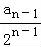 =1+
=1+ ,
,
即有得 =
=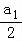 +(
+(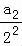 ﹣
﹣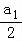 )+(
)+( ﹣
﹣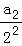 )+…+(
)+…+(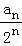 ﹣
﹣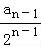 )
)
=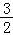 +1+
+1+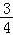 +1+
+1+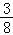 +…+1+
+…+1+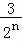 ,
,
=n﹣1+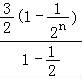 =n+2﹣
=n+2﹣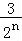 ,
,
则an=(n+2)•2n﹣3,
前n项和Sn=3•2+4•22+5•23+…+(n+2)•2n﹣3n,
可令Rn=3•2+4•22+5•23+…+(n+2)•2n,
2Rn=3•22+4•23+5•24+…+(n+2)•2n+1,
两式相减可得,﹣Rn=3•2+22+23+…+2n﹣(n+2)•2n+1
=4+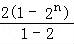 ﹣(n+2)•2n+1
﹣(n+2)•2n+1
=2﹣(n+1)•2n+1,
则Rn═(n+1)•2n+1﹣2,
Sn=(n+1)•2n+1﹣2﹣3n.