已知集合A={y|y=log2x,x>1},B={x|y= },则A∩B=( )
},则A∩B=( )
A.{y|0<y< } B.{y|0<y<1} C.{y|
} B.{y|0<y<1} C.{y| <y<1} D.∅
<y<1} D.∅
知识点:3.集合的基本运算
A
【考点】1E:交集及其运算.
【分析】求出集合的等价条件,结合交集运算进行求解即可.
【解答】解:A={y|y=log2x,x>1}={y|y>0},
B={x|y=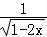 }={x|1﹣2x>0}={x|x<
}={x|1﹣2x>0}={x|x<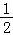 },
},
则A∩B={y|0<y<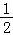 },
},
故选:A
若复数 的实部与虚部相等,则实数a的值为( )
的实部与虚部相等,则实数a的值为( )
A.3 B.﹣3 C. D.﹣
D.﹣
知识点:3.复数代数形式的四则运算
D
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数的运算法则、实部与虚部的定义即可得出.
【解答】解:复数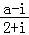 =
=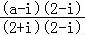 =
=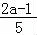 +
+ i的实部与虚部相等,
i的实部与虚部相等,
∴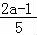 =
=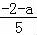 ,解得a=﹣
,解得a=﹣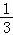 .
.
故选:D.
已知a=log0.55、b=log32、c=20.3、d=( )2,从这四个数中任取一个数m,使函数f(x)=
)2,从这四个数中任取一个数m,使函数f(x)= x3+mx2+x+2有极值点的概率为( )
x3+mx2+x+2有极值点的概率为( )
A. B.
B. C.
C. D.1
D.1
知识点:3.几何概型
B
【考点】6D:利用导数研究函数的极值;CB:古典概型及其概率计算公式.
【分析】求出函数的导数,根据函数的极值点的个数求出m的范围,通过判断a,b,c,d的范围,得到满足条件的概率值即可.
【解答】解:f′(x)=x2+2mx+1,
若函数f(x)有极值点,
则f′(x)有2个不相等的实数根,
故△=4m2﹣4>0,解得:m>1或m<﹣1,
而a=log0.55<﹣2,0<b=log32<1、c=20.3>1,0<d=(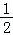 )2<1,
)2<1,
满足条件的有2个,分别是a,c,
故满足条件的概率p=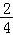 =
=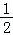 ,
,
故选:B.
如图,若N=10,则输出的数等于( )

A. B.
B. C.
C. D.
D.
知识点:1.算法与程序框图
C
【考点】EF:程序框图.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=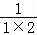 +
+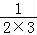 +…+
+…+ 的值,由裂项法即可计算得解.
的值,由裂项法即可计算得解.
【解答】解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是累加并输出S=S=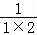 +
+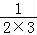 +…+
+…+ 的值,
的值,
又由:S=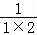 +
+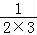 +…+
+…+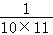 =(1﹣
=(1﹣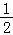 )+(
)+(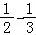 )+…+(
)+…+(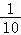 ﹣
﹣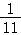 )=1﹣
)=1﹣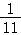 =
=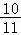 .
.
故选:C.
经过点(1, ),渐近线与圆(x﹣3)2+y2=1相切的双曲线的标准方程为( )
),渐近线与圆(x﹣3)2+y2=1相切的双曲线的标准方程为( )
A.x2﹣8y2=1 B.2x2﹣4y2=1 C.8y2﹣x2=1 D.4x2﹣2y2=1
知识点:2.双曲线
C
【考点】KB:双曲线的标准方程.
【分析】设双曲线的渐近线方程为mx±ny=0(m>0,n>0),利用渐近线与圆(x﹣3)2+y2=1相切,可得渐近线方程,设出双曲线方程,代入点(1,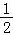 ),即可得出结论.
),即可得出结论.
【解答】解:设双曲线的渐近线方程为mx±ny=0(m>0,n>0)
∵渐近线与圆(x﹣3)2+y2=1相切,
∴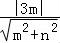 =1,
=1,
∴n=2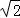 m,∴渐近线方程为x±2
m,∴渐近线方程为x±2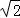 y=0
y=0
∴双曲线方程设为x2﹣8y2=λ,
代入点(1,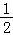 ),可得λ=1﹣2=﹣1,
),可得λ=1﹣2=﹣1,
∴双曲线方程为8y2﹣x2=1.
故选:C.
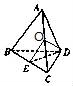
已知三棱锥A﹣BCD的各棱长都相等,E为BC中点,则异面直线AB与DE所成角的余弦值为( )

A. B.
B. C.
C. D.
D.
知识点:10.空间角与距离
B
【考点】LM:异面直线及其所成的角.
【分析】取AC中点O,连结DO,EO,则EO∥AB,从而∠DEO是异面直线AB与DE所成角(或所成角的补角),由此利用余弦定理能求出异面直线AB与DE所成角的余弦值.
【解答】解:取AC中点O,连结DO,EO,
∵三棱锥A﹣BCD的各棱长都相等,E为BC中点,
∴EO∥AB,∴∠DEO是异面直线AB与DE所成角(或所成角的补角),
设三棱锥A﹣BCD的各棱长为2,
则DE=DO=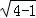 =
=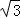 ,OE=1,
,OE=1,
∴cos∠DEO=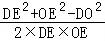 =
=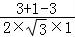 =
= .
.
∴异面直线AB与DE所成角的余弦值为 .
.
故选:B.
已知函数f(x)=(sinx+cosx)cosx,则下列说法正确的为( )
A.函数f(x)的最小正周期为2π
B.f(x)在[ ,
, ]单调递减
]单调递减
C.f(x)的图象关于直线x=﹣ 对称
对称
D.将f(x)的图象向右平移 ,再向下平移
,再向下平移 个单位长度后会得到一个奇函数的图象
个单位长度后会得到一个奇函数的图象
知识点:6.三角函数的图像与性质
D
【考点】H1:三角函数的周期性及其求法;H5:正弦函数的单调性.
【分析】化函数f(x)为正弦型函数,再判断选项中的命题是否正确.
【解答】解:函数f(x)=(sinx+cosx)cosx
=sinxcosx+cos2x
=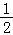 sin2x+
sin2x+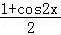
=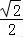 (
(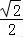 sin2x+
sin2x+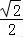 cos2x)+
cos2x)+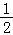
=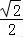 sin(2x+
sin(2x+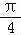 )+
)+ ,
,
∴f(x)的最小正周期为T=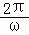 =π,∴A错误;
=π,∴A错误;
x∈[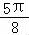 ,
,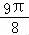 ]时,2x+
]时,2x+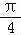 ∈[
∈[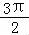 ,
,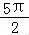 ],
],
f(x)是单调递增函数,∴B错误;
当x=﹣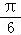 时,f(x)=
时,f(x)=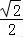 sin(﹣
sin(﹣ +
+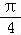 )+
)+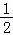 =
=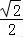 sin(﹣
sin(﹣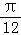 )+
)+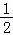 ,
,
∴x=﹣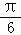 不是f(x)的对称轴,C错误;
不是f(x)的对称轴,C错误;
将f(x)的图象向右平移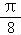 ,得y=
,得y=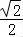 sin2[(x﹣
sin2[(x﹣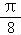 )+
)+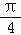 ]+
]+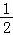 的图象,
的图象,
再向下平移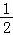 个单位长度得y=
个单位长度得y=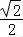 sin2x的图象,它是奇函数,D正确.
sin2x的图象,它是奇函数,D正确.
故选:D.
已知数列{an}的前n项和Sn=n2﹣n,正项等比数列{bn}中,b2=a3,bn+3bn﹣1=4 (n≥2)n∈N+,则log2bn=( )
(n≥2)n∈N+,则log2bn=( )
A.n﹣1 B.2n﹣1 C.n﹣2 D.n
知识点:4.等比数列及其性质
D
【考点】8H:数列递推式.
【分析】利用a3=S3﹣S2,即可得到log2b2.验证可知A,B,C均不符合,即可得出.
【解答】解:∵a3=S3﹣S2=(32﹣3)﹣(22﹣2)=4,∴b2=a3=4,log2b2=log24=2.
验证可知A,B,C均不符合,
故答案为D.
已知实数x,y满足 时,z=
时,z= (a≥b>0)的最大值为1,则a+b的最小值为( )
(a≥b>0)的最大值为1,则a+b的最小值为( )
A.7 B.8 C.9 D.10
知识点:3.二元一次不等式(组)与简单的线性规划
D
【考点】7C:简单线性规划.
【分析】作出不等式组对应的平面区域,利用z的最大值,确定最优解,然后利用基本不等式进行判断.
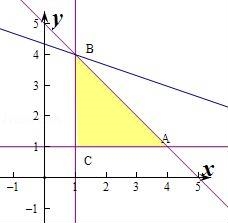
【解答】解:作出不等式组对应的平面区域如图:
由z=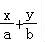 (a≥b>0)得y=
(a≥b>0)得y=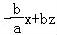 ,
,
则斜率k= ,
,
则由图象可知当直线y=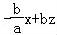 经过点B(1,4)时,
经过点B(1,4)时,
直线y=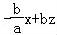 的截距最大,
的截距最大,
此时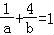 ,
,
则a+b=(a+b)(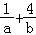 )=1+4+
)=1+4+
 ,
,
当且仅当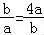 ,即b=2a取等号此时不成立,故基本不等式不成立.
,即b=2a取等号此时不成立,故基本不等式不成立.
设t=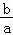 ,
,
∵a≥b>0,
∴0<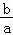 ≤1,即0<t≤1,
≤1,即0<t≤1,
则1+4+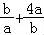 =5+t+
=5+t+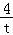 在(0,1]上单调递减,
在(0,1]上单调递减,
∴当t=1时,
1+4+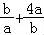 =5+t+
=5+t+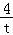 取得最小值为
取得最小值为
5+1+4=10.
即a+b的最小值为10,
故选:D.
如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( )

A.8+8 +4
+4 B.8+8
B.8+8 +2
+2 C.2+2
C.2+2 +
+ D.
D. +
+ +
+
知识点:2.空间几何体的三视图和直观图
A
【考点】L!:由三视图求面积、体积.
【分析】由三视图可知几何体为从边长为4的正方体切出来的三棱锥.作出直观图,计算各棱长求面积.
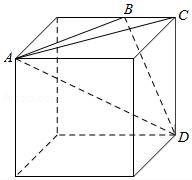
【解答】解:由三视图可知几何体为从边长为4的正方体切出来的三棱锥A﹣BCD.作出直观图如图所示:
其中A,C,D为正方体的顶点,B为正方体棱的中点.
∴S△ABC=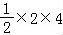 =4,S△BCD=
=4,S△BCD=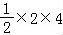 =4.
=4.
∵AC=4 ,AC⊥CD,∴S△ACD=
,AC⊥CD,∴S△ACD=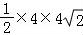 =8
=8 ,
,
由勾股定理得AB=BD=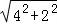 =2
=2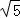 ,AD=4
,AD=4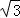 .
.
∴cos∠ABD=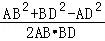 =﹣
=﹣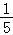 ,∴sin∠ABD=
,∴sin∠ABD=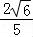 .
.
∴S△ABD=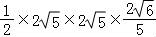 =4
=4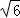 .
.
∴几何体的表面积为8+8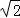 +4
+4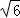 .
.
故选A.
若∀x∈R,函数f(x)=2mx2+2(4﹣m)x+1与g(x)=mx的值至少有一个为正数,则实数m的取值范围为( )
A.(0,4] B.(0,8) C.(2,5) D.(﹣∞,0)
知识点:13.函数与方程
B
【考点】52:函数零点的判定定理.
【分析】当m≤0时,显然不成立;当m>0时,g(x)=mx<0,因为f(0)=1>0,所以仅对对称轴进行讨论即可.
【解答】解:当m<0时,当x>0时,g(x)=mx<0,
又二次函数f(x)=2mx2﹣(8﹣2m)x+1开口向下,
当x→+∞时,f(x)=2mx2﹣(8﹣2m)x+1<0,故当m<0时不成立;
当m=0时,因f(0)=1>0,不符合题意;
当m>0时,
若﹣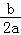 =
=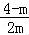 ≥0,即0<m≤4时结论显然成立;
≥0,即0<m≤4时结论显然成立;
若﹣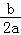 =
=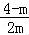 <0,时只要△=4(4﹣m)2﹣8m=4(m﹣8)(m﹣2)<0即可,即4<m<8,
<0,时只要△=4(4﹣m)2﹣8m=4(m﹣8)(m﹣2)<0即可,即4<m<8,
综上:0<m<8.
故选:B.
已知函数f(x)= ,若对任意的x∈[1,2],f′(x)•x+f(x)>0恒成立,则实数t的取值范围是( )
,若对任意的x∈[1,2],f′(x)•x+f(x)>0恒成立,则实数t的取值范围是( )
A.(﹣∞, ] B.(﹣∞,
] B.(﹣∞, ) C.(﹣∞,
) C.(﹣∞, ] D.[
] D.[ ,+∞)
,+∞)
知识点:3.导数在研究函数中的应用
B
【考点】6E:利用导数求闭区间上函数的最值;6B:利用导数研究函数的单调性.
【分析】对任意的x∈[1,2],f′(x)•x+f(x)>0恒成立⇔对任意的x∈[1,2],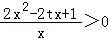 恒成立,
恒成立,
⇔对任意的x∈[1,2],2x2﹣2tx+1>0恒成立,⇔t< 恒成立,求出x+
恒成立,求出x+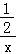 在[1,2]上的最小值即可.
在[1,2]上的最小值即可.
【解答】解:∵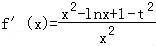
∴对任意的x∈[1,2],f′(x)•x+f(x)>0恒成立⇔对任意的x∈[1,2],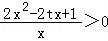 恒成立,
恒成立,
⇔对任意的x∈[1,2],2x2﹣2tx+1>0恒成立,⇔t<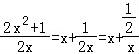 恒成立,
恒成立,
又g(x)=x+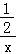 在[1,2]上单调递增,∴
在[1,2]上单调递增,∴ ,
,
∴t<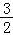 .
.
故选:B
在△ABC中,P为中线AM上的一个动点,若| |=2,则
|=2,则 •(
•( +
+ )的最小值为 .
)的最小值为 .
知识点:4.平面向量的数量积(夹角、模)
﹣2
【考点】9R:平面向量数量积的运算.
【分析】由已知中△ABC中,P为中线AM上的一个动点,若|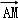 |=2,我们易将
|=2,我们易将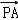 •(
•(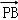 +
+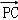 )转化为2(|
)转化为2(|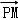 |﹣1)2﹣2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
|﹣1)2﹣2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
【解答】解:∵AM为△ABC的中线,故M为BC的中点
则 +
+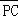 =2
=2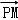
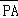 =
=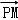 +
+
则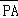 •(
•(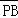 +
+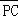 )=(
)=( +
+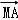 )•2
)•2
=2 2+2
2+2 •
•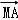
=2| |2﹣4|
|2﹣4|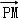 |
|
=2(|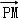 |﹣1)2﹣2
|﹣1)2﹣2
当|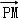 |=1时,
|=1时, •(
•(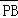 +
+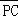 )的最小值为﹣2
)的最小值为﹣2
故答案为:﹣2
在平面直角坐标系xOy中,已知圆C:(x﹣a)2+(y﹣a+2)2=1,点A(0,﹣3),若圆C上存在点M,满足|AM|=2|MO|,则实数a的取值范围是 .
知识点:4.直线与圆的位置关系
[0,3]
【考点】J5:点与圆的位置关系;IR:两点间的距离公式.
【分析】设点M(x,y),由题意得x2+(y﹣2)2+x2+y2=10,若圆C上存在点M满足MA2+MO2=10也就等价于圆E与圆C有公共点,由此能求出实数a的取值范围.
【解答】解:设点M(x,y),由题意得点A(0,2),O(0,0)及MA2+MO2=10,
即x2+(y﹣2)2+x2+y2=10,整理得x2+(y﹣1)2=4,
即点M在圆E:x2+(y﹣1)2=4上.
若圆C上存在点M满足MA2+MO2=10也就等价于圆E与圆C有公共点,
所以|2﹣1|≤CE≤2+1,
即|2﹣1|≤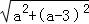 ≤2+1,
≤2+1,
整理得1≤2a2﹣6a+9≤9,解得0≤a≤3,
即实数a的取值范围是[0,3].
故答案为:[0,3].
已知等比数列{an}的首项为 ,公比为﹣
,公比为﹣ ,前n项和为Sn,则当n∈N*时,Sn﹣
,前n项和为Sn,则当n∈N*时,Sn﹣ 的最大值与最小值之和为 .
的最大值与最小值之和为 .
知识点:5.等比数列的前n项和
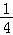
【考点】89:等比数列的前n项和.
【分析】根据等比数列的求和公式求出Sn,分n为奇数或偶数计算出Sn的范围,从而得出Sn﹣ 的最大值与最小值.
的最大值与最小值.
【解答】解:Sn=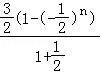 =1﹣(﹣
=1﹣(﹣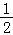 )n,
)n,
(1)当n为奇数时,Sn=1+ ,∴1<Sn≤
,∴1<Sn≤ ,
,
(2)当n为偶数时,Sn=1﹣ ,∴
,∴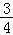 ≤Sn<1.
≤Sn<1.
∴对于任意n∈N*,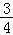 ≤Sn≤
≤Sn≤ .
.
令Sn=t,f(t)=t﹣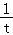 ,则f(t)在[
,则f(t)在[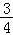 ,
, ]上单调递增,
]上单调递增,
∴f(t)的最小值为f(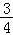 )=﹣
)=﹣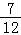 ,f(t)的最大值为f(
,f(t)的最大值为f( )=
)=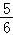 ,
,
∴Sn﹣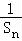 的最小值为﹣
的最小值为﹣ ,最大值为
,最大值为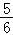 ,
,
∴Sn﹣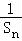 的最大值与最小值之和为﹣
的最大值与最小值之和为﹣ +
+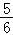 =
=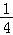 .
.
故答案为: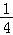 .
.
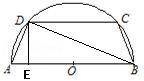
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,则梯形周长的最大值为 .

知识点:8.三角函数模型的简单应用
10
【考点】5D:函数模型的选择与应用.
【分析】作DE⊥AB于E,连接BD,根据相似关系求出AE,而CD=AB﹣2AE,从而求出梯形ABCD的周长y与腰长x间的函数解析式,根据AD>0,AE>0,CD>0,可求出定义域;利用二次函数在给定区间上求出最值的知识可求出函数的最大值.
【解答】解:如图,作DE⊥AB于E,连接BD.
因为AB为直径,所以∠ADB=90°.
在Rt△ADB与Rt△AED中,∠ADB=90°=∠AED,∠BAD=∠DAE,
所以Rt△ADB∽Rt△AED.
所以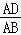 =
= ,即AE=
,即AE=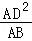 .
.
又AD=x,AB=4,所以AE=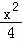 .
.
所以CD=AB﹣2AE=4﹣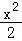 ,
,
于是y=AB+BC+CD+AD=4+x+4﹣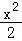 +x=﹣
+x=﹣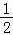 x2+2x+8
x2+2x+8
由于AD>0,AE>0,CD>0,所以x>0,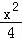 >0,4﹣
>0,4﹣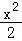 >0,
>0,
解得0<x<2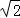 ,
,
故所求的函数为y=﹣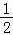 x2+2x+8(0<x<2)
x2+2x+8(0<x<2)
y=﹣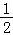 x2+2x+8=﹣
x2+2x+8=﹣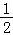 (x﹣2)2+10,
(x﹣2)2+10,
又0<x<2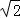 ,所以,当x=2时,y有最大值10.
,所以,当x=2时,y有最大值10.
已知函数f(x)= sin2x﹣cos2x+
sin2x﹣cos2x+ ,x∈R.
,x∈R.
(1)若∀x∈[ ,
, ],f(x)﹣m=0有两个不同的根,求m的取值范围;
],f(x)﹣m=0有两个不同的根,求m的取值范围;
(2)已知△ABC的内角A、B、C的对边分别为a、b、c,若f(B)= ,b=2,且sinA、sinB、sinC成等差数列,求△ABC的面积.
,b=2,且sinA、sinB、sinC成等差数列,求△ABC的面积.
知识点:4.和角公式与倍(半)角公式
【考点】GL:三角函数中的恒等变换应用;H2:正弦函数的图象.
【分析】(1)化简f(x),问题转化为y=m和y=f(x)在x∈[ ,
,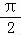 ]有2个不同的交点,画出函数的图象,求出m的范围即可;
]有2个不同的交点,画出函数的图象,求出m的范围即可;
(2)求出B的值,根据正弦定理得到a+c=2b=4,根据余弦定理得到b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣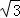 ac,求出ac的值,从而求出三角形的面积即可.
ac,求出ac的值,从而求出三角形的面积即可.
【解答】解:(1)∵函数f(x)=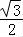 sin2x﹣cos2x+
sin2x﹣cos2x+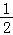 ,
,
∴f(x)=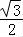 sin2x﹣
sin2x﹣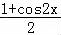 +
+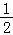 =sin(2x﹣
=sin(2x﹣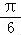 ),
),
∴f(x)=sin(2x﹣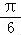 ),
),
∵x∈[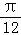 ,
, ],∴2x﹣
],∴2x﹣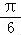 ∈[0,
∈[0,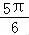 ],
],
若∀x∈[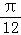 ,
,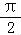 ],f(x)﹣m=0有两个不同的根,
],f(x)﹣m=0有两个不同的根,
则y=m和y=f(x)在x∈[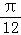 ,
,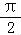 ]有2个不同的交点,
]有2个不同的交点,
画出函数的图象,如图所示:
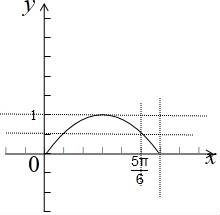 ,
,
结合图象得 ≤m<1;
≤m<1;
(2)由f(B)= ,解得:B=
,解得:B=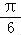 或B=
或B= ,
,
由sinA、sinB、sinC成等差数列,结合正弦定理得a+c=2b=4,
故B=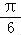 ,且b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣
,且b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣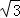 ac,
ac,
故ac=(24﹣12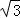 ),
),
故S△ABC=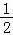 acsinB=
acsinB=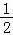 (24﹣12
(24﹣12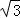 )×
)×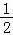 =6﹣3
=6﹣3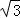 .
.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
(Ⅰ)根据直方图估计这个开学季内市场需求量x的平均数和众数;
(Ⅱ)将y表示为x的函数;
(Ⅲ)根据频率分布直方图估计利润y不少于1350元的概率.

知识点:2.用样本估计总体
【考点】B8:频率分布直方图;BB:众数、中位数、平均数.
【分析】(Ⅰ)由频率分布直方图能估计这个开学季内市场需求量x的平均数和众数.
(Ⅱ)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,当100<x≤200时,y=10x﹣5=15x﹣750,当150<x≤200时,y=10×150=1500,由此能将y表示为x的函数.
(Ⅲ)由利润不少于1350元,得150x﹣750≥750,由此能求出利润不少于1350元的概率.
【解答】解:(Ⅰ)由频率分布直方图得:最大需求量为150盒的频率为0.015×20=0.3.
这个开学季内市场需求量的众数估计值是150.
需求量为[100,120)的频率为0.005×20=0.1,
需求量为[120,140)的频率为0.01×20=0.2,
需求量为[140,160)的频率为0.015×20=0.3,
需求量为[160,180)的频率为0.0125×20=0.25,
需求量为[180,200)的频率为0.0075×20=0.15,
则平均数: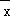 =110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153.
=110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153.
(Ⅱ)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,
所以当100<x≤200时,y=10x﹣5=15x﹣750,
当150<x≤200时,y=10×150=1500,
所以y=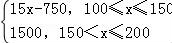 ,x∈N.
,x∈N.
(Ⅲ)因为利润不少于1350元,
所以150x﹣750≥750,解得x≥140.
所以由(Ⅰ)知利润不少于1350元的概率p=1﹣0.1﹣0.2=0.7.
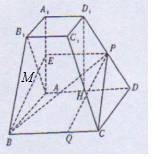
已知四棱台ABCD﹣A1B1C1D1的下底面是边长为4的正方形,AA1=4,且AA1⊥面ABCD,点P为DD1的中点,点Q在BC上,BQ=3QC,DD1与面ABCD所成角的正切值为2.
(Ⅰ)证明:PQ∥面A1ABB1;
(Ⅱ)求证:AB1⊥面PBC,并求三棱锥Q﹣PBB1的体积.

知识点:5.直线、平面平行的判定及其性质
【考点】LF:棱柱、棱锥、棱台的体积;LS:直线与平面平行的判定.
【分析】(I)取AA1中点E,连接PE、BE,过D1作D1H⊥AD于H,可证四边形PQBE为平行四边形,得出PQ∥BE,故而PQ∥面A1ABB1;
(II)由AA1⊥面ABCD可得AA1⊥BC,由相似三角形可得AB1⊥BE,故而AB1⊥平面PEBC,求出B1到平面PEBC的距离,代入体积公式即可得出棱锥的体积.
【解答】解:(Ⅰ)证明:取AA1中点E,连接PE、BE,过D1作D1H⊥AD于H.
∵AA1⊥面ABCD,AA1∥D1H,∴D1H⊥面ABCD.
∴∠D1DA为DD1与面ABCD所成角.
∴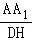 =2,又AA1=4,
=2,又AA1=4,
∴DH=2.
∴A1D1=2.
∴PE=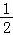 (A1D1+AD)=3,
(A1D1+AD)=3,
又EF∥AD,
∴四边形PQBE为平行四边形,
∴PQ∥BE,
又PQ⊄面A1ABB1,BE⊂面A1ABB1,
∴PQ∥面A1ABB1.
(Ⅱ)∵AA1⊥面ABCD,BC⊂平面ABCD,
∴AA1⊥BC,
又BC⊥AB,AB∩AA1=A,
∴BC⊥面ABB1A1,又AB1⊂平面ABB1A1,
∴BC⊥AB1.
在梯形A1ABB1中,Rt△BAE≌Rt△AA1B1,
∴∠B1AE+∠AEB=∠B1AE+∠AB1A1=90°,
∴AB1⊥BE,
又BE∩BC=B,BE⊂平面PEBC,BC⊂平面PEBC,
∴AB1⊥面PEBC.
设AB1∩BE=M,∵AE=2,AB=4,∴BM=2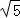 ,
,
∵A1B1=2,AA1=4,∴AB1=2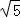 ,
,
∴AM=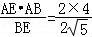 =
=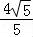 ,
,
∴B1M=AB1﹣AM=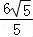 ,
,
又BQ=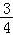 BC=3,
BC=3,
∴V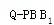 =V
=V =
= =
= =6.
=6.
已知过点P(﹣1,0)的直线l与抛物线y2=4x相交于A(x1,y1)、B(x2,y2)两点.
(Ⅰ)求直线l倾斜角的取值范围;
(Ⅱ)是否存在直线l,使A、B两点都在以M(5,0)为圆心的圆上,若存在,求出此时直线及圆的方程,若不存在,请说明理由.
知识点:3.抛物线
【考点】KN:直线与抛物线的位置关系.
【分析】(Ⅰ)设直线l的方程,代入抛物线方程,利用△>0,即可求得k的取值范围,求得直线l倾斜角的取值范围;
(Ⅱ)设圆M的方程,与抛物线方程联立,根据韦达定理,即可求得r的值及直线l的斜率k,求得直线及圆的方程.
【解答】解:(Ⅰ)由已知直线l的斜率存在且不为0.
设l:y=k(x+1),则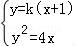 ,整理得:ky2﹣4y+4k=0,
,整理得:ky2﹣4y+4k=0,
y1+y2=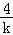 ,
,
△=16﹣4k×4k>0,解得:﹣1<k<1且k≠0.
∴直线l倾斜角的取值范围(0,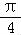 )∪(
)∪(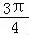 ,π);
,π);
(Ⅱ)设⊙M:(x﹣5)2+y2=r2,(r>0),
则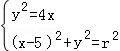 ,则x2﹣6x+25﹣r2=0,
,则x2﹣6x+25﹣r2=0,
∴x1+x2=6,
又由(Ⅰ)知y1y2=4,∴x1x2=1.
∴25﹣r2=1,∴r2=24,
并且r2=24时,方程的判别式△=36﹣4×(25﹣r2)>0,
由y1+y2=k(x1+x2+2)=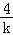 ,解得:k=±
,解得:k=±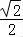 ,
,
∴存在定圆M,经过A、B两点,
其方程为:(x﹣5)2+y2=24,此时直线l方程为y=±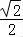 (x+1).
(x+1).
已知函数f(x)=lnx﹣ax2+(2﹣a)x.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设g(x)= ﹣2,对任意给定的x0∈(0,e],方程f(x)=g(x0)在(0,e]有两个不同的实数根,求实数a的取值范围.(其中a∈R,e=2.71828…为自然对数的底数).
﹣2,对任意给定的x0∈(0,e],方程f(x)=g(x0)在(0,e]有两个不同的实数根,求实数a的取值范围.(其中a∈R,e=2.71828…为自然对数的底数).
知识点:3.导数在研究函数中的应用
【考点】6B:利用导数研究函数的单调性;54:根的存在性及根的个数判断.
【分析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出g(x)的导数,根据函数的单调性求出a的范围即可.
【解答】解:(Ⅰ)f′(x)=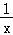 ﹣2ax+(2﹣a)=
﹣2ax+(2﹣a)=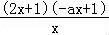 ,
,
当a=0时,f′(x)=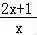 >0,f(x)在(0,+∞)单调递增.
>0,f(x)在(0,+∞)单调递增.
当a<0时,f′(x)>0,f(x)在(0,+∞)单调递增.
当a>0时,令f′(x)>0,解得:0<x<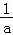 ,令f′(x)<0,解得:x>
,令f′(x)<0,解得:x>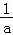 ,
,
故f(x)在(0,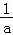 )递增,在(
)递增,在(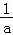 ,+∞)递减.
,+∞)递减.
(Ⅱ)g(x)=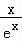 ﹣2,g′(x)=
﹣2,g′(x)= ,x∈(﹣∞,1),g′(x)>0,g(x)单调递增,
,x∈(﹣∞,1),g′(x)>0,g(x)单调递增,
x∈(1,+∞)时,g′(x)<0,g(x)单调递减,
∴x∈(0,e]时,g(x)的值域为(﹣2,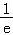 ﹣2],
﹣2],
由已知,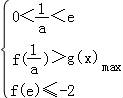 ,
,
由f(e)=1﹣ae2+2e﹣ea≤﹣2,∴a≥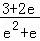 ,
,
由f(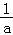 )=ln
)=ln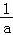 ﹣
﹣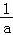 +
+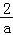 ﹣1>
﹣1>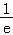 ﹣2,
﹣2,
∴lna﹣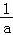 +
+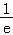 <0,
<0,
令h(x)=lnx﹣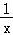 知h(x)单调递增,
知h(x)单调递增,
而h(e)=0,∴a∈(0,e)时,lna﹣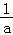 +
+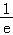 <1,
<1,
∴a∈(0,e),综合以上,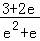 ≤a<e.
≤a<e.
在平面直角坐标系xOy中,直线l的参数方程是 (t为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为9ρ2cos2θ+16ρ2sin2θ=144,且直线l与曲线C交于P,Q两点.
(t为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为9ρ2cos2θ+16ρ2sin2θ=144,且直线l与曲线C交于P,Q两点.
(Ⅰ)求曲线C的直角坐标方程及直线l恒过的顶点A的坐标;
(Ⅱ)在(Ⅰ)的条件下,若|AP|•|AQ|=9,求直线l的普通方程.
知识点:2.坐标系与参数方程
【考点】QH:参数方程化成普通方程;Q4:简单曲线的极坐标方程.
【分析】(Ⅰ)由x=ρcosθ,y=ρsinθ,能求出曲线C的直角坐标方程,由直线l的参数方程能求出直线l恒过的定点A的坐标.
(Ⅱ)把直线l的方程代入曲线C的直角坐标方程中,得:(9+7sin2α)t2+36tcosα﹣9×12=0.由t的几何意义知|AP|=|t1|,|AQ|=|t2|,点A在椭圆内,这个方程必有两个实根,从而得到|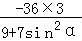 |=9,进而求出tan
|=9,进而求出tan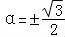 ,由此能求出直线l的方程.
,由此能求出直线l的方程.
【解答】解:(Ⅰ)∵曲线C的极坐标方程为9ρ2cos2θ+16ρ2sin2θ=144,
x=ρcosθ,y=ρsinθ,
∴曲线C的直角坐标方程为: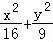 =1.
=1.
∵直线l的参数方程是 (t为参数),
(t为参数),
∴直线l恒过定点为A(2,0).
(Ⅱ)把直线l的方程代入曲线C的直角坐标方程中,
整理,得:(9+7sin2α)t2+36tcosα﹣9×12=0.
由t的几何意义知|AP|=|t1|,|AQ|=|t2|,
∵点A在椭圆内,这个方程必有两个实根,
∴t1t2= ,∵|AP|•|AQ|=|t1t2|=9,即|
,∵|AP|•|AQ|=|t1t2|=9,即| |=9,
|=9,
∴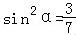 ,∵α∈(0,π),∴tan
,∵α∈(0,π),∴tan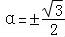 ,
,
∴直线l的方程为y=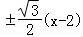 .
.
设函数f(x)=|x﹣a|,a∈R.
(Ⅰ)当a=2时,解不等式:f(x)≥6﹣|2x﹣5|;
(Ⅱ)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足2s+t=a,求证: .
.
知识点:3.不等式选讲
【考点】R5:绝对值不等式的解法.
【分析】(Ⅰ)利用绝对值的意义表示成分段函数形式,解不等式即可.
(2)根据不等式的解集求出a=3,利用1的代换结合基本不等式进行证明即可.
【解答】(Ⅰ)解:当a=2时,不等式:f(x)≥6﹣|2x﹣5|,可化为|x﹣2|+|2x﹣5|≥6.
①x≥2.5时,不等式可化为x﹣2+2x﹣5≥6,∴x≥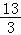 ;
;
②2≤x<2.5,不等式可化为x﹣2+5﹣2x≥6,∴x∈∅;
③x<2,不等式可化为2﹣x+5﹣2x≥6,∴x≤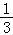 ,
,
综上所述,不等式的解集为(﹣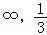 ]
]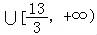 ;
;
(Ⅱ)证明:不等式f(x)≤4的解集为[a﹣4,a+4]=[﹣1,7],∴a=3,
∴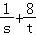 =
=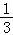 (
(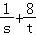 )(2s+t)=
)(2s+t)=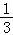 (10+
(10+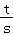 +
+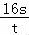 )≥6,当且仅当s=
)≥6,当且仅当s=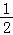 ,t=2时取等号.
,t=2时取等号.