已知角α的终边经过点P(3,
 ),则与α终边相同的角的集合是 .
),则与α终边相同的角的集合是 .
知识点:1.任意角和弧度制
{x|x=2kπ+ ,k∈Z}
,k∈Z}
【考点】G2:终边相同的角;G9:任意角的三角函数的定义.
已知sin(α+ )=
)=
 ,则cos(2α﹣
,则cos(2α﹣ )的值是
)的值是  .
.
知识点:4.和角公式与倍(半)角公式
﹣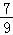
【考点】GQ:两角和与差的正弦函数;GS:二倍角的正弦.
【分析】首先,化简已知sin(α+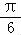 )=cos(
)=cos(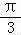 ﹣α)=
﹣α)=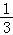
 ,然后,借助于二倍角的余弦公式求解.
,然后,借助于二倍角的余弦公式求解.
【解答】解:sin(α+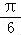 )=cos(
)=cos(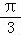 ﹣α)=
﹣α)=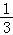

∴cos(2a﹣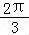 )
)
=cos(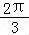 ﹣2α)
﹣2α)
=2cos2(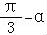 )﹣1
)﹣1
=2×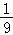
 ﹣1
﹣1
=﹣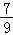
 ,
,
故答案为:﹣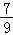
 .
.
将函数 的图象上的所有点向右平移
的图象上的所有点向右平移 个单位,再将图象上所有点的横坐标变为原来的
个单位,再将图象上所有点的横坐标变为原来的
 倍(纵坐标不变),则所得的图象的函数解析式为 .
倍(纵坐标不变),则所得的图象的函数解析式为 .
知识点:7.函数y=Asin(wx+@)+B
y=sin4x
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.
【分析】按照左加右减的原则,求出函数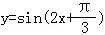 所有点向右平移
所有点向右平移 个单位的解析式,然后求出将图象上所有点的横坐标变为原来的
个单位的解析式,然后求出将图象上所有点的横坐标变为原来的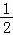
 倍时的解析式即可.
倍时的解析式即可.
【解答】解:将函数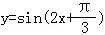 的图象上的所有点向右平移
的图象上的所有点向右平移
 个单位,得到函数
个单位,得到函数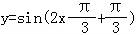 =sin2x,
=sin2x,
再将图象上所有点的横坐标变为原来的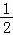
 倍(纵坐标不变),
倍(纵坐标不变),
则所得的图象的函数解析式为y=sin4x.
故答案为:y=sin4x.
若3sinα+cosα=0,则 的值为
的值为  .
.
知识点:2.任意角的三角函数
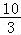
【考点】GH:同角三角函数基本关系的运用.
【分析】运用同角的商数关系,求得tanα,再将所求式子分子用平方关系,再分子分母同除以cos2α,代入计算即可得到所求值.
【解答】解:3sinα+cosα=0,
则有tanα=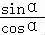 =﹣
=﹣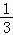
 ,
,
则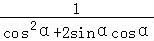 =
=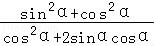
=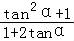 =
=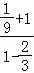 =
= .
.
故答案为: .
.
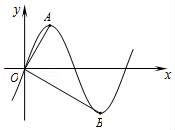
已知A,B分别是函数f(x)=2sinωx(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB= ,则该函数的最小正周期是
,则该函数的最小正周期是  .
.
知识点:7.函数y=Asin(wx+@)+B
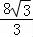
【考点】H1:三角函数的周期性及其求法.
【分析】由题意利用勾股定理可得[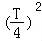 +22]+
+22]+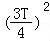 +22]=
+22]=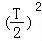 +42,由此求得T的值,可得结论.
+42,由此求得T的值,可得结论.
【解答】解:A,B分别是函数f(x)=2sinωx(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,
且∠AOB=
 ,
,
由题意可得∠AOB= ,∴由勾股定理可得[
,∴由勾股定理可得[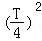 +22]+
+22]+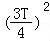 +22]=
+22]=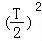 +42,
+42,
求得T=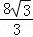 ,
,
故答案为: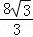 .
.
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知△ABC的面积为3 ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣
 ,则a的值为 .
,则a的值为 .
知识点:9.正弦定理和余弦定理(解三角形)
8
【考点】HR:余弦定理.
【分析】由cosA=﹣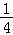
 ,A∈(0,π),可得sinA=
,A∈(0,π),可得sinA=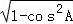 .利用S△ABC=
.利用S△ABC= =
=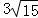 ,化为bc=24,又b﹣c=2,解得b,c.由余弦定理可得:a2=b2+c2﹣2bccosA即可得出.
,化为bc=24,又b﹣c=2,解得b,c.由余弦定理可得:a2=b2+c2﹣2bccosA即可得出.
【解答】解:∵A∈(0,π),∴sinA=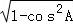 =
=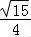 .
.
∵S△ABC= =
=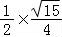 bc=
bc=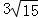 ,化为bc=24,
,化为bc=24,
又b﹣c=2,解得b=6,c=4.
由余弦定理可得:a2=b2+c2﹣2bccosA=36+16﹣48×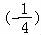
 =64.
=64.
解得a=8.
故答案为:8.
已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为  .
.
知识点:6.三角函数的图像与性质
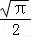
【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】由两角和的正弦函数公式化简解析式可得f(x)=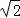 sin(ωx+
sin(ωx+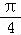 ),由2kπ﹣
),由2kπ﹣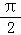
 ≤ωx+
≤ωx+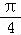
 ≤2kπ+
≤2kπ+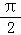 ,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:﹣ω≥
,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:﹣ω≥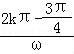 ①,ω≤
①,ω≤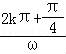 ②,k∈Z,从而解得k=0,又由ωx+
②,k∈Z,从而解得k=0,又由ωx+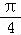
 =kπ+
=kπ+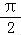
 ,可解得函数f(x)的对称轴为:x=
,可解得函数f(x)的对称轴为:x=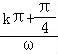 ,k∈Z,结合已知可得:ω2=
,k∈Z,结合已知可得:ω2=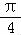
 ,从而可求ω的值.
,从而可求ω的值.
【解答】解:∵f(x)=sinωx+cosωx=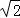
 sin(ωx+
sin(ωx+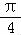 ),
),
∵函数f(x)在区间(﹣ω,ω)内单调递增,ω>0
∴2kπ﹣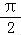 ≤ωx+
≤ωx+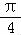 ≤2kπ+
≤2kπ+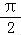 ,k∈Z可解得函数f(x)的单调递增区间为:[
,k∈Z可解得函数f(x)的单调递增区间为:[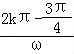 ,
,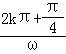 ],k∈Z,
],k∈Z,
∴可得:﹣ω≥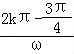 ①,ω≤
①,ω≤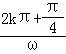 ②,k∈Z,
②,k∈Z,
∴解得:0<ω2≤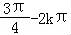 且0<ω2≤2k
且0<ω2≤2k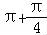 ,k∈Z,
,k∈Z,
解得:﹣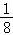

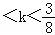 ,k∈Z,
,k∈Z,
∴可解得:k=0,
又∵由ωx+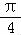 =kπ+
=kπ+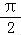 ,可解得函数f(x)的对称轴为:x=
,可解得函数f(x)的对称轴为:x=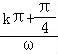 ,k∈Z,
,k∈Z,
∴由函数y=f(x)的图象关于直线x=ω对称,可得:ω2=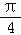 ,可解得:ω=
,可解得:ω= .
.
故答案为: .
.
若sinα>0,且tanα<0,则角α的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
知识点:2.任意角的三角函数
B
【考点】G3:象限角、轴线角.
【分析】由sinα>0,则角α的终边位于一二象限,由tanα<0,则角α的终边位于二四象限,两者结合即可解决问题.
【解答】解:∵sinα>0,则角α的终边位于一二象限,
∵由tanα<0,
∴角α的终边位于二四象限,
∴角α的终边位于第二象限.
故选择B.
下列结论中错误的是( )
A.若0<α<
 ,则sinα<tanα
,则sinα<tanα
B.若α是第二象限角,则
 为第一象限或第三象限角
为第一象限或第三象限角
C.若角α的终边过点P(3k,4k)(k≠0),则sinα=

D.若扇形的周长为6,半径为2,则其中心角的大小为1弧度
知识点:2.任意角的三角函数
C
【考点】G9:任意角的三角函数的定义.
【分析】利用任意角的三角函数的定义,象限角的定义,判断各个选项是否正确,从而得出结论.
【解答】解:若0<α< ,则sinα<tanα=
,则sinα<tanα=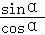 ,故A正确;
,故A正确;
若α是第二象限角,即α(2kπ,2kπ+π),k∈Z,则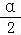 ∈(kπ,kπ+
∈(kπ,kπ+ ),为第一象限或第三象限,故B正确;
),为第一象限或第三象限,故B正确;
若角α的终边过点P(3k,4k)(k≠0),则sinα=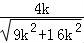 =
=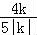 ,不一定等于
,不一定等于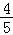
 ,故C不正确;
,故C不正确;
若扇形的周长为6,半径为2,则弧长=6﹣2×2=2,其中心角的大小为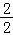
 =1弧度,
=1弧度,
故选:C.
函数y=1﹣2sin2(x﹣ )是( )
)是( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为
 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为
 的偶函数
的偶函数
知识点:4.和角公式与倍(半)角公式
A
【考点】H1:三角函数的周期性及其求法.
【分析】利用二倍角公式化简函数的解析式为y=﹣sin2x,从而得出结论.
【解答】解: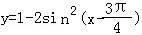 =cos(2x﹣
=cos(2x﹣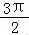 )=cos(
)=cos(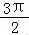 ﹣2x)=﹣sin2x,
﹣2x)=﹣sin2x,
故函数y是最小正周期为π的奇函数,
故选:A.
已知函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x=
 时,函数f(x)取得最小值,则下列结论正确的是( )
时,函数f(x)取得最小值,则下列结论正确的是( )
A.f(2)<f(﹣2)<f(0) B.f(0)<f(2)<f(﹣2)
C.f(﹣2)<f(0)<f(2) D.f(2)<f(0)<f(﹣2)
知识点:7.函数y=Asin(wx+@)+B
A
【考点】H1:三角函数的周期性及其求法.
【分析】依题意可求ω=2,又当x=
 时,函数f(x)取得最小值,可解得φ,从而可求解析式f(x)=Asin(2x+
时,函数f(x)取得最小值,可解得φ,从而可求解析式f(x)=Asin(2x+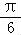 ),利用正弦函数的图象和性质及诱导公式即可比较大小.
),利用正弦函数的图象和性质及诱导公式即可比较大小.
【解答】解:依题意得,函数f(x)的周期为π,
∵ω>0,
∴ω=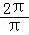 =2.
=2.
又∵当x= 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,
∴2× +φ=2kπ+
+φ=2kπ+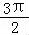 ,k∈Z,可解得:φ=2kπ+
,k∈Z,可解得:φ=2kπ+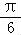
 ,k∈Z,
,k∈Z,
∴f(x)=Asin(2x+2kπ+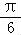 )=Asin(2x+
)=Asin(2x+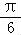 ).
).
∴f(﹣2)=Asin(﹣4+ )=Asin(
)=Asin( ﹣4+2π)>0.
﹣4+2π)>0.
f(2)=Asin(4+ )<0,
)<0,
f(0)=Asin =Asin
=Asin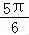 >0,
>0,
又∵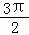 >
> ﹣4+2π>
﹣4+2π>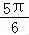 >
>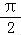 ,而f(x)=Asinx在区间(
,而f(x)=Asinx在区间(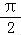 ,
,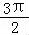 )是单调递减的,
)是单调递减的,
∴f(2)<f(﹣2)<f(0).
故选:A.
已知 tanα=2.
(1)求tan(α+ )的值;
)的值;
(2)求 的值.
的值.
知识点:5.三角函数的求值、化简与证明
【考点】GR:两角和与差的正切函数;GI:三角函数的化简求值.
【分析】(1)直接利用两角和的正切函数求值即可.
(2)利用二倍角公式化简求解即可.
【解答】解:tanα=2.
(1)tan(α+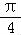 )=
)=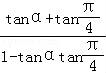 =
=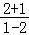 =﹣3;
=﹣3;
(2)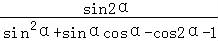 =
=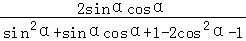 =
=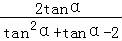 =
=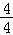
 =1.
=1.
已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.
(Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a=
 ,求△ABC的面积.
,求△ABC的面积.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】HP:正弦定理;HR:余弦定理.
【分析】(I)sin2B=2sinAsinC,由正弦定理可得:b2=2ac,再利用余弦定理即可得出.
(II)利用(I)及勾股定理可得c,再利用三角形面积计算公式即可得出.
【解答】解:(I)∵sin2B=2sinAsinC,
由正弦定理可得: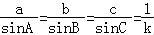 >0,
>0,
代入可得(bk)2=2ak•ck,
∴b2=2ac,
∵a=b,∴a=2c,
由余弦定理可得:cosB=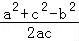 =
= =
=
 .
.
(II)由(I)可得:b2=2ac,
∵B=90°,且a=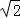 ,
,
∴a2+c2=b2=2ac,解得a=c=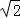 .
.
∴S△ABC=
 =1.
=1.
已知实数x满足32x﹣4﹣
 •3x﹣1+9≤0,且
•3x﹣1+9≤0,且
 .
.
(1)求实数x的取值范围;
(2)求f(x)的最大值和最小值,并求此时x的值.
知识点:10.对数函数及其性质
【考点】3H:函数的最值及其几何意义.
【分析】(1)转化为二次不等式求解即可.
(2)根据对数的运算法则,化简f(x),利用换元法,转化为二次函数求解值域.
【解答】解:(1)由32x﹣4﹣
 •3x﹣1+9≤0,
•3x﹣1+9≤0,
得32x﹣4﹣10•3x﹣2+9≤0,
即(3x﹣2﹣1)(3x﹣2﹣9)≤0,
∴1≤3x﹣2≤9,
∴2≤x≤4,
∴实数x的取值范围
(2)∵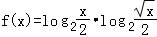 =(log2x﹣1)(
=(log2x﹣1)(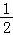
 log2x﹣1)=
log2x﹣1)=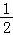
 (log2x﹣1)(log2x﹣2),
(log2x﹣1)(log2x﹣2),
设log2x=t,则t∈,
∴f(t)=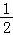 (t﹣1)(t﹣2)=
(t﹣1)(t﹣2)=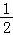 (t2﹣3t+2)=
(t2﹣3t+2)=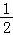 (t﹣
(t﹣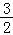 )2﹣
)2﹣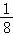 ,
,
∵f(t)在上递减,在[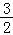 ,2]上递增,
,2]上递增,
∴f(x)min=f(t)min=f(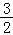 )=﹣
)=﹣ ,此时log2x=
,此时log2x=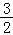 ,解得x=2
,解得x=2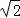
 ,
,
f(x)max=f(t)max=f(1)=f(2)=0,此时当log2x=1或log2x=2,即x=2或x=4时.
已知函数f(x)=sin2wx﹣sin2(wx﹣ )(x∈R,w为常数且
)(x∈R,w为常数且
 <w<1),函数f(x)的图象关于直线x=π对称.
<w<1),函数f(x)的图象关于直线x=π对称.
(I)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若a=1,f( A)=
A)= .求△ABC面积的最大值.
.求△ABC面积的最大值.
知识点:7.函数y=Asin(wx+@)+B
【考点】H2:正弦函数的图象;GL:三角函数中的恒等变换应用.
【分析】(1)化简f(x),根据对称轴求出ω,得出f(x)的解析式,利用周期公式计算周期;
(2)由f(
 A)=
A)=
 解出A,利用余弦定理和基本不等式得出bc的最大值,代入面积公式得出面积的最大值.
解出A,利用余弦定理和基本不等式得出bc的最大值,代入面积公式得出面积的最大值.
【解答】解:(I)f(x)=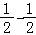 cos2ωx﹣[
cos2ωx﹣[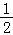 ﹣
﹣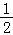 cos(2ωx﹣
cos(2ωx﹣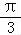 )]=
)]=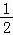 cos(2ωx﹣
cos(2ωx﹣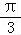 )﹣
)﹣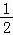
 cos2ωx=﹣
cos2ωx=﹣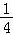 cos2ωx+
cos2ωx+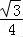 sin2ωx=
sin2ωx=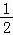
 sin(2ωx﹣
sin(2ωx﹣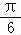 ).
).
令2ωx﹣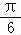 =
=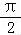 +kπ,解得x=
+kπ,解得x=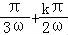 .∴f(x)的对称轴为x=
.∴f(x)的对称轴为x=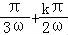 ,
,
令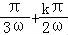 =π解得ω=
=π解得ω=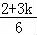 .∵
.∵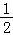
 <w<1,∴当k=1时,ω=
<w<1,∴当k=1时,ω=
 .
.
∴f(x)=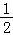
 sin(
sin(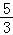
 x﹣
x﹣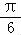 ).
).
∴f(x)的最小正周期T=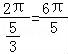 .
.
(2)∵f(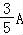 )=
)=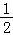
 sin(A﹣
sin(A﹣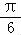 )=
)=
 ,∴sin(A﹣
,∴sin(A﹣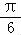 )=
)=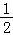
 .∴A=
.∴A=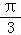
 .
.
由余弦定理得cosA=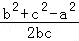 =
=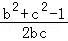 =
=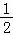
 .∴b2+c2=bc+1≥2bc,∴bc≤1.
.∴b2+c2=bc+1≥2bc,∴bc≤1.
∴S△ABC= =
=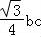 ≤
≤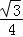 .
.
∴△ABC面积的最大值是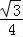
 .
.
甲、乙两人解关于x的方程:log2x+b+clogx2=0,甲写错了常数b,得两根 ,
, ;乙写错了常数c,得两根
;乙写错了常数c,得两根 ,64.求这个方程的真正根.
,64.求这个方程的真正根.
知识点:9.对数与对数运算
【考点】4H:对数的运算性质.
【分析】利用对数的换底公式可把方程化简为,(log2x)2+blog2x+c=0,令t=log2x,则 t2+bt+c=0,甲写错了常数b,c正确,可用两根之积求c;乙写错了常数c,b正确,可利用两根之和求b,从而可求方程正确的根.
【解答】解:由对数的换底公式可得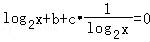
整理可得,(log2x)2+blog2x+c=0
令t=log2x,则 t2+bt+c=0
甲写错了常数b,
c=t1t2=6正确
乙写错了常数c,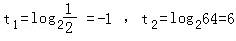
b=﹣(t1+t2)=﹣5正确
代入可得t2﹣5t+6=0,
∴t1=2t2=3
∴x1=4x2=8
已知函数 .任取t∈R,若函数f(x)在区间上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
.任取t∈R,若函数f(x)在区间上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈时,求函数g(t)的解析式;
(3)设函数h(x)=2|x﹣k|,H(x)=x|x﹣k|+2k﹣8,其中实数k为参数,且满足关于t的不等式 有解,若对任意x1∈,使得h(x2)=H(x1)成立,求实数k的取值范围.
有解,若对任意x1∈,使得h(x2)=H(x1)成立,求实数k的取值范围.
知识点:6.三角函数的图像与性质
【考点】H2:正弦函数的图象.
【分析】(1)根据正弦型函数f(x)的解析式求出它的最小正周期和对称轴方程;
(2)分类讨论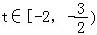 、
、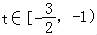 和t∈时,求出对应函数g(t)的解析式;
和t∈时,求出对应函数g(t)的解析式;
(3)根据f(x)的最小正周期T,得出g(t)是周期函数,研究函数g(t)在一个周期内的性质,求出g(t)的解析式;画出g(t)的部分图象,求出值域,利用不等式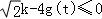 求出k的取值范围,再把“对任意x1∈,使得h(x2)=H(x1)成立”转化为“H(x)在的值域的子集“,从而求出k的取值范围.
求出k的取值范围,再把“对任意x1∈,使得h(x2)=H(x1)成立”转化为“H(x)在的值域的子集“,从而求出k的取值范围.
【解答】解:(1)函数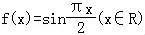 ,
,
则f(x)的最小正周期为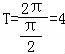 ;
;
令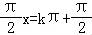 ,解得f(x)的对称轴方程为x=2k+1(x∈Z);
,解得f(x)的对称轴方程为x=2k+1(x∈Z);
(2)①当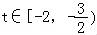 时,在区间上,
时,在区间上,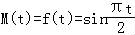 ,
,
m(t)=f(﹣1)=﹣1,
∴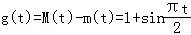 ;
;
②当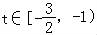 时,在区间上,
时,在区间上,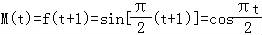 ,
,
m(t)=f(﹣1)=﹣1,
∴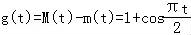 ;
;
③当t∈时,在区间上,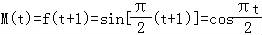 ,
,
 ,
,
∴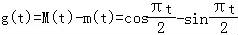 ;
;
∴当t∈时,函数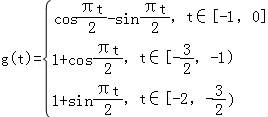 ;
;
(3)∵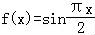 的最小正周期T=4,
的最小正周期T=4,
∴M(t+4)=M(t),m(t+4)=m(t),
∴g(t+4)=M(t+4)﹣m(t+4)=M(t)﹣m(t)=g(t);
∴g(t)是周期为4的函数,研究函数g(t)的性质,只须研究函数g(t)在t∈时的性质即可;
仿照(2),可得 ;
;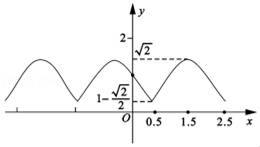
画出函数g(t)的部分图象,如图所示,
∴函数g(t)的值域为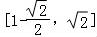 ;
;
已知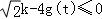 有解,即
有解,即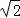 k≤4g(t)max=4
k≤4g(t)max=4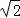 ,
,
∴k≤4;
若对任意x1∈,使得h(x2)=H(x1)成立,
即H(x)在的值域的子集.
∵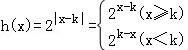 ,
,
当k≤4时,∵h(x)在(﹣∞,k)上单调递减,在上单调递增,
∴h(x)min=h(k)=1,
∵H(x)=x|x﹣k|+2k﹣8在[4,+∞)上单调递增,
∴H(x)min=H(4)=8﹣2k,
∴8﹣2k≥1,即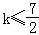 ;
;
综上,实数的取值范围是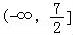 .
.