不等式3x>2的解为 .
知识点:9.对数与对数运算
x>log32
考点:指、对数不等式的解法.
专题:不等式的解法及应用.
分析:将原不等式两端同时取对数,转化为对数不等式即可.
解答: 解:∵3x>2>0,
∴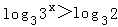 ,
,
即x>log32.
故答案为:x>log32.
点评:本题考查指数不等式的解法,将其转化为对数不等式是解题的关键,属于基础题.
设i是虚数单位,复数(a+3i)(1﹣i)是实数,则实数a= .
知识点:3.复数代数形式的四则运算
3
考点:复数代数形式的乘除运算.
专题:数系的扩充和复数.
分析:利用复数的运算法则、复数为实数的充要条件即可得出.
解答: 解:复数(a+3i)(1﹣i)=a+3+(3﹣a)i是实数,
∴3﹣a=0,解得a=3.
故答案为:3.
点评:本题考查了复数的运算法则、复数为实数的充要条件,属于基础题.
已知一个关于x,y的二元一次方程组的增广矩阵为 ,则x﹣y= .
,则x﹣y= .
知识点:4.矩阵与变换
2
考点:二阶矩阵.
专题:矩阵和变换.
分析:由增广矩阵写出原二元线性方程组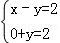 ,再根据方程求解x,y即可.
,再根据方程求解x,y即可.
解答: 解:由二元线性方程组的增广矩阵可得到
二元线性方程组的表达式 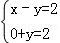 ,
,
解得 x=4,y=2,
故答案为:2.
点评:本题考查增广矩阵,解答的关键是二元线性方程组的增广矩阵的涵义,属于基础题.
已知数列{an}的前n项和Sn=n2+n,那么它的通项公式为an= .
知识点:7.数列的通项
2n
考点:等差数列的前n项和;数列递推式.
专题:等差数列与等比数列.
分析:由题意知得  ,由此可知数列{an}的通项公式an.
,由此可知数列{an}的通项公式an.
解答: 解:a1=S1=1+1=2,
an=Sn﹣Sn﹣1=(n2+n)﹣
=2n.
当n=1时,2n=2=a1,
∴an=2n.
故答案为:2n.
点评:本题主要考查了利用数列的递推公式an=Sn﹣Sn﹣1求解数列的通项公式,属于基础题.
已知 展开式中二项式系数之和为1024,则含x2项的系数为 .
展开式中二项式系数之和为1024,则含x2项的系数为 .
知识点:3.二项式定理
210
考点:二项式系数的性质.
专题:计算题;二项式定理.
分析:依题意得,由二项式系数和2n=1024,求得n的值,再求展开式的第k+1项的通项公式,再令通项公式中x的幂指数等于2,求得r的值,即可求得展开式中含x2项的系数.
解答: 解:依题意得,由二项式系数和 2n=1024,解得n=10;
由于展开式的第k+1项为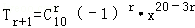 ,
,
令20﹣3r=2,解得r=6,
∴展开式中含x2项的系数为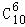 =210.
=210.
故答案为:210.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.
已知直线3x+4y+2=0与(x﹣1)2+y2=r2圆相切,则该圆的半径大小为 .
知识点:4.直线与圆的位置关系
1
考点:圆的切线方程.
专题:直线与圆.
分析:由圆的方程求出圆心坐标,直接用圆心到直线的距离等于半径求得答案.
解答: 解:由(x﹣1)2+y2=r2,可知圆心坐标为(1,0),半径为r,
∵直线3x+4y+2=0与(x﹣1)2+y2=r2圆相切,
由圆心到直线的距离d=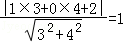 ,
,
可得圆的半径为1.
故答案为:1.
点评:本题考查了直线和圆的位置关系,考查了点到直线的距离公式的应用,是基础题.
已知x,y满足 ,则x+y的最大值为 .
,则x+y的最大值为 .
知识点:3.二元一次不等式(组)与简单的线性规划
2
考点:简单线性规划.
专题:不等式的解法及应用.
分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求x+y的最大值.
解答: 解:作出不等式组对应的平面区域如图:(阴影部分).
设z=x+y得y=﹣x+z,
平移直线y=﹣x+z,
由图象可知当直线y=﹣x+z经过点B时,直线y=﹣x+z的截距最大,
此时z最大.
由 ,解得
,解得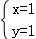 ,即B(1,1),
,即B(1,1),
代入目标函数z=x+y得z=1+1=2.
即目标函数z=x+y的最大值为2.
故答案为:2.
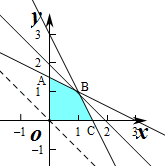
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.利用平移确定目标函数取得最优解的条件是解决本题的关键.
若对任意x∈R,不等式sin2x﹣2sin2x﹣m<0恒成立,则m的取值范围是 .
知识点:6.三角函数的图像与性质
( ﹣1,+∞)
﹣1,+∞)
考点:三角函数的最值.
专题:三角函数的求值.
分析:问题转化为m>sin2x﹣2sin2x对任意x∈R恒成立,只需由三角函数求出求t=sin2x﹣2sin2x的最大值即可.
解答: 解:∵对任意x∈R,不等式sin2x﹣2sin2x﹣m<0恒成立,
∴m>sin2x﹣2sin2x对任意x∈R恒成立,
∴只需求t=sin2x﹣2sin2x的最大值,
∵t=sin2x﹣2sin2x=sin2x﹣(1﹣cos2x)
=sin2x+cos2x﹣1= sin(2x+
sin(2x+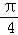 )﹣1,
)﹣1,
∴当sin(2x+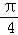 )=1时,t取最大值
)=1时,t取最大值 ﹣1,
﹣1,
∴m的取值范围为( ﹣1,+∞)
﹣1,+∞)
故答案为:(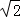 ﹣1,+∞)
﹣1,+∞)
点评:本题考查三角函数的最值,涉及恒成立问题和三角函数公式的应用,属基础题.
已知球的表面积为64πcm2,用一个平面截球,使截面球的半径为2cm,则截面与球心的距离是 cm.
知识点:11.球
2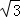
考点:球的体积和表面积.
专题:计算题;空间位置关系与距离.
分析:先求出球的半径,再利用勾股定理,即可求出截面与球心的距离.
解答: 解:球的表面积为64πcm2,则球的半径为4cm,
∵用一个平面截球,使截面球的半径为2cm,
∴截面与球心的距离是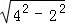 =2
=2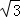 cm.
cm.
故答案为:2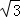 .
.
点评:本题考查截面与球心的距离,考查球的表面积,求出球的半径是关键.
已知a,b∈{1,2,3,4,5,6},直线l1:x﹣2y﹣1=0,l2:ax+by﹣1=0,则直线l1⊥l2的概率为 .
知识点:2.古典概型
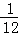
考点:直线的一般式方程与直线的垂直关系;等可能事件的概率.
专题:计算题.
分析:本题是一个等可能事件的概率,试验发生包含的事件数是36,满足条件的事件是直线l1⊥l2,得到关于a,b的关系式,写出满足条件的事件数,即可得到结果.
解答: 解:设事件A为“直线l1⊥l2”,
∵a,b∈{1,2,3,4,5,6}的总事件数为(1,1),(1,2)…,(1,6),
(2,1),(2,2),…,(2,6),…,(5,6),…,(6,6)共36种,
而l1:x﹣2y﹣1=0,l2:ax+by﹣1=0,l1⊥l2⇔1•a﹣2b=0,
∴a=2时,b=1;
a=4时,b=2;
a=6时,b=3;
共3种情形.
∴P(A)=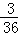 =
=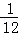 .
.
∴直线l1⊥l2的概率为: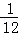 .
.
故答案为: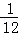
点评:本题考查等可能事件的概率,考查两条直线的垂直,关键在于掌握等可能事件的概率公式,属于中档题.
若函数 ﹣4的零点m∈(a,a+1),a为整数,则所以满足条件a的值为 .
﹣4的零点m∈(a,a+1),a为整数,则所以满足条件a的值为 .
知识点:13.函数与方程
a=1或a=﹣2
考点:函数零点的判定定理.
专题:计算题;函数的性质及应用.
分析:首先可判断函数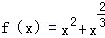 ﹣4是偶函数,且在
﹣4是偶函数,且在
【题文】
已知函数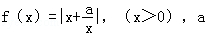 为实数.
为实数.
(1)当a=﹣1时,判断函数y=f(x)在(1,+∞)上的单调性,并加以证明;
(2)根据实数a的不同取值,讨论函数y=f(x)的最小值.
【答案】
【解析】
考点:函数的最值及其几何意义;分段函数的应用.
专题:计算题;函数的性质及应用.
分析:(1)f(x)=|x﹣ |=x﹣
|=x﹣ 在(1,+∞)上单调递增,利用f′(x)=1+
在(1,+∞)上单调递增,利用f′(x)=1+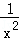 >0可得;
>0可得;
(2)a≤0时,x=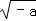 时,函数取得最小值0;a>0时,f(x)=x+
时,函数取得最小值0;a>0时,f(x)=x+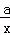 时,利用基本不等式求出y=f(x)的最小值为2
时,利用基本不等式求出y=f(x)的最小值为2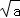 .
.
解答: 解:(1)f(x)=|x﹣ |=x﹣
|=x﹣ 在(1,+∞)上单调递增.
在(1,+∞)上单调递增.
∵f′(x)=1+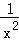 >0,
>0,
∴y=f(x)在(1,+∞)上在(1,+∞)上单调递增;
(2)a<0时,x=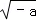 时,函数取得最小值0;a=0时函数无最小值;
时,函数取得最小值0;a=0时函数无最小值;
a>0时,f(x)=x+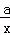 ≥2
≥2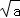 ,当且仅当x=
,当且仅当x=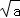 时,y=f(x)的最小值为2
时,y=f(x)的最小值为2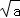 .
.
点评:本题考查函数的最值,考查导数知识的运用,考查基本不等式,属于中档题.
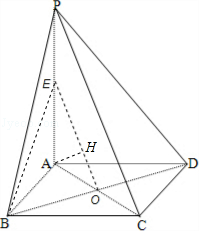
如图,在四棱锥P﹣ABCD中,底面ABCD为边长为2的正方形,PA⊥底面ABCD,PA=2
(1)求异面直线PC与BD所成角的大小;
(2)求点A到平面PBD的距离.

知识点:10.空间角与距离
考点:点、线、面间的距离计算;异面直线及其所成的角.
专题:综合题;空间位置关系与距离;空间角.
分析:(1)令AC与BD交点为O,PA的中点为E,连接OE,BE,则OE∥PC,则直线PC与BD所成角等于直线OE与BD所成角,解三角形OEB,即可得到答案.
(2)过A作AH⊥OE,垂足为H,则AH⊥平面PBD,求出AH,即可求点A到平面PBD的距离.
解答: 解:(1)令AC与BD交点为O,PA的中点为E,连接OE,BE如图所示:
∵O为BD的中点,则EO= PC=
PC=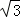 ,且OE∥PC,
,且OE∥PC,
又∵PA⊥面ABCD,且PA=AD=2,AB=2,BD=2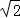 .
.
∴OB= BD=
BD=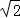 ,BE=
,BE=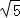 ,
,
∴|cos∠EOB|=|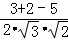 |=0,
|=0,
即异面直线PC与BD所成角为90°;
(2)过A作AH⊥OE,垂足为H,则AH⊥平面PBD.
在直角三角形AOE中,AE=1,OA=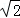 ,OE=
,OE=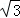 ,
,
由等面积可得AH= =
=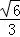 .
.
点评:本题考查异面直线及其所成的角,点A到平面PBD的距离,将空间问题转化为一个平面解三角形的问题是解题的关键.
一颗人造卫星在地球上空1630千米处沿着圆形轨道匀速运行,每2小时绕地球一周,将地球近似为一个球体,半径为6370千米,卫星轨道所在圆的圆心与地球球心重合,已知卫星与中午12点整通过卫星跟踪站A点的正上空A′,12:03时卫星通过C
点,(卫星接收天线发出的无线电信号所需时间忽略不计)
(1)求人造卫星在12:03时与卫星跟踪站A之间的距离.(精确到1千米)
(2)求此时天线方向AC与水平线的夹角(精确到1分).

知识点:10.空间角与距离
考点:球面距离及相关计算.
专题:计算题;空间位置关系与距离.
分析:(1)求出∠AOC,在△ACO中利用余弦定理,即可求人造卫星在12:03时与卫星跟踪站A之间的距离;
(2)设此时天线方向AC与水平线的夹角为φ,则∠CAO=φ+90°,所以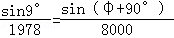 ,即可求此时天线方向AC与水平线的夹角.
,即可求此时天线方向AC与水平线的夹角.
解答: 解:(1)设∠AOC=θ,则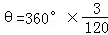 =9°.
=9°.
在△ACO中,AC2=63702+80002﹣2×6370×8000×cos9°=3911704.327,
所以AC≈1978(千米),
所以人造卫星在12:03时与卫星跟踪站A之间的距离为1978千米;
(2)设此时天线方向AC与水平线的夹角为φ,则∠CAO=φ+90°,
所以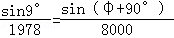 ,
,
所以sin(φ+90°)≈0.6327,
所以cosφ≈0.6327,
所以φ≈50°45′,
所以此时天线方向AC与水平线的夹角为50°45′.
点评:本题考查利用数学知识解决实际问题,考查余弦定理的运用,考查学生的计算能力,属于中档题.
(16分)已知直线l与圆锥曲线C相交于两点A,B,与x轴,y轴分别交于D、E两点,且满足

(1)已知直线l的方程为y=2x﹣4,抛物线C的方程为y2=4x,求λ1+λ2的值;
(2)已知直线l:x=my+1(m>1),椭圆C: =1,求
=1,求 的取值范围;
的取值范围;
(3)已知双曲线C: ,求点D的坐标.
,求点D的坐标.
知识点:1.椭圆
考点:直线与圆锥曲线的综合问题;抛物线的简单性质.
专题:圆锥曲线的定义、性质与方程.
分析:(1)通过直线l的方程可得D、E坐标,将y=2x﹣4代入y2=4x可得点A、B坐标,利用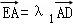 、
、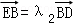 ,计算即可;
,计算即可;
(2)通过联立x=my+1(m>1)与 =1,利用韦达定理、
=1,利用韦达定理、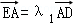 、
、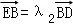 ,计算即得结论;
,计算即得结论;
(3)通过设直线l的方程并与双曲线C方程联立,利用韦达定理、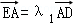 ,
,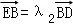 ,计算即可.
,计算即可.
解答: 解:(1)将y=2x﹣4代入y2=4x,求得点A(1,﹣2),B(4,4),
又∵D(2,0),E(0,﹣4),且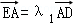 ,
,
∴(1,2)=λ1(1,2)=(λ1,2λ1),即λ1=1,
同理由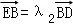 ,可得λ2=﹣2,
,可得λ2=﹣2,
∴λ1+λ2=﹣1;
(2)联立x=my+1(m>1)与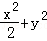 =1,
=1,
消去x可得:(2+m2)y2+2my﹣1=0,
由韦达定理可得:y1+y2=﹣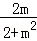 ,y1y2=﹣
,y1y2=﹣ ,
,
∵D(1,0),E(0,﹣ ),且
),且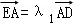 ,
,
∴y1+ =﹣λ1y1,∴λ1=﹣(1+
=﹣λ1y1,∴λ1=﹣(1+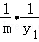 ),
),
同理由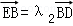 ,可得y2+
,可得y2+ =﹣λ2y2,∴λ2=﹣(1+
=﹣λ2y2,∴λ2=﹣(1+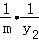 ),
),
∴λ1+λ2=﹣(1+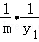 )﹣(1+
)﹣(1+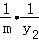 )=﹣2﹣
)=﹣2﹣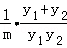 =﹣2﹣
=﹣2﹣ =﹣4,
=﹣4,
∴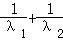 =﹣
=﹣ =
=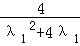 =
= ,
,
∵m>1,∴点A在椭圆上位于第三象限的部分上运动,
由分点的性质可得λ1∈(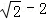 ,0),
,0),
∴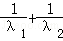 ∈(﹣∞,﹣2);
∈(﹣∞,﹣2);
(3)设直线l的方程为:x=my+t,代入双曲线C方程,
消去x得:(﹣3+m2)y2+2mty+(t2﹣3)=0,
由韦达定理可得:y1+y2=﹣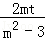 ,y1y2=﹣
,y1y2=﹣ ,∴
,∴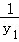 +
+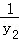 =﹣
=﹣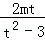 ,
,
由 ,
,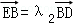 可得:﹣(λ1+λ2)=2+
可得:﹣(λ1+λ2)=2+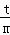 •(
•(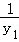 +
+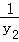 ),
),
∵λ1+λ2=6,∴2+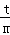 •(﹣
•(﹣ )=﹣6,解得t=±2,
)=﹣6,解得t=±2,
∴点D(±2,0);
当直线l与x轴重合时,λ1=﹣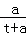 ,λ2=
,λ2=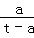 或者λ1=
或者λ1=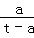 ,λ2=﹣
,λ2=﹣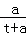 ,
,
∴都有λ1+λ2=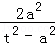 =6也满足要求,
=6也满足要求,
∴在x轴上存在定点D(±2,0).
点评:本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.
(18分)记无穷数列{an}的前n项a1,a2,…,an的最大项为An,第n项之后的各项an+1,an+2,…的最小项为Bn,令bn=An﹣Bn.
(1)若数列{an}的通项公式为an=2n2﹣n+1,写出b1,b2,并求数列{bn}的通项公式;
(2)若数列{an}递增,且{an+1﹣an}是等差数列,求证:{bn}为等差数列;
(3)若数列{bn}的通项公式为bn=1﹣2n,判断{an+1﹣an}是否为等差数列,若是,求出公差;若不是,说明理由.
知识点:2.等差数列及其性质
考点:数列递推式;等差关系的确定;等比关系的确定.
专题:等差数列与等比数列.
分析:(1)数列{an}的通项公式为an=2n2﹣n+1,可得:a1=2,an,n≥1时为单调递增数列.可得A1=a1=2,B1=a2=7,b1=﹣5.同理可得b2=A2﹣B2=a2﹣a3.可得数列{bn}的通项公式bn=An﹣Bn=an﹣an+1.
(2)由数列{an}递增,可得An=an,Bn=an+1,可得bn=An﹣Bn=an﹣an+1=﹣(an+1﹣an),即可证明.
(3)设d是非负整数,先证明:bn=﹣d(n=1,2,3…)的充分必要条件为{an}是公差为d的等差数列,即可得出.
解答: (1)解:数列{an}的通项公式为an=2n2﹣n+1,
a1=2,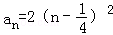 +
+ ,n≥1时为单调递增数列.
,n≥1时为单调递增数列.
∴A1=2,B1=a2=2×22﹣2+1=7
b1=2﹣7=﹣5.
同理可得b2=A2﹣B2=a2﹣a3=﹣9.
∴数列{bn}的通项公式bn=An﹣Bn=an﹣an+1=2n2﹣n+1﹣=﹣4n﹣1;
(2)证明:∵数列{an}递增,∴An=an,Bn=an+1,
∴bn=An﹣Bn=an﹣an+1=﹣(an+1﹣an),
∵{an+1﹣an}是等差数列,
∴{bn}为等差数列.
(3)解:设d是非负整数,先证明:bn=﹣d(n=1,2,3…)的充分必要条件为{an}是公差为d的等差数列;
充分性:设d是非负整数,若{an}是公差为d的等差数列,则an=a1+(n﹣1)d,
∴An=an=a1+(n﹣1)d,Bn=an+1=a1+nd,
∴dn=An﹣Bn=﹣d,(n=1,2,3,4…).
必要性:若bn=An﹣Bn=﹣d,(n=1,2,3,4…).假设ak是第一个使ak﹣ak﹣1<0的项,
则dk=Ak﹣Bk=ak﹣1﹣Bk≥ak﹣1﹣ak>0,这与dn=﹣d≤0相矛盾,
故{an}是一个不减的数列.
∴dn=An﹣Bn=an﹣an+1=﹣d,即 an+1﹣an=d,
故{an}是公差为d的等差数列.
而数列{bn}的通项公式为bn=1﹣2n,
bn+1﹣bn=﹣2,
∴{an+1﹣an}是公差为2等差数列.
点评:本题考查了新定义、等差数列的通项公式、数列的单调性、充要条件,考查了变形能力,考查了推理能力与计算能力,属于难题.