已知a、b、c、p为空间的任意向量，O、A、B、C为空间的任意点，有下列命题
①a∥b的充要条件是存在实数λ，使a＝λb
②向量p与向量a、b共面的充要条件是存在唯一的有序实数对（x，y），使p＝xa＋yb
③若向量{a、b、c}是空间的一个基底，则{a＋b，a－b，c}也可构成空间的另一个基底
④若OA、OB、OC不构成空间的一个基底，则O、A、B、C一定共面
其中真命题的个数是（ ）
A．1个 B．2个 C．3个 D．4个
知识点：5.充分条件与必要条件
B
略
如图，在正方体ABCD—A1B1C1D1中，点E1、F1分别是A1B1、C1D1的一个四等分点，则BE1与DF1所成角的余弦值为（ ）
A．0
B．
C．
D．
知识点：10.空间角与距离
D
略
在5张奖券中有3张能中奖，甲、乙两人不放回地依次抽取一张，则在甲抽到中奖奖券的条件下，乙抽到中奖奖券的概率为（ ）
A．
B．
C．
D．
知识点：1.随机事件的概率
C
略
某地区数学考试的成绩X服从正态分布，其密度曲线如图所示，成绩X位于区间（52，68]的概率是（ ）
A．0.6826 B．0.9544 C．0.9974 D．0.3413
若X~N（μ，σ2），则 P(μ－σ＜X≤μ＋σ)＝0.6826
P(μ－2σ＜X≤μ＋2σ)＝0.9544
P(μ－3σ＜X≤μ＋3σ)＝0.9974
正态分布N（μ，σ2）的密度函数为f(x)＝
e
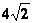
知识点：10.正态分布
A
略
设集合I＝{1，2，3，4，5}，选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同选择方法共有（ ）种
A．50 B．49 C．48 D．47
知识点：2.排列与组合
B
略
已知ABCD—A1B1C1D1是一个棱长为1的正方体，O1是底面A1B1C1D1的中心，M是棱BB1上的点，且|BM| ：|MB1|＝1 ：3，则四面体O1—ADM的体积为（ ）
A．
B．
C．
D．
知识点：3.空间几何体的表面积与体积
C
略
已知F1、F2分别为双曲线
（a＞0，b＞0）的左、右焦点，P为双曲线右支上一点，且满足|PF2|＝|F1F2|，若直线PF1与圆x2＋y2＝a2相切，则双曲线的离心率e的值为（ ）
A．2 B．
C．
D．
知识点：2.双曲线
B
略
已知直线l：y＝－
＋m与曲线C：y＝
仅有三个交点，则m的取值范围是（ ）
A．（
－2，）
B．（0，－1） C．（0，）
D．（1，）
知识点：4.直线与圆锥曲线的位置关系
D
略
过抛物线y2＝2px (p＞0)焦点F的直线与抛物线交于A、B两点，M、N为准线l上两点，AM⊥l，BN⊥l，M、N为垂足，C为线段AB中点，D为线段MN中点，CD交抛物线于点E，下列结论中正确的是 .（把你认为正确的序号都填上）
①
＋
为定值
②以AB为直径的圆与l相切
③以MN为直径的圆与AB所在直线相切
④以AF为直径的圆与y轴相切
⑤E为线段CD中点
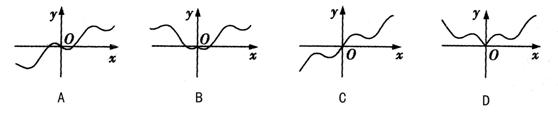
知识点：3.抛物线
①②③④⑤
略
男婴为24人，女婴为8人；出生时间在白天的男婴为31人，女婴为26人.
（1）将下面的2×2列联表补充完整；
（2）能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系？
出生时间
性别
晚上
白天
合计
男婴
女婴
合计
P(K2≥k0)
0.15
0.10
0.05
k0
2.072
2.706
3.841
K2＝
知识点：5.独立性检验的基本思想及其初步运用
解（1）
|
出生时间 性别 |
晚上 |
白天 |
合计 |
|
男婴 |
24 |
31 |
55 |
|
女婴 |
8 |
26 |
34 |
|
合计 |
32 |
57 |
89 |
（6分）
（2）由所给数据计算出K2的观测值k≈3.689，而根据表知
P（K2≥2.706）≈0.10，
而3.689＞2.706，因此在犯错误概率不超过0.1的前提下认为“婴儿的性别与出生的时间有关系”.
（12分）
略
如图，过抛物线y2＝2px (p＞0)焦点F的直线交抛物线于A、B两点，O为坐标原点，l为抛物线的准线，点D在l上。
（1）求证：“如果A、O、D三点共线，则直线DB与
x轴平行”；
（2）写出（1）中命题的逆命题，判断它是真命题还是
假命题，并说明理由.
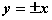
知识点：3.抛物线
（1）证明：设点A的坐标为（
，y0），则直线OA的方程为
（y0≠0） ① 抛物线的准线方程是x＝－
②
联立①②，可得点D的纵坐标为y＝－
③
（3分）
因为点F的坐标是（，0），所以直线AF的方程为y＝
(x－)
④
其中y
≠p2.联立y2＝2px与④，可得点B的纵坐标为y＝－
⑤
由③⑤可知，DB∥x轴.
当y＝p2时，结论显然成立.所以，直线DB平行于抛物线的对称轴.
（6分）
（2）逆命题：如果DB与x轴平行，则A、O、D三点共线它是真命题，证明如下
（8分）
因为抛物线y2＝2px（p＞0）的焦点为F（，0），所以经过点F的直线AB的方程可设为x＝my＋.代入抛物线方程，得y2－2pmy－p2＝0.
若记A（x1，y1），B（x2，y2），则y1，y2是该方程的两个根，所以y1y2＝－p2.
（10分）
因为DB∥x轴，且点D在准线x＝－上，所以点D的坐标为（－，y2），故直线DO的斜率为k＝
，
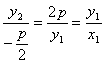即k也是直线OA的斜率，所以直线AD经过原点O，即A、O、D三点共线.
（12分）
略
如图，长方体ABCD—A1B1C1D1中，点E、F分别在BB1、DD1上，且AE⊥A1B，AF⊥A1D.
（1）求证：A1C⊥平面AEF；
（2）当AB＝4，AD＝3，AA1＝5时，
求平面AEF与平面D1B1BD所成的角的余弦值.
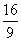
知识点：10.空间角与距离
（1）证明：因为A1C·AE＝(A1B＋BC)·AE＝BC·AE＝BC·(AB＋BE)＝0，
所以A1C⊥AE；
（3分）
因为A1C·AF＝(A1D＋DC)·AF＝DC·AF＝DC·(AD＋DF)＝0，
所以A1C⊥AF，
因此，A1C⊥平面AEF.
（6分）
→
（2）解：以点A1为原点建立坐标系，得下列坐标：A1（0，0，0），B1（4，0，0），C1（4，3，0），D1（0，3，0），A（0，0，－5），B（4，0，－5），C（4，3，－5），D（0，3，－5）.
设平面D1B1BD的法向量为a＝（x，y，0），则a·B1D1＝0，得4x＝3y.
令x＝3，y＝4，则a＝（3，4，0）. cosθ＝
＝
（12分）
略
甲乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为
，乙在每局中获胜的概率为
，且各局胜负相互独立，比赛停止时一共已打ξ局.
（1）列出随机变量ξ的分布列；（2）求ξ的期望值Eξ.
知识点：9.离散型随机变量的分布列、均值与方差
（1）证明：因为A1C·AE＝(A1B＋BC)·AE＝BC·AE＝BC·(AB＋BE)＝0，
所以A1C⊥AE；
（3分）
因为A1C·AF＝(A1D＋DC)·AF＝DC·AF＝DC·(AD＋DF)＝0，
所以A1C⊥AF，
因此，A1C⊥平面AEF.
（6分）
→
（2）解：以点A1为原点建立坐标系，得下列坐标：A1（0，0，0），B1（4，0，0），C1（4，3，0），D1（0，3，0），A（0，0，－5），B（4，0，－5），C（4，3，－5），D（0，3，－5）.
设平面D1B1BD的法向量为a＝（x，y，0），则a·B1D1＝0，得4x＝3y.
令x＝3，y＝4，则a＝（3，4，0）. cosθ＝＝
（12分）
略
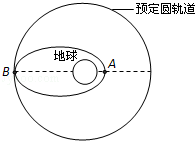
如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E、F、G分别是线段PA、PD、CD的中点.
（1）求证：PB∥平面EFG；
（2）求异面直线EG与BD所成角的余弦值；
（3）在线段CD上是否存在一点Q，使得A点到平面EFQ的距离为
，
若存在，求出CQ的值？若不存在，请说明理由.
知识点：5.直线、平面平行的判定及其性质
解法一：
（1）取AB的中点H，连接GH，HE，
∵E、F、G分别是线段PA、PD、CD的中点，
∴GH∥AD∥EF，∴E、F、H、G四点共面.
又H为AB的中点，∴EH∥PB.
又EH
面EFG，PB
平面EFG，∴PB∥平面EFG.
（4分）
（2）取BC的中点M，连接GM、AM、EM，则GM∥BD，
∴∠EGM（或其补角）就是异面直线EG与BD所成的角.
在Rt△MAE中，EM＝
＝
，
同理EG＝，又GM＝
MD＝
∴在△MGE中，cos∠EGM＝
＝
＝
，
故异面直线EG与BD所成角的余弦值为.
（8分）
（3）假设在线段CD上存在一点Q满足题设条件，过点Q作QR⊥AB于R，连接RE，则QR∥AD.
∵四边形ABCD是正方形，△PAD是直角三角形，且PA＝AD＝2，
∴AD⊥AB，AD⊥PA.又AB∩PA＝A，∴AD⊥平面PAB.
又∵E、F分别是PA、PD的中点，∴EF∥AD，∴EF⊥平面PAB.
又EF面EFQ，∴面EFQ⊥面PAB.
过A作AT⊥ER于T，则AT⊥平面EFQ，
∴AT就是点A到平面EFQ的距离.
设CQ＝x(0≤x≤2)，则BR＝CQ＝x，AR＝2－x，AE＝1，
在Rt△EAR中，AT＝
＝
＝
解得x＝
.故存在点Q，当CQ＝时，点A到平面EFQ的距离为
（13分）
解法二：建立如图所示的空间直角坐标系A—xyz，则A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），P（0，0，2），E（0，0，1），F（0，1，1），G（1，2，0）.
（1）∵PB＝（2，0，－2），FE＝（0，－1，0），FG＝（1，1，－1），
设PB＝sFE＋tFG，即(2，0，－2)＝s(0，－1，0)＋t(1，1，－1)，
 |
∴
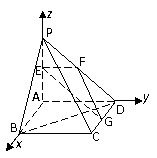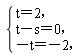解得s＝t＝2.
∴PB＝2FE＋2FG
又∵FE与FG不共线，∴PB，FE与FG共面.
∵PB平面EFG，∴PB∥平面EFG.
（4分）
（2）∵EG＝（1，2，－1），BD＝（－2，2，0）.
∴cos＜EG，BD＞＝
＝
＝
故异面直线EG与BD所成的角的余弦值为
（8分）
（3）假设线段CD上存在一点Q满足题设条件，令CQ＝m(0≤m≤2)，则DQ＝2－m，
∴点Q的坐标为（2－m，2，0）
∴EQ＝（2―m，2，―1）
而EF＝（0，1，0），设平面EFQ的法向量为n＝(x，y，z)，则
∴
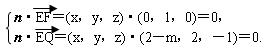
令x＝1，则n＝（1，0，2－m），又AE＝（0，0，1），
∴点A到平面EFQ的距离d＝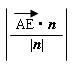
＝
＝
即(2－m)2＝
，
∴m＝或m＝
，又m＝＞2不合题意，舍去.
故存在点Q，当CQ＝时，点A到平面EFQ的距离为.
（13分）
略
已知定点A（1，0）和定直线x＝－1的两个动点E、F，满足AE⊥AF，动点P满足EP∥OA，FO∥OP（其中O为坐标原点）.
（1）求动点P的轨迹C的方程；
（2）过点B（0，2）的直线l与（1）中轨迹C相交于两个不同的点M、N，若∠MAN为钝角，求直线l的斜率的取值范围；
（3）过点T（－1，0）作直线m与（1）中的轨迹C交于两点G、H，问在x轴上是否存在一点D，使△DGH为等边三角形；若存在，试求出点D的坐标；若不存在，请说明理由.
知识点：3.抛物线
解：
（1）设P（x，y），E（－1，y1），F（－1，y2）（y1、y2均不为0），
由EP∥OA得y1＝y，即E（－1，y）.
由FO∥OP得y2＝－
，即F（―1，―），得
AE·AF＝0 
（2，－y1）·（2，y2）＝0
y1y2＝－4
y2＝4x（x≠0）
所以动点P的轨迹C的方程为y2＝4x（x≠0）.
（3分）
（2）设直线l的方程y＝kx＋2（k≠0），M（
，y1），N（
，y2）联立得
消去x得ky2－4y＋8＝0，所以y1＋y2＝
，y1y2＝
，且△＝16－32k＞0，即k＜.
所以AM·AN＝
·
＝
＋y1y2
＝
＝
＋
因为∠MAN为钝角，所以AM·AN＜0，所以－12＜k＜0.
（8分）
（3）
设m：y＝k(x＋1)（k≠0），代入y2＝4x，得k2x2＋2(k2－2)x＋k2＝0，
由，△＝[2(k2―2)]2―4k2·k2＝－16k2＋16＞0，得|k|＜1.
设G（x1，y1），H（x2，y2），则x1＋x2＝
，x1x2＝1，
所以|GH|＝
·
＝·
＝
.
GH的中点Q的坐标为（
，
）.
假设存在点D（x0，0），使△DGH为等边三角形，又边GH的中垂线方程为
y－＝―
(x―).
由D在此中垂线上，得0－＝―(x0―)，x0＝
＋1.
（11分）
设d为D到直线l的距离，由正三角形的条件有
|GH|＝d，可得
，
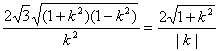即3(1－k2)＝k2，k2＝
，所以k＝±，x0＝
，故存在点D（，0），使△DGH为等边三角形.
略
） B．（0，－
） D．（0，
）
)50的二项展开式中，整数项共有（ ）项
x0∈R，x
＋1＜0”的否定：
.
，直线l：4x－5y＋40＝0，则椭圆上的点到直线l的距离的最大值为
.
