在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() .
.
⑴求点![]() 的轨迹
的轨迹![]() 的方程.⑵若直线
的方程.⑵若直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 、
、![]() 两点,顺次连接
两点,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 得到的四边形
得到的四边形![]() 是菱形,求
是菱形,求![]() .
.
知识点:5.平面向量
⑴设![]() ,则
,则![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ……4分,化简整理得点
……4分,化简整理得点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
⑵设![]() 、
、![]() ,由
,由![]() 的对称性,得
的对称性,得![]() 、
、![]() ,因为
,因为![]() 是菱形,所以
是菱形,所以![]() ,
,![]() ,即
,即![]() ……9分,由
……9分,由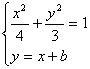 得
得![]() ……10分,
……10分,![]() ,
,![]()
![]()
检验知,此时![]() ……13分,所以
……13分,所以![]()
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴求![]() 的通项公式.⑵证明:对
的通项公式.⑵证明:对![]() ,
,![]() .
.
知识点:3.数列
⑴依题意,![]() ,
,![]() ……1分,
……1分,![]()
所以![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列……3分,所以
的等比数列……3分,所以![]() ,
,![]() .
.
⑵对![]() ,
,![]() ……7分,
……7分,![]() ,所以
,所以![]() ,
,![]()
![]() ……9分,所以
……9分,所以
![]() ……10分,两式相减,整理得
……10分,两式相减,整理得
![]() …11分,
…11分,![]() …13分,
…13分,![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,![]() 是常数.⑴求曲线
是常数.⑴求曲线![]() 在点
在点![]() 处的切线
处的切线![]() .⑵是否存在常数
.⑵是否存在常数![]() ,使
,使![]() 也是曲线
也是曲线![]() 的一条切线.若存在,求
的一条切线.若存在,求![]() 的值;若不存在,简要说明理由.⑶设
的值;若不存在,简要说明理由.⑶设![]() ,讨论函数
,讨论函数![]() 的单调性.
的单调性.
知识点:2.函数概念与基本初等函数Ⅰ
⑴![]() ,
,![]() ,
,![]() ……1分,所以直线
……1分,所以直线![]() 的方程为
的方程为![]() 。
。
⑵设![]() 在
在![]() 处的切线为
处的切线为![]() ,则有
,则有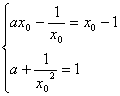 ……4分,解得
……4分,解得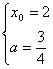 ,即,当
,即,当![]() 时,
时,![]() 是曲线
是曲线![]() 在点
在点![]() 的切线.
的切线.
⑶![]() .
.
当![]() ,
,![]() 时,
时,![]() ……7分,
……7分,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ……9分,
……9分,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调减少;
单调减少;
当![]() 时,解
时,解![]() 得
得![]() ,
,![]() ,
,![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调减少;
单调减少;
当![]() 时,解
时,解![]() 得
得![]() ,
,![]() (
(![]() 舍去)……13分,
舍去)……13分,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调减少.
单调减少.
已知点C(1,0),点A、B是⊙O:![]() 上任意两个不同的点,
上任意两个不同的点,
且满足![]() ,设P为弦AB的中点,
,设P为弦AB的中点,
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线![]() 的距离恰好
的距离恰好
等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
知识点:10.圆锥曲线与方程
解:(1)法一:连结CP,由![]() ,知AC⊥BC
,知AC⊥BC
∴|CP|=|AP|=|BP|=![]() ,由垂径定理知
,由垂径定理知![]()
即![]()
设点P(x,y),有![]() ,化简,得到
,化简,得到![]()
法二:设A![]() ,B
,B![]() ,P
,P![]() ,
,
根据题意,知![]() ,
,![]() ,
,
∴![]()
故![]() ……①
……①
又![]() ,有
,有![]()
∴![]() ,故
,故![]()
代入①式,得到![]() 化简,得到
化简,得到![]()
(2)根据抛物线的定义,到直线![]() 的距离等于到点C(1,0)的距离的点都在抛物线
的距离等于到点C(1,0)的距离的点都在抛物线
![]() 上,其中
上,其中![]() ,∴
,∴![]() ,故抛物线方程为
,故抛物线方程为![]()
![]() 由方程组
由方程组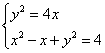 得
得![]() ,解得
,解得![]()
由于![]() ,故取
,故取![]() ,此时
,此时![]() ,
,
故满足条件的点存在的,其坐标为![]() 和
和![]()
已知数列![]() 和
和![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;(2)设
的通项公式;(2)设![]() ,求使得
,求使得![]()
![]() 对一切
对一切![]() 都成立的最小正整数
都成立的最小正整数![]() ;(3)设数列
;(3)设数列![]() 的前
的前![]() 和为
和为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
知识点:3.数列
解:(1)由![]() 得
得![]() 代入
代入![]() 得
得![]() ,
,
整理得![]() ,∵
,∵![]() 否则
否则![]() ,与
,与![]() 矛盾,从而得
矛盾,从而得![]() ,
,
∵ ![]() ∴数列
∴数列![]() 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴![]() ,即
,即![]() .
.
(2)∵![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]() =
=![]()
∴要使![]()
![]() 对一切
对一切![]() 都成立, 必须并且只须满足
都成立, 必须并且只须满足![]() ≤
≤![]() ,即m≥5,
,即m≥5,
∴满足要求的最小正整数![]() 为5.-
为5.-
(3)∵![]()
∴![]() =
=![]()
=![]() -
-
又∵![]()
=![]() =
=![]()
∴![]() .
.
设函数![]() .(1)若
.(1)若![]() ,求函数
,求函数![]() 的极值;(2)若
的极值;(2)若![]() 是函数
是函数![]() 的一个极值点,试求出
的一个极值点,试求出![]() 关于
关于![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ),并确定
),并确定![]() 的单调区间;(3)在(2)的条件下,设
的单调区间;(3)在(2)的条件下,设![]() ,函数
,函数![]() .若存在
.若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
知识点:2.函数概念与基本初等函数Ⅰ
解:(1)∵![]()
![]() 当
当![]() 时,
时,![]()
![]() ,则
,则![]()
![]() -
-
令![]() 得
得![]() ,∵
,∵![]() ∴
∴![]() ,解得
,解得![]() -
-
∵当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时
时![]()
∴当![]() 时,函数
时,函数![]() 有极大值,
有极大值,![]() ,
,
当![]() 时,函数
时,函数![]() 有极小值,
有极小值,![]()
(2)由(1)知![]()
∵![]() 是函数
是函数![]() 的一个极值点 ∴
的一个极值点 ∴![]()
即![]() ,解得
,解得![]()
则![]() =
=![]()
令![]() ,得
,得![]() 或
或![]() ,∵
,∵![]() 是极值点,∴
是极值点,∴![]() ,即
,即![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
综上可知:当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
(3)由(2)知,当a>0时,![]() 在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
在区间(0,1)上的单调递减,在区间(1,4)上单调递增,
∴函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
又∵![]()
![]()
![]() ,
,![]() ,
,
∴函数![]() 在区间[0,4]上的值域是
在区间[0,4]上的值域是![]() ,即
,即![]() -
-
又![]() 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是![]() -
-
∵![]() -
-![]() =
=![]() =
=![]() ,
,
∴存在![]() 使得
使得![]() 成立只须仅须
成立只须仅须
![]() -
-![]() <1
<1![]()
![]() .
.
在平面直角坐标系中,已知向量![]() (
(![]() ),
),![]() ,动点
,动点![]() 的轨迹为T.(1)求轨迹T的方程,并说明该方程表示的曲线的形状;(2)当
的轨迹为T.(1)求轨迹T的方程,并说明该方程表示的曲线的形状;(2)当![]() 时,已知
时,已知![]() 、
、![]() ,试探究是否存在这样的点
,试探究是否存在这样的点![]() :
: ![]() 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
知识点:5.平面向量
解:(1)∵![]() ∴
∴![]() ,得
,得![]() 即
即![]()
当![]() 时,方程表示两条与x轴平行的直线;
时,方程表示两条与x轴平行的直线;
当![]() 时,方程表示以原点为圆心,4为半径的圆;
时,方程表示以原点为圆心,4为半径的圆;
当![]() 且
且![]() 时,方程表示椭圆;
时,方程表示椭圆;
当![]() 时,方程表示双曲线.
时,方程表示双曲线.
(2)由(1)知,当![]() 时,轨迹T的方程为:
时,轨迹T的方程为:![]() .
.
连结OE,易知轨迹T上有两个点A![]() ,B
,B![]() 满足
满足![]() ,
,
分别过A、B作直线OE的两条平行线![]() 、
、![]() .
.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线![]() 、
、![]() 上.
-
上.
-
∵![]() ∴直线
∴直线![]() 、
、![]() 的方程分别为:
的方程分别为:![]() 、
、![]()
设点![]() (
(![]() )∵
)∵![]() 在轨迹T内,∴
在轨迹T内,∴![]()
分别解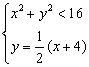 与
与 得
得![]() 与
与![]()
∵![]() ∴
∴![]() 为偶数,在
为偶数,在![]() 上
上![]() ,对应的
,对应的![]()
在![]() 上
上![]() ,对应的
,对应的![]() -
-
∴满足条件的点![]() 存在,共有6个,它们的坐标分别为:
存在,共有6个,它们的坐标分别为:![]()
![]() .
.
已知曲线![]() :
:![]() ,数列
,数列![]() 的首项
的首项![]() ,且当
,且当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上,数列
上,数列![]() 满足
满足![]() .(1)试判断数列
.(1)试判断数列![]() 是否是等差数列?并说明理由;(2)求数列
是否是等差数列?并说明理由;(2)求数列![]() 和
和![]() 的通项公式;(3)设数列
的通项公式;(3)设数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 的前n项和
的前n项和![]() 与2的大小.
与2的大小.
知识点:10.圆锥曲线与方程
解:(1)∵当![]() 时,点
时,点![]() 恒在曲线
恒在曲线![]() 上,∴
上,∴![]() -
-
由![]() 得,当
得,当![]() 时,
时,![]()
![]()
![]()
![]() ---
---
∴数列![]() 是公差为
是公差为![]() 的等差数列.------------------------
的等差数列.------------------------
(2)∵![]() =4,∴
=4,∴![]() ,∴
,∴![]() -
-
由![]() 得
得![]() ----------------------------------
----------------------------------
(3)∵![]() ∴
∴![]() =
=![]() --------------
--------------
∴![]()
![]()
![]() -----14分
-----14分
设函数![]() 。(1)当
。(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)记函数![]() ,若函数
,若函数![]() 有零点,求
有零点,求![]() 的取值范围.
的取值范围.
知识点:2.函数概念与基本初等函数Ⅰ
解:(1)当![]() 时,
时,![]() =
=![]()
∴当![]() 时,
时,![]() ---
---
当![]() 时,
时,![]() =
=![]()
∵函数![]() 在
在![]() 上单调递增 ∴
上单调递增 ∴![]() --------
--------
由![]() 得
得![]() 又
又![]()
![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .-
.-
(2)函数![]() 有零点即方程
有零点即方程![]() 有解,即
有解,即![]() 有解
有解
令![]() 当
当![]() 时
时![]()
∵![]() ,∴函数
,∴函数![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,
,
当![]() 时,
时,![]()
∵![]()
![]()
![]() ------
------
∴函数![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() ---------
---------
∴方程![]() 有解时
有解时![]() ,即函数
,即函数![]() 有零点时
有零点时![]()
如图所示,椭圆![]() 的离心率为
的离心率为![]() ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线![]() ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线![]() 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线![]() 距离的最小值。
距离的最小值。

知识点:10.圆锥曲线与方程
解:(1)由题意可知,![]()
![]() ,即
,即![]()
![]() 所以椭圆C的方程为:
所以椭圆C的方程为:![]()
(2)方法一:由(1)可求得椭圆C的坐标F(1,0)
![]() 抛物线E的方程为:
抛物线E的方程为:![]() ,而直线
,而直线![]() 的方程为
的方程为![]()
![]() 设动点M为
设动点M为![]() ,则点M到直线
,则点M到直线![]() 的距离为
的距离为

即抛物线E上的点到直线![]() 距离的最小值为
距离的最小值为![]()
方法二:由(1)可求得椭圆C的右焦点坐标F(1,0)
![]() 抛物线E的方程为:
抛物线E的方程为:![]() ,而直线
,而直线![]() 的方程为
的方程为![]()
可设与直线![]() 平行且抛物线E相切的直线
平行且抛物线E相切的直线![]() 方程为:
方程为:![]()
由 可得:
可得:![]() 9分
9分![]() ,
,
解得: ![]() 直线
直线![]() 方程为:
方程为:![]()
![]() 抛物线上的点到直线的距离的最小值等于直线
抛物线上的点到直线的距离的最小值等于直线![]() 与
与![]() 的距离:
的距离:![]()
已知![]() 是
是![]() 的导函数,
的导函数,![]() ,且函数
,且函数![]() 的图象过点(0,-2)。(1)求函数
的图象过点(0,-2)。(1)求函数![]() 的表达式;(2)设
的表达式;(2)设![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直,求
轴垂直,求![]() 的极大值。
的极大值。
知识点:11.导数及其应用
解:(1)由已知得![]() 2分
2分
又![]() ,
,![]() 4分,
4分,![]() 5分,
5分,![]()
(2)![]()
![]()
![]()
又![]() ,由
,由![]()
![]() ,
,![]()
由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]()
则![]() 的单调增区间是
的单调增区间是![]() ,单调递减区间是
,单调递减区间是![]()
故![]() 极大值为
极大值为![]()
极小值为![]()
设![]() ,方程
,方程![]() 有唯一解,已知
有唯一解,已知![]() ,且
,且![]()
(1)求数列![]() 的通项公式;(2)若
的通项公式;(2)若![]() ,求和
,求和![]() ;(3)问:是否存在最小整数
;(3)问:是否存在最小整数![]() ,使得对任意
,使得对任意![]() ,有
,有![]() 成立,若存在,求出
成立,若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
知识点:3.数列
解:(1)因为方程![]()
![]() 有唯一解,可求
有唯一解,可求![]() 从而得到
从而得到![]()
![]() ,
,![]() ,
,
又由已知![]()
数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列 4分,故
的等差数列 4分,故![]()
所以数列![]() 的通项公式为
的通项公式为![]()
![]() (2)将
(2)将![]() 代入
代入![]() 可求得
可求得
![]()
![]()
(3)![]() 恒成立,
恒成立,![]() 只要
只要![]() 即可,
即可,
而![]() ,即要
,即要![]() ,
,
故存在最小的正整数![]()
已知椭圆![]() :
:![]() 的面积为
的面积为![]() ,且
,且![]() 包含于平面区域
包含于平面区域![]()
![]() 内,向
内,向![]() 内随机投一点Q,点Q落在椭圆
内随机投一点Q,点Q落在椭圆![]() 内的概率为
内的概率为![]() .(Ⅰ)试求椭圆
.(Ⅰ)试求椭圆![]() 的方程;(Ⅱ)若斜率为
的方程;(Ⅱ)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一点,记直线
上一点,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,试问:
,试问:![]() 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
知识点:1.椭圆
(Ⅰ)平面区域![]()
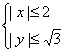 是一个矩形区域,
是一个矩形区域,
如图所示. 依题意及几何概型,可得![]() ,
,
即 ![]() .因为
.因为 ![]() ,
,
所以, ![]() . 所以,椭圆
. 所以,椭圆![]() 的方程为
的方程为![]()
(Ⅱ)设直线![]() 的方程为:
的方程为:![]() ,
,![]()
联立直线![]() 的方程与椭圆方程得:
的方程与椭圆方程得:
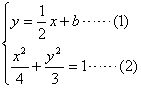
(1)代入(2)得:![]()
化简得:![]() ………(3)
………(3)
当![]() 时,即,
时,即,![]()
也即,![]() 时,直线
时,直线![]() 与椭圆有两交点, 由韦达定理得:
与椭圆有两交点, 由韦达定理得: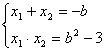 ,
,
所以,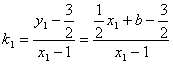 ,
, 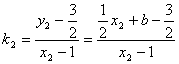
则![]()
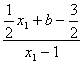
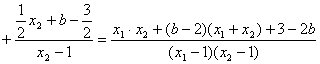
![]() ,所以,
,所以,![]() 为定值。
为定值。
已知数列![]() 满足:
满足:![]() ,且对任意
,且对任意![]() N*都有
N*都有![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;(Ⅱ)求数列
的值;(Ⅱ)求数列![]() 的通项公式;(Ⅲ)证明:
的通项公式;(Ⅲ)证明:![]() =
=![]() (
(![]() N*).
N*).
知识点:3.数列
解:(Ⅰ)由已知,![]()
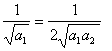 得
得![]() ,
,![]() 得
得![]()
(Ⅱ)当![]() 时,
时,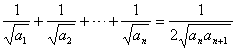 ①
①
![]() ②
②
①-②得:
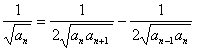 ,
,![]()
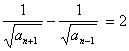
∴ 数列![]() 皆为等差数列,∴
皆为等差数列,∴ ![]()
![]() 综上,
综上, ![]() ,
, ![]()
![]() .
.
(Ⅲ)![]()
![]()
![]() ,
,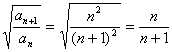 ,∴等式成立。
,∴等式成立。
已知函数![]() .(Ⅰ)判断函数
.(Ⅰ)判断函数![]() 的奇偶性;(Ⅱ)求函数
的奇偶性;(Ⅱ)求函数![]() 的单调区间;(Ⅲ)若关于
的单调区间;(Ⅲ)若关于![]() 的方程
的方程![]() 有实数解,求实数
有实数解,求实数![]() 的取值范围.
的取值范围.
知识点:2.函数概念与基本初等函数Ⅰ
解:(Ⅰ)函数![]() 的定义域为{
的定义域为{![]() 且
且![]() }
}
![]() ,∴
,∴![]() 为偶函数
为偶函数
(Ⅱ)当![]() 时,
时,![]()
若![]() ,则
,则![]() ,
,![]() 递减;若
递减;若![]() , 则
, 则![]() ,
,![]() 递增.
递增.
再由![]() 是偶函数,得
是偶函数,得![]() 的
的
递增区间是![]() 和
和![]() ;递减区间是
;递减区间是![]() 和
和![]() .
.
(Ⅲ)方法一:要使方程![]() 有实数解,即要使函数
有实数解,即要使函数![]() 的图像与直线
的图像与直线![]() 有交点.
有交点.
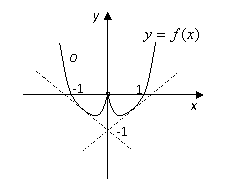 函数
函数![]() 的图象如图.…………………
的图象如图.…………………
先求当直线![]() 与
与![]() 的图象相切时
的图象相切时![]() 的值.
的值.
当![]() 时,
时,![]()
设切点为![]() ,则切线方程为
,则切线方程为
![]() ,将
,将![]() 代入,得
代入,得![]()
即![]() (*)
(*)
显然,![]() 满足(*)而当
满足(*)而当![]() 时,
时,![]() ,当
,当 ![]() 时,
时,![]()
∴(*)有唯一解![]() 此时
此时![]()
再由对称性,![]() 时,
时,![]() 也与
也与![]() 的图象相切,…
的图象相切,…
∴若方程![]() 有实数解,则实数
有实数解,则实数![]() 的取值范围是(-∞,-1]∪[1,+∞).
的取值范围是(-∞,-1]∪[1,+∞).
方法二:由![]() ,得:
,得:![]()
令![]()
![]() ,当
,当![]() ,
,![]()
![]() ,显然
,显然![]()
![]() 时,
时,![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() 时,
时,![]()
又![]() ,
,![]() 为奇函数∴
为奇函数∴![]() 时,
时,![]()
∴![]() 的值域为(-∞,-1]∪[1,+∞) ……
的值域为(-∞,-1]∪[1,+∞) ……
∴若方程![]() 有实数解,则实数
有实数解,则实数![]() 的取值范围是(-∞,-1]∪[1,+∞).
的取值范围是(-∞,-1]∪[1,+∞).
已知中心在原点,长轴在x轴上的椭圆的一个顶点是点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为F1和F2 。 (1)求椭圆方程;(2)点M在椭圆上,求⊿MF1F2面积的最大值;(3)试探究椭圆上是否存在一点P,使
,左、右焦点分别为F1和F2 。 (1)求椭圆方程;(2)点M在椭圆上,求⊿MF1F2面积的最大值;(3)试探究椭圆上是否存在一点P,使![]() ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。
知识点:10.圆锥曲线与方程
解:(Ⅰ)设椭圆方程为![]() .由已知,
.由已知,![]() ,
,![]() ,
,
![]() . 解得
. 解得![]() ,∴所求椭圆方程为
,∴所求椭圆方程为![]()
(Ⅱ)令![]() ,则
,则 ![]()
∵![]() ,故
,故![]() 的最大值为
的最大值为![]() -
-
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() 。
。
(Ⅲ)假设存在一点P, 使![]() ,
,![]() ∴
∴![]() ,
,
∴⊿PF1F2为直角三角形,∴![]() ① ---
① ---
又∵![]() ② -------
② -------
∴②2-①,得 ![]() ∴
∴![]() --------
--------
即![]() =5,但由(1)得
=5,但由(1)得![]() 最大值为
最大值为![]() ,故矛盾,∴不存在一点P, 使
,故矛盾,∴不存在一点P, 使![]()
已知数列![]() 的前n项和是
的前n项和是![]() ,且满足
,且满足![]() (1)求数列
(1)求数列![]() 的通项公式;(2)若数列
的通项公式;(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和Tn ;
的前n项和Tn ;
知识点:3.数列
解:(Ⅰ)由![]() 得,
得,![]()
当![]()
![]() ,
,![]()
![]() ,
,![]() 是以2为公比的等比数列
是以2为公比的等比数列
令n=1得![]()
![]() 的通项公式是
的通项公式是![]()
(Ⅱ)由![]() --
--
![]() ,
,![]()
相减得:![]() -
-
![]()
已知函数![]() .(
.(![]() )(1)当
)(1)当![]() 时,求
时,求![]() 在区间[1,e]上的最大值和最小值;(2)若在区间(1,+∞)上,函数
在区间[1,e]上的最大值和最小值;(2)若在区间(1,+∞)上,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方,求
下方,求![]() 的取值范围.
的取值范围.
知识点:2.函数概念与基本初等函数Ⅰ
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]() ;
;
对于![]() [1,e],有
[1,e],有![]() ,
----3分 ∴
,
----3分 ∴![]() 在区间[1,e]上为增函数,-
在区间[1,e]上为增函数,-
∴![]() -----5分,
-----5分,![]() .
.
(Ⅱ)令![]() ,
,
在区间(1,+∞)上,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方
下方
等价于![]() 在区间(1,+∞)上恒成立
, ---
在区间(1,+∞)上恒成立
, ---
∵![]() -----
-----
① 若![]() ,令
,令![]() ,得
,得![]() ,
,![]() , ---
, ---
当![]() ,即
,即![]() 时,在(
时,在(![]() ,+∞)上有
,+∞)上有![]() ,此时
,此时![]() 在区间(
在区间(![]() ,+∞)上是增函数,
,+∞)上是增函数,
![]() ,
,![]() ∈(
∈(![]() ,+∞),不合题意;
,+∞),不合题意;
当![]() ,即
,即![]() 时,同理可知,
时,同理可知,![]() 在区间(1,+∞)上是增函数,
在区间(1,+∞)上是增函数,
![]() ,有
,有![]() ∈(
∈(![]() ,+∞),也不合题意;
,+∞),也不合题意;
② 若![]() ,则有
,则有![]() ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有![]() ,
,
从而![]() 在区间(1,+∞)上是减函数;
-----
在区间(1,+∞)上是减函数;
-----
要使![]() 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足![]()
![]() ,--13分由此求得
,--13分由此求得![]() 的范围是[
的范围是[![]() ,
,![]() ].
综上述,
].
综上述,![]() 的取值范围是[
的取值范围是[![]() ,
,![]() ].
].
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .(1)求
.(1)求![]() 的值; (2)求数列
的值; (2)求数列![]() 的通项公式
的通项公式![]() ;[来源:学§科§网Z§X§X§K](3)设
;[来源:学§科§网Z§X§X§K](3)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
知识点:3.数列
解:(1)∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
(2)∵![]() ,∴
,∴![]()
![]() ,∴
,∴![]() ,
,![]()
![]()
又![]() ,∴数列
,∴数列![]() 自第
自第![]() 项起是公比为
项起是公比为![]() 的等比数列,∴
的等比数列,∴ ,
,
(3)∵![]() ,∴
,∴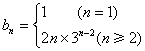 ,
……………
,
……………
∴![]() ,
①
,
①
![]() ② …
② …
①-②得![]()
![]() =
=![]()
∴![]() . …………………………来源:Zxxk.Com]
. …………………………来源:Zxxk.Com]
设函数![]() ,其中
,其中![]() 为常数.(1)证明:对任意
为常数.(1)证明:对任意![]() ,
,![]() 的图象恒过定点;(2)当
的图象恒过定点;(2)当![]() 时,判断函数
时,判断函数![]() 是否存在极值?若存在,证明你的结论并求出所有极值;若不存在,说明理由.
是否存在极值?若存在,证明你的结论并求出所有极值;若不存在,说明理由.
知识点:2.函数概念与基本初等函数Ⅰ
解:(1)令![]() ,得
,得![]() ,且
,且![]() ,[来源:学。科。网] 所以
,[来源:学。科。网] 所以![]() 的图象恒过定点
的图象恒过定点![]() ;
;
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]()
经观察得![]() 有根
有根![]() 令
令![]() ,
,![]()
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是单调递增函数.所以
上是单调递增函数.所以![]() 有唯一根
有唯一根![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数.…
上是增函数.…
所以![]() 是
是![]() 的唯一极小值点.极小值是
的唯一极小值点.极小值是![]() . …
. …
已知抛物线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,直线
,直线![]()
(![]() )是
)是![]() 、
、![]() 的公切线.
的公切线.![]() 是
是![]() 的焦点.(1)求
的焦点.(1)求![]() 与
与![]() 的值;(2)设
的值;(2)设![]() 是
是![]() 上的一动点,以
上的一动点,以![]() 为切点的
为切点的![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() ,证明:点
,证明:点![]() 在一定直线上.
在一定直线上.
知识点:3.抛物线
解:(1)由已知,圆![]() :
: ![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
由题设圆心到直线![]() 的距离
的距离![]() . ……………
. ……………
即![]() ,解得
,解得![]() (
(![]() 舍去). …………………
舍去). …………………
设![]() 与抛物线的相切点为
与抛物线的相切点为![]() ,又
,又![]() ,得
,得![]() ,
,![]() .
.
代入直线方程得:![]() ,∴
,∴![]() 所以
所以![]() ,
,![]() .
.
(2)由(1)知抛物线![]() 方程
方程![]() 为
为![]() ,焦点
,焦点![]() .
.
设![]() ,由(1)知以
,由(1)知以![]() 为切点的切线
为切点的切线![]() 的方程为
的方程为![]() .
.
令![]() ,得切线
,得切线![]() 交
交![]() 轴的
轴的![]() 点坐标为
点坐标为![]()
所以![]() ,
,![]() ,∴
,∴![]()
因为![]() 是定点,所以点
是定点,所以点![]() 在定直线
在定直线![]() 上.
上.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设![]() ,把y表示成
,把y表示成![]() 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?
知识点:14.函数的应用问题
【解】(1)在![]() 中,
中,![]() 所以
所以![]() =OA=
=OA=![]() .所以
.所以![]() 由题意知
由题意知![]() . …
. …
所以点P到A、B、C的距离之和为![]() .
.
故所求函数关系式为![]() .
…………………
.
…………………
(2)由(1)得![]() ,令
,令![]() 即
即![]() ,又
,又![]() ,从而
,从而![]() . .
. .
当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() .
.
所以当![]() 时,
时,![]() 取得最小值, ………
取得最小值, ………
此时![]() (km),即点P在OA上距O点
(km),即点P在OA上距O点![]() km处.
km处.
变电站建于距O点![]() km处时,它到三个小区的距离之和最小. ………
km处时,它到三个小区的距离之和最小. ………
已知椭圆![]() 的离心率为
的离心率为![]() ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且![]() . (1)求椭圆C和直线l的方程;(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线
. (1)求椭圆C和直线l的方程;(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线![]() 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
知识点:1.椭圆
【解】(1)由离心率![]() ,得
,得![]() ,即
,即![]() .
① ………
.
① ………
又点![]() 在椭圆
在椭圆![]() 上,即
上,即![]() .
② …………
.
② …………
解 ①②得![]() ,
,
故所求椭圆方程为![]() .
…………
.
…………
由![]() 得直线l的方程为
得直线l的方程为![]() . …
. …
(2)曲线![]() ,即圆
,即圆![]() ,其圆心坐标为
,其圆心坐标为![]() ,半径
,半径![]() ,表示圆心在直线
,表示圆心在直线![]() 上,半径为
上,半径为![]() 的动圆. ………………… 10分
的动圆. ………………… 10分
由于要求实数m的最小值,由图可知,只须考虑![]() 的情形.
的情形.
设![]() 与直线l相切于点T,则由
与直线l相切于点T,则由![]() ,得
,得![]() ,…
,…
当![]() 时,过点
时,过点![]() 与直线l垂直的直线
与直线l垂直的直线![]() 的方程为
的方程为![]() ,解方程组
,解方程组![]()
得![]() .…………
.…………
因为区域D内的点的横坐标的最小值与最大值分别为![]() , 所以切点
, 所以切点![]() ,由图可知当
,由图可知当![]() 过点B时,m取得最小值,即
过点B时,m取得最小值,即![]() ,解得
,解得![]() . …………
. …………
已知二次函数g(x)对任意实数x都满足![]() ,且
,且![]() .令
.令
![]() .
.
(1)求 g(x)的表达式; (2)若![]() 使
使![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设![]() ,
,![]() ,证明:对
,证明:对![]() ,恒有
,恒有![]()
知识点:2.函数概念与基本初等函数Ⅰ
【解】 (1)设![]() ,于是
,于是![]() 所以
所以
又![]() ,则
,则![]() .所以
.所以![]() .
…………
.
…………
(2)![]()
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,![]() 对
对![]() ,
,![]() 恒成立; ………
恒成立; ………
当m<0时,由![]() ,列表:
,列表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
减 |
极小 |
增 |
![]()
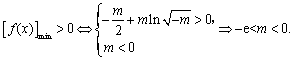
所以若![]() ,
,![]() 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是![]() .
.
故![]() 使
使![]() 成立,实数m的取值范围
成立,实数m的取值范围![]() .………
.………
(3)因为对![]() ,
,![]() 所以
所以![]() 在
在![]() 内单调递减.
内单调递减.
于是![]()
![]() ……
……
记![]() ,则
,则![]()
由于卫生的要求游泳池要经常换水(进一些干净的水同时放掉一些脏水), 游泳池的水深经常变化,已知泰州某浴场的水深![]() (米)是时间
(米)是时间![]() ,(单位小时)的函数,记作
,(单位小时)的函数,记作![]() ,下表是某日各时的水深数据
,下表是某日各时的水深数据
t(时)
0
3
6
9
12
15
18
21
24
y(米)
2![]() 5
5
2![]() 0
0
1![]() 5
5
2![]() 0
0
2![]() 49
49
2
1![]() 51
51
1![]() 99
99
2![]() 5
5
经长期观测的曲线![]() 可近似地看成函数
可近似地看成函数![]()
(Ⅰ)根据以上数据,求出函数![]() 的最小正周期T,振幅A及函数表达式;
的最小正周期T,振幅A及函数表达式;
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,判断一天内的上午8![]() 00至晚上20
00至晚上20![]() 00之间,有多少时间可供游泳爱好者进行运动
00之间,有多少时间可供游泳爱好者进行运动![]()