已知集合A={x|x﹣2<0},B={x|x<a},若A∩B=A,则实数a的取值范围是( )
A.(﹣∞,﹣2]B.[﹣2,+∞)C.(﹣∞,2]D.[2,+∞)
知识点:3.集合的基本运算
D
【分析】化简A,再根据A∩B=A,求得实数a的取值范围.
【解答】解:∵集合A={x|x﹣2<0}={x|x<2},B={x|x<a},A∩B=A,
∴a≥2,
故选:D.
【点评】本题主要考查两个集合的交集的定义和求法,属于基础题.
若复数x满足x+i= ,则复数x的模为( )
,则复数x的模为( )
A. B.10C.4D.
B.10C.4D.
知识点:3.复数代数形式的四则运算
A
【分析】利用复数代数形式的乘除运算求得复数x,再求其模即可.
【解答】解:x+i=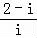 ,
,
∴x=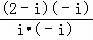 ﹣i=﹣1﹣3i,
﹣i=﹣1﹣3i,
∴|x|=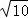 ,
,
故选:A.
【点评】本题考查复数代数形式的乘除运算,属于基础题.
下列函数中,在(0,+∞)上单调递减,并且是偶函数的是( )
A.y=x2B.y=﹣x3C.y=﹣ln|x|D.y=2x
知识点:3.单调性与最大(小)值
C
【分析】本题根据函数奇偶性定义,判断函数的是否为偶函数,再根据函数单调性判断函数是否为减函数,得到本题结论.
【解答】解:选项A,
y=x2是偶函数,
当x>0时,y=x在在(0,+∞)上单调递增,不合题意;
选项B,
y=﹣x3,是奇函数,不合题意;
选项C,
y=﹣ln|x|是偶函数,
当x>0时,y=﹣lnx在在(0,+∞)上单调递减,符合题意;
选项D,
y=2x,不是偶函数,递增,不合题意.
故选:C.
【点评】本题考查了奇偶性与单调性,本题难度不大,属于基础题.
双曲线的一个顶点为(2,0),一条渐近线方程为y= x,则该双曲线的方程是( )
x,则该双曲线的方程是( )
A. ﹣
﹣ =1B.
=1B. ﹣
﹣ =1C.
=1C. ﹣
﹣ =1D.
=1D. ﹣
﹣ =1
=1
知识点:2.双曲线
D
【分析】根据双曲线的一条渐近线方程为y= x,且一个顶点的坐标是(2,0),可确定双曲线的焦点在x轴上,从而可求双曲线的标准方程.
x,且一个顶点的坐标是(2,0),可确定双曲线的焦点在x轴上,从而可求双曲线的标准方程.
【解答】解:∵双曲线的一个顶点为(2,0),
∴其焦点在x轴,且实半轴的长a=2,
∵双曲线的一条渐近线方程为y= x,∴b=2
x,∴b=2 ,
,
∴双曲线的方程是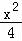 ﹣
﹣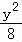 =1.
=1.
故选:D.
【点评】本题考查双曲线的简单性质,判断焦点位置与实半轴的长是关键,属于中档题.
下列说法中不正确的个数是( )
①命题“∀x∈R,x3﹣x2+1≤0”的否定是“∃x0∈R,x03﹣x02+1>0”;
②若“p∧q”为假命题,则p、q均为假命题;
③“三个数a,b,c成等比数列”是“b= ”的既不充分也不必要条件.
”的既不充分也不必要条件.
A.OB.1C.2D.3
知识点:7.全称量词与存在量词
B
【分析】①根据含有量词的命题的否定判断.②根据复合命题与简单命题之间的关系判断.③根据充分条件和必要条件的定义判断.
【解答】解:①全称命题的否定是特称命题,∴命题“∀x∈R,x3﹣x2+1≤0”的否定是“∃x0∈R,x03﹣x02+1>0”正确.
②若“p∧q”为假命题,则p、q至少有一个为假命题;故错误.
③“三个数a,b,c成等比数列”则b2=ac,∴b= ,
,
若a=b=c=0,满足b=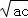 ,但三个数a,b,c成等比数列不成立,
,但三个数a,b,c成等比数列不成立,
∴“三个数a,b,c成等比数列”是“b=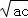 ”的既不充分也不必要条件,正确.
”的既不充分也不必要条件,正确.
故不正确的是②.
故选:B.
【点评】本题主要考查命题的真假判断,解决的关键是对于命题的否定以及真值的判定的运用,属于基础题
已知直线l⊥平面α,直线m⊂平面β,给出下列命题
①α∥β=l⊥m;
②α⊥β⇒l∥m;
③l∥m⇒α⊥β;
④l⊥m⇒α∥β.
其中正确命题的序号是( )
A.①②③B.②③④C.①③D.②④
知识点:4.空间点、直线、平面之间的位置关系
C
【分析】由两平行平面中的一个和直线垂直,另一个也和平面垂直得直线l⊥平面β,再利用面面垂直的判定可得①为真命题;
当直线与平面都和同一平面垂直时,直线与平面可以平行,也可以在平面内,故②为假命题;
由两平行线中的一条和平面垂直,另一条也和平面垂直得直线m⊥平面α,再利用面面垂直的判定可得③为真命题;
当直线与平面都和同一平面垂直时,直线与平面可以平行,也可以在平面内,如果直线m在平面α内,则有α和β相交于m,故④为假命题.
【解答】解:l⊥平面α且α∥β可以得到直线l⊥平面β,又由直线m⊂平面β,所以有l⊥m;即①为真命题;
因为直线l⊥平面α且α⊥β可得直线l平行与平面β或在平面β内,又由直线m⊂平面β,所以l与m,可以平行,相交,异面;故②为假命题;
因为直线l⊥平面α且l∥m可得直线m⊥平面α,又由直线m⊂平面β可得α⊥β;即③为真命题;
由直线l⊥平面α以及l⊥m可得直线m平行与平面α或在平面α内,又由直线m⊂平面β得α与β可以平行也可以相交,即④为假命题.
所以真命题为①③.
故选 C.
【点评】本题是对空间中直线和平面以及直线和直线位置关系的综合考查.重点考查课本上的公理,定理以及推论,所以一定要对课本知识掌握熟练,对公理,定理以及推论理解透彻,并会用.
记定义在区间[a,b]上的连续函数y=f(x),如果存在x0∈[a,b],使得f(x0)= 成立,则称x0为函数f(x)在[a,b]上的“平均值点”,那么函数f(x)=x3+2x在[﹣1,1]上“平均值点”的个数为( )
成立,则称x0为函数f(x)在[a,b]上的“平均值点”,那么函数f(x)=x3+2x在[﹣1,1]上“平均值点”的个数为( )
A.1B.2C.3D.4
知识点:6.微积分的基本定理
A
【分析】由新定义计算定积分可将问题转化为g(x)=x3+2x﹣ 在x∈[﹣1,1]上的零点个数,由零点判定定理和函数单调性可得.
在x∈[﹣1,1]上的零点个数,由零点判定定理和函数单调性可得.
【解答】解:由题意可得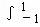 (x3+2x)dx=(
(x3+2x)dx=(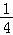 x4+x2)
x4+x2)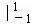 =
=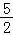 ,
,
∴函数f(x)=x3+2x在[﹣1,1]上“平均值点”的个数为方程x3+2x= 在[﹣1,1]上根的个数,
在[﹣1,1]上根的个数,
构造函数g(x)=x3+2x﹣ ,则问题转化为g(x)在x∈[﹣1,1]上的零点个数,
,则问题转化为g(x)在x∈[﹣1,1]上的零点个数,
求导数可得g′(x)=3x2+2>0,故函数g(x)在x∈[﹣1,1]上单调递增,
由g(﹣1)g(1)<0,故函数g(x)在x∈[﹣1,1]上有唯一一个零点.
故选:A.
【点评】本题考查定积分的运算,涉及转化和数形结合的思想,属中档题.
(5分)(2016呼伦贝尔一模)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n个这样的几何体拼成一个棱长为4的正方体,则V,n的值是( )

A.V=32,n=2B. C.
C. D.V=16,n=4
D.V=16,n=4
知识点:2.空间几何体的三视图和直观图
B
【分析】由三视图可知,几何体为底面是正方形的四棱锥,再根据公式求解即可.
【解答】解:由三视图可知,几何体为底面是正方形的四棱锥,
所以V=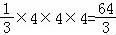 ,
,
边长为4的正方体V=64,所以n=3.
故选B
【点评】本题考查学生的空间想象能力,是基础题.
(5分)(2016漳州一模)已知曲线f(x)=sin(wx)+ cos(wx)(w>0)的两条相邻的对称轴之间的距离为
cos(wx)(w>0)的两条相邻的对称轴之间的距离为 ,且曲线关于点(x0,0)成中心对称,若x0∈[0,
,且曲线关于点(x0,0)成中心对称,若x0∈[0, ],则x0=( )
],则x0=( )
A. B.
B. C.
C. D.
D.
知识点:7.函数y=Asin(wx+@)+B
C
【分析】利用两角和的正弦公式化简f(x),然后由f(x0)=0求得[0,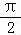 ]内的x0的值.
]内的x0的值.
【解答】解:∵曲线f(x)=sin(wx)+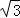 cos(wx)=2sin(wx+
cos(wx)=2sin(wx+ )的两条相邻的对称轴之间的距离为
)的两条相邻的对称轴之间的距离为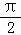 ,
,
∴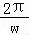 =π,
=π,
∴w=2
∴f(x)=2sin(2x+ ).
).
∵f(x)的图象关于点(x0,0)成中心对称,
∴f(x0)=0,即2sin(2x0+ )=0,
)=0,
∴2x0+ =kπ,
=kπ,
∴x0=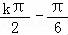 ,k∈Z,
,k∈Z,
∵x0∈[0,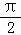 ],
],
∴x0= .
.
故选:C.
【点评】本题考查两角和与差的正弦函数,考查了正弦函数的对称中心的求法,是基础题.
已知在三棱锥P﹣ABC中,PA=PB=BC=1,AB= ,AB⊥BC,平面PAB⊥平面ABC,若三棱锥的顶点在同一个球面上,则该球的表面积是( )
,AB⊥BC,平面PAB⊥平面ABC,若三棱锥的顶点在同一个球面上,则该球的表面积是( )
A. πB.3πC.
πB.3πC. D.2π
D.2π
知识点:11.球
B
【分析】求出P到平面ABC的距离为 ,AC为截面圆的直径,AC=
,AC为截面圆的直径,AC=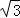 ,由勾股定理可得R2=(
,由勾股定理可得R2=(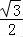 )2+d2=(
)2+d2=( )2+(
)2+(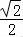 ﹣d)2,求出R,即可求出球的表面积.
﹣d)2,求出R,即可求出球的表面积.
【解答】解:由题意,AC为截面圆的直径,AC=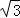 ,
,
设球心到平面ABC的距离为d,球的半径为R,
∵PA=PB=1,AB=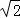 ,
,
∴PA⊥PB,
∵平面PAB⊥平面ABC,
∴P到平面ABC的距离为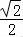 .
.
由勾股定理可得R2=(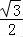 )2+d2=(
)2+d2=( )2+(
)2+(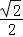 ﹣d)2,
﹣d)2,
∴d=0,R2=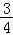 ,
,
∴球的表面积为4πR2=3π.
故选:B.
【点评】本题考查球的表面积,考查学生的计算能力,求出球的半径是关键.
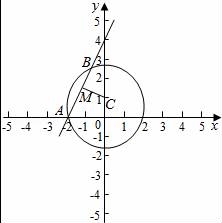
在平面直角坐标系xOy中,已知⊙C:x2+(y﹣1)2=5,点A为⊙C与x轴负半轴的交点,过A作⊙C的弦AB,记线段AB的中点为M,若|OA|=|OM|,则直线AB的斜率为( )
A.﹣2B. C.2D.4
C.2D.4
知识点:4.直线与圆的位置关系
C
【分析】因为圆的半径为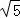 ,所以A(﹣2,0),连接CM,则CM⊥AB,求出圆的直径,在三角形OCM中,利用正弦定理求出sin∠OCM,利用∠OCM与∠OAM互补,即可得出结论.
,所以A(﹣2,0),连接CM,则CM⊥AB,求出圆的直径,在三角形OCM中,利用正弦定理求出sin∠OCM,利用∠OCM与∠OAM互补,即可得出结论.
【解答】解:因为圆的半径为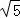 ,所以A(﹣2,0),连接CM,由题意CM⊥AB,
,所以A(﹣2,0),连接CM,由题意CM⊥AB,
因此,四点C,M,A,O共圆,且AC就是该圆的直径,2R=AC=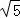 ,
,
在三角形OCM中,利用正弦定理得2R=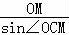 ,
,
根据题意,OA=OM=2,
所以,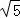 =
=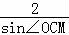 ,
,
所以sin∠OCM= ,tan∠OCM=﹣2(∠OCM为钝角),
,tan∠OCM=﹣2(∠OCM为钝角),
而∠OCM与∠OAM互补,
所以tan∠OAM=2,即直线AB的斜率为2.
故选:C.
【点评】本题考查直线与圆的位置关系,考查正弦定理,考查学生的计算能力,属于中档题.
已知函数f(x)=x3﹣x2﹣x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
A.(﹣∞,﹣1)∪(﹣ ,+∞)B.(﹣
,+∞)B.(﹣ ,1)C.(﹣∞,1)D.(﹣∞,﹣
,1)C.(﹣∞,1)D.(﹣∞,﹣ )∪(1,+∞)
)∪(1,+∞)
知识点:3.导数在研究函数中的应用
D
【分析】求出导数,求出单调区间,求出极值,曲线f(x)与x轴仅有一个交点,可转化成f(x)极大值<0或f(x)极小值>0即可.
【解答】解:函数f(x)=x3﹣x2﹣x+a的导数为f′(x)=3x2﹣2x﹣1,
当x>1或x<﹣ 时,f′(x)>0,f(x)递增;
时,f′(x)>0,f(x)递增;
当﹣ <x<1时,f′(x)<0,f(x)递减.
<x<1时,f′(x)<0,f(x)递减.
即有f(1)为极小值,f(﹣ )为极大值.
)为极大值.
∵f(x)在(﹣∞,﹣ )上单调递增,
)上单调递增,
∴当x→﹣∞时,f(x)→﹣∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞,
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点.
即a+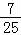 <0或a﹣1>0,
<0或a﹣1>0,
∴a∈(﹣∞,﹣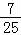 )∪(1,+∞),
)∪(1,+∞),
故选:D.
【点评】本题主要考查了利用导数研究函数的极值,以及函数的单调性,属于中档题.
若| |=1,|
|=1,| |=
|= ,
, ,且
,且 ,则向量
,则向量 与
与 的夹角为 .
的夹角为 .
知识点:4.平面向量的数量积(夹角、模)
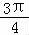
【分析】根据向量的数量积运算和向量的夹角公式即可求出.
【解答】解:设向量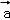 与
与 的夹角为θ,
的夹角为θ,
∵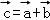 ,且
,且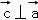 ,
,
∴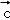
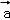 =(
=(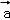 +
+ )
)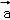 =
=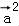 +
+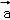
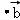 =|
=|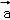 |2+|
|2+|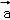 ||
||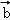 |cosθ=0,
|cosθ=0,
即1+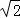 cosθ=0,
cosθ=0,
即cosθ=﹣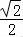 ,
,
∵0≤θ≤π
∴θ= ,
,
故答案为: .
.
【点评】本题考查了向量的数量积运算和向量模的计算,属于基础题.
已知在等差数列{an}中,a1,a2017为方程x2﹣10x+16=0的两根,则a2+a1009+a2016的值为 .
知识点:2.等差数列及其性质
15
【分析】利用一元二次方程的根与系数的关系可得a1+a2017=10再利用等差数列的性质即可得出.
【解答】解:∵a1,a2017为方程x2﹣10x+16=0的两根,
∴a1+a2017=10=2a1009,
∵数列{an}是等差数列,
则a2+a1009+a2016=3a1009=15.
故答案为:15.
【点评】本题考查了一元二次方程的根与系数的关系、等差数列的性质,考查了推理能力与计算能力,属于中档题.
设变量x,y满足约束条件 ,目标函数z=abx+y(a,b均大于0)的最大值为8,则a+b的最小值为 .
,目标函数z=abx+y(a,b均大于0)的最大值为8,则a+b的最小值为 .
知识点:3.二元一次不等式(组)与简单的线性规划
2
【分析】本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再根据目标函数z=abx+y(a>0,b>0)的最大值为8,求出a,b的关系式,再利用基本不等式求出a+b的最小值.
【解答】解:满足约束条件的区域是一个四边形,如下图:

4个顶点是(0,0),(0,2),( ,0),(2,6),
,0),(2,6),
由图易得目标函数在(2,6)取最大值8,
即8=2ab+6,∴ab=1,
∴a+b≥2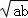 =2,在a=b=2时是等号成立,
=2,在a=b=2时是等号成立,
∴a+b的最小值为2.
故答案为:2.
【点评】用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.
已知F1,F2是椭圆 =1的两个焦点,A,B分别是该椭圆的左顶点和上顶点,点P在线段AB上,则
=1的两个焦点,A,B分别是该椭圆的左顶点和上顶点,点P在线段AB上,则 的最小值为 .
的最小值为 .
知识点:4.平面向量的数量积(夹角、模)
﹣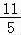
【分析】求得椭圆的焦点和A,B的坐标,以及直线AB的方程,设出P(m,n),求得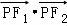 的坐标表示,由m2+n2的几何意义:表示原点与AB上的点的距离的平方,运用点到直线的距离公式即可得到所求最小值.
的坐标表示,由m2+n2的几何意义:表示原点与AB上的点的距离的平方,运用点到直线的距离公式即可得到所求最小值.
【解答】解∵椭圆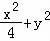 =1,
=1,
∴A(﹣2,0),B(0,1),F1(﹣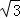 ,0),F2(
,0),F2(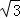 ,0),
,0),
可得AB的方程为x﹣2y+2=0,
设P(m,n),
则 =(﹣
=(﹣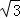 ﹣m,﹣n)(
﹣m,﹣n)(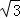 ﹣m,﹣n)
﹣m,﹣n)
=m2+n2﹣3,
由m2+n2的几何意义:表示原点与AB上的点的距离的平方.
可得原点到直线AB的距离取得最小,且为 =
= ,
,
即有m2+n2﹣3的最小值为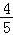 ﹣3=﹣
﹣3=﹣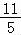 .
.
故答案为:﹣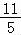 .
.
【点评】本题考查椭圆方程和性质,考查向量的坐标表示及最值的求法,解题时要认真审题,注意m2+n2的几何意义的合理运用,属于中档题.
(12分)(2016大庆一模)已知等比数列{an}的各项均为正数,且a1+2a2=1,a =4a2a6.
=4a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log2a1+log2a2+…+log2an,求数列{ }的前n项和.
}的前n项和.
知识点:5.等比数列的前n项和
【分析】(1)设数列{an}的公比为q,通过解方程组可求得a1与q,从而可求数列{an}的通项公式;
(2)可知{bn}为等差数列,利用等差数列的求和公式可求得bn,利用裂项法,可求数列{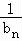 }的前n项和.
}的前n项和.
【解答】解:(1)设等比数列{an}的公比为q,由a =4a2a6得a
=4a2a6得a =4
=4 ,
,
∴q2= ,由已知an>0,∴q=
,由已知an>0,∴q= ,
,
由a1+2a2=1,得2a1=1,∴a1= ,
,
∴数列{an}的通项公式为an= .
.
(2)bn=log2a1+log2a2+…+log2an=﹣(1+2+…+n)=﹣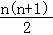
∴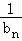 =
=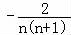 =﹣2(
=﹣2(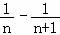 ),
),
∴数列{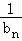 }的前n项和=﹣2[(1﹣
}的前n项和=﹣2[(1﹣ )+(
)+(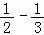 )+…+(
)+…+(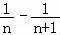 )]=﹣
)]=﹣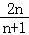 .
.
【点评】本题考查学生灵活运用等比数列的通项公式化简求值,掌握对数的运算性质及等差数列的前n项和的公式,会进行数列的求和运算,是一道中档题.
(12分)(2016大庆一模)已知△ABC的内角A,B,C的对边分别为a,b,c, =(
=( ,c﹣2b),
,c﹣2b), =(sin2C,1),且满足
=(sin2C,1),且满足 =0.
=0.
(1)求∠A的大小;
(2)若a=1,求△ABC周长的取值范围.
知识点:4.平面向量的数量积(夹角、模)
【分析】( I)由已知及平面向量数量积的运算可得2acosC+c﹣2b=0,由余弦定理整理得b2+c2﹣a2=bc,可求cosA= ,结合范围0<A<π,即可解得A的值.
,结合范围0<A<π,即可解得A的值.
( II)由正弦定理及恒等变换的应用可得△ABC的周长l=a+b+c=1+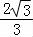 (sinB+sinC)=2sin(B+
(sinB+sinC)=2sin(B+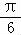 )+1,结合范围0<B<
)+1,结合范围0<B< ,可求
,可求 <sin(B+
<sin(B+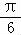 )≤1,即可得解周长的取值范围.
)≤1,即可得解周长的取值范围.
【解答】(本小题满分12分)
解:( I)∵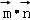 =0,∴
=0,∴ sin2C+c﹣2b=,…(2分)
sin2C+c﹣2b=,…(2分)
∴ ,即2acosC+c﹣2b=0,…(3分)
,即2acosC+c﹣2b=0,…(3分)
由余弦定理得:2a +c﹣2b=0,…(4分)
+c﹣2b=0,…(4分)
整理得b2+c2﹣a2=bc,∴cosA= ,∵0<A<π,∴A=
,∵0<A<π,∴A=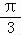 .…(6分)
.…(6分)
( II)∵cosA= ,∴sinA=
,∴sinA=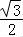 ,…(7分)
,…(7分)
由正弦定理得: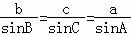 =
=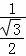 =
=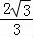 ,…(8分)
,…(8分)
△ABC的周长l=a+b+c=1+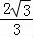 (sinB+sinC)=1+
(sinB+sinC)=1+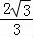 [sinB+sin(B+
[sinB+sin(B+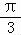 )]
)]
=2sin(B+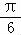 )+1,…(10分)
)+1,…(10分)
∵0<B<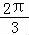 ,∴
,∴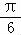 <B
<B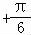 <
< ,∴
,∴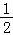 <sin(B+
<sin(B+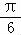 )≤1,…(11分)
)≤1,…(11分)
因此2<l≤3,故△ABC周长的取值范围为(2,3].…(12分)
【点评】本题主要考查了平面向量数量积的运算,正弦定理,余弦定理,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想和数形结合思想的应用,考查了计算能力,属于中档题.
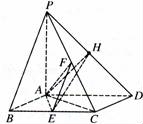
(12分)(2016大庆一模)如图,四棱锥P﹣ABCD的底面是菱形,PA⊥平面ABCD,AC=BC,E,F分别是BC,PC的中点.
(1)证明:平面AEF⊥平面PAD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ,求二面角F﹣AE﹣B的余弦值.
,求二面角F﹣AE﹣B的余弦值.

知识点:10.空间角与距离
【分析】(1)根据面面垂直的判定定理即可得到结论.
(2)建立坐标系,求出平面的法向量,利用向量法进行求解即可.
【解答】解:(1)由四边形ABCD是菱形,AC=BC,可得△ABC为正三角形.∴AE⊥BC.
又∵BC∥AD,∴AE⊥AD …(1分)
∵PA⊥平面ABCD,AE⊂平面ABCD,∴PA⊥AE,
∵PA⊂平面PAD,AD⊂平面PAD,且PA∩AD=A,
∴AE⊥平面PAD,而AE⊂平面AEF,
∴平面AEF⊥平面PAD.…(4分)
(2)设AB=2,H为PD上任意一点,连接AH,EH,
由(I)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.…(5分)
在Rt△EHA中,AE=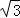 ,∴当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大,此时tan∠EHA=
,∴当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大,此时tan∠EHA= .…(6分)
.…(6分)
∴AH=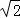 ,又AD=2,∴∠ADH=45°,∴PA=2.…(8分)
,又AD=2,∴∠ADH=45°,∴PA=2.…(8分)
由(I)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系.
又E,F分别是BC,PC的中点,∴A(0,0,0),B(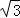 ,﹣1,0),C(
,﹣1,0),C(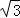 ,1,0),
,1,0),
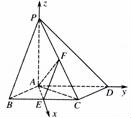
D(0,2,0),P(0,0,2),E(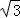 ,0,0),F(
,0,0),F( ,
, ,1).…(9分)
,1).…(9分)
∴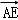 =(
=(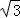 ,0,0),
,0,0),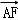 =(
=( ,
, ,1)..
,1)..
设平面AEF的法向量为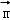 =(x,y,z),
=(x,y,z),
则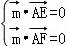 ,∴
,∴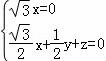 …(10分)
…(10分)
取z=﹣1,则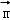 =(0,2,﹣1),为平面AEF的一个法向量.
=(0,2,﹣1),为平面AEF的一个法向量.
又PA⊥平面ABC,∴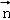 =(0,0,1)为平面ABE的一个法向量.
=(0,0,1)为平面ABE的一个法向量.
∴cos<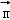 ,
,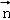 >=
>=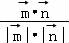 =
=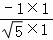 =
=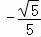 ,
,
故所求二面角的余弦值为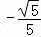 .…(12分)
.…(12分)
【点评】本题主要考查面面垂直判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.
(12分)(2016大庆一模)已知函数f(x)=ln(x+a)﹣x2﹣x在x=0处取得极值.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=﹣ x+b在区间(0,2)有两个不等实根,求实数b的取值范围;
x+b在区间(0,2)有两个不等实根,求实数b的取值范围;
(3)对于n∈N+,证明: .
.
知识点:3.导数在研究函数中的应用
【分析】(1)求导,f′(0)=0,求得a的值,写出函数及导函数表达式,f′(x)>0,求得f(x)的单调递增区间,;由f′(x)<0,求得函数单调递减区间;
(2)构造辅助函数g(x)=f(x)﹣(﹣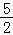 x+b),求导,令g′(x)=0,求得x的值,即可求得g(x)的单调区间,求得g(x)的两个零点,实数b的取值范围;
x+b),求导,令g′(x)=0,求得x的值,即可求得g(x)的单调区间,求得g(x)的两个零点,实数b的取值范围;
(3)由(1)可知当x≥0时ln(x+1)≤x2+x(当且仅当x=0时等号成立),可得到ln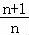 <
<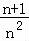 ,求得前n项不等式,采用累加法及对数函数的性质,即可证明不等式成立.
,求得前n项不等式,采用累加法及对数函数的性质,即可证明不等式成立.
【解答】解:(1)由已知得f′(x)=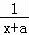 ﹣2x﹣1=
﹣2x﹣1=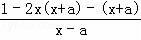 ,…(1分)
,…(1分)
∵f′(0)=0,∴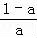 =0,
=0,
∴a=1.
∴f(x)=ln(x+1)﹣x2﹣x(x>﹣1),…(2分)
于是f′(x)=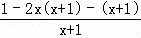 =
= (x>﹣1),
(x>﹣1),
由f′(x)>0得﹣1<x<0;由f′(x)<0,得x>0,
∴f(x)的单调递增区间是(﹣1,0),单调递减区间是(0,+∞).…(4分)
(2)令g(x)=f(x)﹣(﹣ x+b)=ln(x+1)﹣x2+
x+b)=ln(x+1)﹣x2+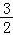 x﹣b,x∈(0,2),
x﹣b,x∈(0,2),
则g′(x)=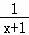 ﹣2x+
﹣2x+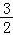 =﹣
=﹣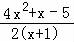 ,令g′(x)=0,得x=1或x=﹣
,令g′(x)=0,得x=1或x=﹣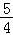 (舍),
(舍),
当0<x<1时,g′(x)>0;当1<x<2时g′(x)<0,即g(x)在(0,1)上单调递增,在(1,2)上单调递减.…(7分)
方程f(x)=﹣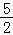 x+b在区间(0,2)有两个不等实根等价于函数g(x)在(0,2)上有两个不同的零点.
x+b在区间(0,2)有两个不等实根等价于函数g(x)在(0,2)上有两个不同的零点.
∴ ,即
,即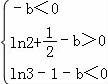 亦即
亦即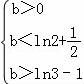 ,
,
∴ln3﹣1<b<ln2+ ,
,
故所求实数b的取值范围为{b丨ln3﹣1<b<ln2+ }.…(9分)
}.…(9分)
证明:(3)由(1)可得,当x≥0时ln(x+1)≤x2+x(当且仅当x=0时等号成立),
设x=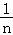 ,则ln(1+
,则ln(1+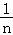 )<
)<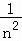 +
+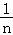 ,即ln
,即ln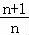 <
<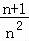 ①…(10分)
①…(10分)
∴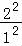 >ln
>ln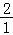 ,
,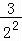 >ln
>ln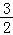 ,
,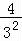 >ln
>ln ,…,
,…,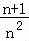 >ln
>ln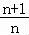 ,
,
将上面n个式子相加得:
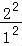 +
+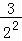 +
+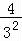 +…+
+…+ >ln
>ln +ln
+ln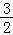 +ln
+ln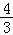 +…+ln
+…+ln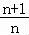 =ln(n+1),
=ln(n+1),
故: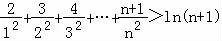 .…(12分)
.…(12分)
【点评】本题考查了利用导数研究函数的单调性极值与最值、方程的实数根转化为函数图象与x轴的交点的问题,同时考查了利用构造函数法证明不等式,考查了推理能力与计算能力,是一道综合题,属于难题.
(12分)(2016大庆一模)从抛物线G:x2=2py(p为常数且p>0)外一点P引抛物线G的两条切线PA和PB(切点为A、B),分别与x轴相交于点C、D,若AB与y轴相交于点Q.
(1)求证:四边形PCQD是平行四边形;
(2)四边形PCQD能否为矩形?若能,求出点Q的坐标;若不能,请说明理由.
知识点:3.抛物线
【分析】(I)设A,B的坐标,求出切线PA,PB的方程,解出P点坐标,设Q坐标和直线AB方程,联立方程组得出P,Q点的坐标关系证明CD平分PQ,求出C,D坐标,得出CD的中点,代入PQ方程即可得出PQ平分CD,于是得出结论;
(II)若四边形PCQD能否为矩形,则|PQ|=|CD|,列方程解出p,t的关系得出Q坐标.
【解答】解:(I)由x2=2py得y=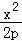 ,∴y′=
,∴y′=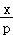 .
.
设A(x1,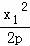 ),B(x2,
),B(x2,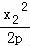 ),则直线PA的方程为y﹣
),则直线PA的方程为y﹣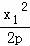 =
=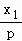 (x﹣x1),①
(x﹣x1),①
直线PB的方程为y﹣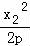 =
=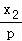 (x﹣x2),②
(x﹣x2),②
由①、②解得x=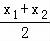 ,y=
,y=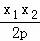 ,∴P点坐标为(
,∴P点坐标为(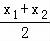 ,
,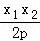 ).
).
设点Q(0,t),则直线AB的方程为y=kx+t.
由 得x2﹣2pkx﹣2pt=0,则x1+x2=2pk,x1x2=﹣2pt,
得x2﹣2pkx﹣2pt=0,则x1+x2=2pk,x1x2=﹣2pt,
∴P(pk,﹣t),∴线段PQ被x轴平分,即被线段CD平分.
在①中,令y=0,解得x=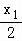 ,∴C(
,∴C(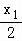 ,0);同理得D(
,0);同理得D(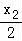 ,0),
,0),
∴线段CD的中点坐标为(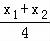 ,0),即(
,0),即( ,0).
,0).
又∵直线PQ的方程为y=﹣ x+t,∴线段CD的中点(
x+t,∴线段CD的中点( ,0)在直线PQ上,即线段CD被线段PQ平分,
,0)在直线PQ上,即线段CD被线段PQ平分,
∴四边形PCQD是平行四边形.
(II)若四边形PCQD是矩形,则|PQ|=|CD|,即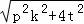 =
=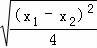 =
=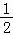
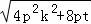 ,解得t=
,解得t= .
.
∴当点Q为(0, )(即抛物线G的焦点)时,四边形PCQD为矩形.
)(即抛物线G的焦点)时,四边形PCQD为矩形.
【点评】本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.
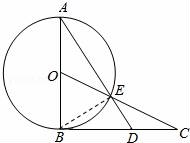
(10分)(2016大庆一模)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
(1)求证:CE2=CDCB;
(2)若AB=BC=2,求CE和CD的长.

知识点:1.几何证明选讲
【分析】(1)要证CE2=CDCB,结合题意,只需证明△CED∽△CBE即可,故连接BE,利用弦切角的知识即可得证;
(2)在Rt三△OBC中,利用勾股定理即可得出CE的长,由(1)知,CE2=CDCB,代入CE即可得出CD的长.
【解答】(1)证明:连接BE.
∵BC为⊙O的切线∴∠ABC=90°
∵AB为⊙O的直径∴∠AEB=90° …(2分)
∴∠DBE+∠OBE=90°,∠AEO+∠OEB=90°
∵OB=OE,∴∠OBE=∠OEB∴∠DBE=∠AEO …(4分)
∵∠AEO=∠CED∴∠CED=∠CBE,
∵∠C=∠C∴△CED∽△CBE,
∴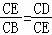 ,∴CE2=CDCB …(6分)
,∴CE2=CDCB …(6分)
(2)解:∵OB=1,BC=2,∴OC=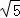 ,∴CE=OC﹣OE=
,∴CE=OC﹣OE=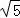 ﹣1 …(8分)
﹣1 …(8分)
由(1)CE2=CDCB得:(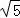 ﹣1)2=2CD,∴CD=3﹣
﹣1)2=2CD,∴CD=3﹣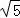 …(10分)
…(10分)
【点评】本题主要考查了切线的性质及其应用,同时考查了相似三角形的判定和解直角三角形等知识点,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
(2016大庆一模)在平面直角坐标系xOy中,直线l的参数方程为 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=2
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=2 sinθ.
sinθ.
(I)求出直线l的普通方程与曲线C的直角坐标方程;
(II)设直线l与曲线C的交点为A,B,求|AB|的值.
知识点:2.坐标系与参数方程
【分析】(1)使用加减消元法消去参数t即得直线l的普通方程,将极坐标方程两边同乘ρ即可得到曲线C的直角坐标方程;
(2)求出曲线C的圆心到直线l的距离,利用垂径定理求出|AB|.
【解答】解:(I)∵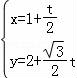 (t为参数),∴
(t为参数),∴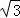 x﹣y=
x﹣y=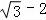 ,
,
即直线l的普通方程为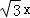 ﹣y+2﹣
﹣y+2﹣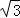 =0.
=0.
由ρ=2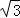 sinθ得ρ2=2
sinθ得ρ2=2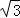 ρsinθ,即x2+y2=2
ρsinθ,即x2+y2=2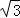 y.
y.
∴曲线C的直角坐标方程为x2+y2=2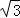 y.即x2+(y﹣
y.即x2+(y﹣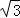 )2=3.
)2=3.
(II)由(1)知曲线C的圆心为(0,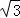 ),半径r=
),半径r=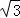 .
.
∴曲线C的圆心到直线l的距离d=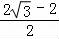 =
=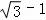 .
.
∴|AB|=2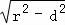 =2
=2 =2
=2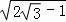 .
.
【点评】本题考查了参数方程,极坐标方程与普通方程的转化,直线与圆的位置关系,属于基础题.
(2016大庆一模)设函数f(x)=|2x﹣1|﹣|x+2|.
(1)解不等式:f(x)>0;
(2)若f(x)+3|x+2|≥|a﹣1|对一切实数x均成立,求a的取值范围.
知识点:3.不等式选讲
【分析】(1)需要去掉绝对值,得到不等式解得即可,
(2)把含所有绝对值的函数,化为分段函数,再根据函数f(x)有最小值的充要条件,即可求得.
【解答】解:(1)f(x)=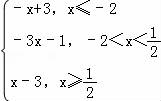 ,
,
当x≤﹣2时,由f(x)>0得﹣x+3>0,解得x≤﹣2,
当﹣2<x< 时,由f(x)>0得﹣3x﹣1>0,解得﹣2<x<﹣
时,由f(x)>0得﹣3x﹣1>0,解得﹣2<x<﹣ ,
,
当x≥ 时,由f(x)>0得x﹣3>0,解得x>3,
时,由f(x)>0得x﹣3>0,解得x>3,
综上,得f(x)>0的解集为{x|x<﹣ 或x>3};
或x>3};
(2)∵f(x)+3|x+2|=|2x﹣1|+2|x+2|=|1﹣2x|+|2x+4|≥|(1﹣2x)+(2x+4)|=5,
∴由题意可知|a﹣1|≤5,解得﹣4≤a≤6,
故所求a的取值范围是{a|﹣4≤a≤6}.
【点评】本题主要考查含有绝对值不等式的解法,关键是去绝对值,需要分类讨论,属于中档题.