设集合A={x|x>a},集合B={x|x2﹣2x﹣15<0},若B∩(∁RA)≠∅,则实数a的取值范围是( )
A.a≤﹣3 B.a>﹣3 C.﹣3<a<5 D.a≥5
知识点:3.集合的基本运算
B
【考点】集合关系中的参数取值问题.
【专题】计算题;探究型.
【分析】先化简集合B,然后利用B∩(∁RA)≠∅,求实数a的取值范围.
【解答】解:集合B={x|x2﹣2x﹣15<0}={x|﹣3<x<5},
∴∁UA═{x|x≤a},
要使B∩(∁RA)≠∅,
则a>﹣3.
故选B.
【点评】本题主要考查集合关系的应用,比较基础.
设偶函数f(x)=loga|x﹣b|在(﹣∞,0)上是增函数,则有( )
A.f(a+1)≥f(b+2) B.f(a+1)<f(b+2) C.f(a+1)≤f(b+2) D.f(a+1)>f(b+2)
知识点:10.对数函数及其性质
D
【考点】奇偶性与单调性的综合;对数函数的单调性与特殊点.
【分析】由已知中偶函数f(x)=loga|x﹣b|在(﹣∞,0)上是增函数,根据偶函数的定义及复合函数单调性“同增异减”的原则,我们可以求出b值及a的范围,进而根据函数的单调性,得到答案.
【解答】解:∵函数f(x)=loga|x﹣b|为偶函数
∴f(﹣x)=f(x)
即loga|﹣x﹣b|=loga|x﹣b|
则|﹣x﹣b|=|x﹣b|
故b=0
则f(x)=loga|x|
u=|x|在区间(﹣∞,0)上为减函数,在区间(0,+∞)上为增函数,
而函数f(x)在(﹣∞,0)上是增函数,
根据复合函数“同增异减”的原则,则函数y=logau为减函数
则0<a<1
则函数f(x)=loga|x﹣b|在0,+∞)上是减函数,
则1<a+1<2=b+2
故f(a+1)>f(b+2)
故选D
【点评】本题考查的知识点是奇偶性与单调性的综合,对数函数的单调性与特殊点,其中根据偶函数及复合函数单调性“同增异减”的原则,求出b值及a的范围,及函数的单调性,是解答本题的关键.
已知集合A={﹣1,0,1},B={x|﹣1≤x<1},则A∩B=( )
A.{0} B.{﹣1,0} C.{0,1} D.{﹣1,0,1}
知识点:3.集合的基本运算
B
【考点】交集及其运算.
【专题】集合.
【分析】找出A与B的公共元素,即可确定出两集合的交集.
【解答】解:∵A={﹣1,0,1},B={x|﹣1≤x<1},
∴A∩B={﹣1,0}.
故选B
【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
如果指数函数y=(a﹣1)x是增函数,则a的取值范围是( )
A.a>2 B.a<2 C. a>1 D.1<a<2
知识点:8.指数函数及其性质
A
【考点】指数函数的图像与性质.
【专题】函数的性质及应用.
【分析】由指数函数的单调性可得a﹣1>1,解不等式可得.
【解答】解:∵指数函数y=(a﹣1)x是增函数,
∴a﹣1>1,解得a>2
故选:A
【点评】本题考查指数函数的单调性,属基础题.
设全集U={x∈N+|x<6},集合A={1,3},B={3,5},则∁U(A∪B)=( )
A.{1,4} B.{1,5} C.{2,4} D.{2,5}
知识点:3.集合的基本运算
C
【考点】交、并、补集的混合运算.
【专题】计算题.
【分析】由全集U={x∈N+|x<6},可得U={1,2,3,4,5},然后根据集合混合运算的法则即可求解.
【解答】解:∵A={1,3},B={3,5},
∴A∪B={1,3,5},
∵U={x∈N+|x<6}={1,2,3,4,5},
∴∁U(A∪B)={2,4},
故选C.
【点评】本题考查了集合的基本运算,属于基础知识,注意细心运算.
已知奇函数f(x)在[﹣1,0]上为单调减函数,又α,β为锐角三角形内角,则( )
A. f(cosα)>f(cosβ) B.f(sinα)>f(sinβ) C.f(sinα)<f(cosβ) D.f(sinα)>f(cosβ)
知识点:5.奇偶性与周期性
C
【考点】余弦函数的单调性.
【专题】计算题;压轴题.
【分析】由“奇函数y=f(x)在[﹣1,0]上为单调递减函数”可知f(x)在[0,1]上为单调递减函数,再由“α、β为锐角三角形的两内角”可得到α+β>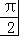 ,转化为α>
,转化为α>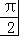 ﹣β,两边再取正弦,可得sinα>sin(
﹣β,两边再取正弦,可得sinα>sin(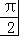 ﹣β)=cosβ>0,由函数的单调性可得结论.
﹣β)=cosβ>0,由函数的单调性可得结论.
【解答】解:∵奇函数y=f(x)在[﹣1,0]上为单调递减函数,
∴f(x)在[0,1]上为单调递减函数,
∴f(x)在[﹣1,1]上为单调递减函数,
又α、β为锐角三角形的两内角,
∴α+β>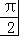 ,
,
∴α>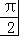 ﹣β,
﹣β,
∴sinα>sin(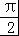 ﹣β)=cosβ>0,
﹣β)=cosβ>0,
∴f(sinα)<f(cosβ).
故选C.
【点评】题主要考查奇偶性和单调性的综合运用,还考查了三角函数的单调性.属中档题.
定义集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )
A.0 B.6 C.12 D.18
知识点:3.集合的基本运算
D
【考点】进行简单的合情推理.
【分析】根据定义的集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},将集合A={0,1},B={2,3}的元素代入求出集合A⊙B后,易得答案.
【解答】解:当x=0时,z=0,
当x=1,y=2时,z=6,
当x=1,y=3时,z=12,
故所有元素之和为18,
故选D
【点评】这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.
函数f(x)=log2 的图象( )
的图象( )
A.关于原点对称 B.关于直线y=﹣x对称
C.关于y轴对称 D.关于直线y=x对称
知识点:10.对数函数及其性质
A
【考点】对数函数的图像与性质.
【专题】函数的性质及应用.
【分析】先根据函数的奇偶性的定义判断函数f(x)为奇函数,再根据奇函数的性质可得函数f(x)的图象关于原点对称.
【解答】解:∵函数f(x)=log2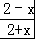 ,∴
,∴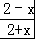 >0,求得﹣2<x<2,可得函数的定义域为(﹣2,2),关于原点对称.
>0,求得﹣2<x<2,可得函数的定义域为(﹣2,2),关于原点对称.
再根据 f(﹣x)=log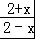 =﹣f(x),可得函数f(x)为奇函数,故函数的图象关于原点对称,
=﹣f(x),可得函数f(x)为奇函数,故函数的图象关于原点对称,
故选:A.
【点评】本题主要考查求函数的定义域,函数的奇偶性的判断,奇函数的图象特征,属于基础题.
已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x,则在R上f(x)的表达式是( )
A.﹣x(x﹣2) B.x(|x|﹣2) C.|x|(x﹣2) D.|x|(|x|﹣2)
知识点:5.奇偶性与周期性
B
【考点】函数奇偶性的性质;函数的表示方法.
【分析】设x<0,则﹣x>0,利用当x≥0时f(x)的解析式,求出f(﹣x)的解析式,再利用奇函数的定义,求出x<0时的解析式,综合在一起,可得在R上f(x)的表达式.
【解答】解:设x<0,则﹣x>0,
∵当x≥0时,f(x)=x2﹣2x,
∴f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x,
又∵y=f(x)是定义在R上的奇函数,f(﹣x)=﹣f(x),
∴﹣f(x)=x2+2x,
∴f(x)=﹣x2﹣2x,
故则在R上f(x)的表达式是 x(|x|﹣2),
故选B.
【点评】本题考查利用奇函数的定义求函数的解析式的方法.
函数y= 的值域是( )
的值域是( )
A.[﹣1,1] B.(﹣1,1] C.[﹣1,1) D.(﹣1,1)
知识点:2.定义域与值域
B
【考点】函数的值域.
【分析】进行变量分离y=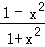 =
=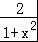 ﹣1,若令t=1+x2则可变形为y=
﹣1,若令t=1+x2则可变形为y=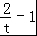 (t≥1)利用反比例函数图象求出函数的值域.
(t≥1)利用反比例函数图象求出函数的值域.
【解答】解法一:y=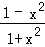 =
=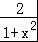 ﹣1.∵1+x2≥1,
﹣1.∵1+x2≥1,
∴0<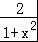 ≤2.∴﹣1<y≤1.
≤2.∴﹣1<y≤1.
解法二:由y=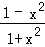 ,得x2=
,得x2=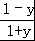 .
.
∵x2≥0,∴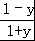 ≥0,解得﹣1<y≤1.
≥0,解得﹣1<y≤1.
故选B
【点评】此类分式函数的值域通常采用逆求法、分离变量法,应注意理解并加以运用.
解法三:令x=tanθ(﹣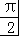 <θ<
<θ<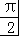 ),则y=
),则y=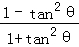 =cos2θ.
=cos2θ.
∵﹣π<2θ<π,
∴﹣1<cos2θ≤1,即﹣1<y≤1.
函数 的图象大致是( )
的图象大致是( )
A. B.
B. C.
C. D.
D.
知识点:15.函数的图像
A
【考点】余弦函数的图象.
【专题】数形结合.
【分析】由函数的解析式可以看出,函数的零点呈周期性出现,且法自变量趋向于正无穷大时,函数值在x轴上下震荡,幅度越来越小,而当自变量趋向于负无穷大时,函数值在x轴上下震荡,幅度越来越大,由此特征对四个选项进行判断,即可得出正确选项.
【解答】解:∵函数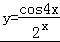
∴函数的零点呈周期性出现,且法自变量趋向于正无穷大时,函数值在x轴上下震荡,幅度越来越小,而当自变量趋向于负无穷大时,函数值在x轴上下震荡,幅度越来越大,
A选项符合题意;
B选项振幅变化规律与函数的性质相悖,不正确;
C选项是一个偶函数的图象,而已知的函数不是一个偶函数故不正确;
D选项最高点离开原点的距离的变化趋势不符合题意,故不对.
综上,A选项符合题意
故选A
【点评】本题考查余弦函数的图象,解题的关键是根据余弦函数的周期性得出其零点周期性出现,再就是根据分母随着自变量的变化推测出函数图象震荡幅度的变化,由这些规律对照四个选项选出正确答案.
已知集合A={﹣1,1},B={x|1≤2x<4},则A∩B等于( )
A.{﹣1,0,1} B.{1} C.{﹣1,1} D.{0,1}
知识点:3.集合的基本运算
B
【考点】交集及其运算.
【专题】计算题.
【分析】利用指数函数的性质求出集合B中不等式的解集,确定出集合B,找出A与B的公共元素,即可求出两集合的交集.
【解答】解:由集合B中的不等式变形得:20≤2x<22,
解得:0≤x<2,
∴B=[0,2),又A={﹣1,1},
则A∩B={1}.
故选:B
【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
已知函数f(x)= ,则f﹣1(1)= .
,则f﹣1(1)= .
知识点:5.行列式
1
【考点】反函数;二阶矩阵.
【专题】常规题型;计算题.
【分析】本题由矩阵得到f(x)的表达式,再由反函数的知识算出.
【解答】解:由f(x)= =2x﹣1,由反函数的性质知2x﹣1=1,解得x=1所以f﹣1(1)=1.
=2x﹣1,由反函数的性质知2x﹣1=1,解得x=1所以f﹣1(1)=1.
故答案为:1.
【点评】原函数的图象与反函数的图象关于y=x对称,亦即b=f(a)与a=f﹣1(b)是等价的.
函数f(x)=log3(2x﹣1)的定义域为 .
知识点:2.定义域与值域
{x|x>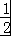 }
}
【考点】函数的定义域及其求法.
【专题】函数的性质及应用.
【分析】根据对数函数的真数大于0,求出函数的定义域即可.
【解答】解:∵2x﹣1>0,
∴x>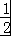 ,
,
∴函数的定义域是:{x|x>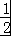 },
},
故答案为::{x|x>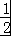 }.
}.
【点评】本题考察了函数的定义域问题,考察对数函数的性质,是一道基础题.
设f(x)= ,则f(f(5))= .
,则f(f(5))= .
知识点:12.绝对值函数与分段函数及其他函数
1
【考点】函数的值.
【专题】计算题.
【分析】根据函数解析式应先代入下面的式子求出f(5)的值,再代入对应的解析式求出f(f(5))的值.
【解答】解:由题意知,f(x)=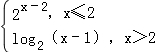 ,
,
则f(5)=log24=2,
∴f(f(5))=f(2)=22﹣2=1.
故答案为:1.
【点评】本题是分段函数求值问题,对应多层求值按“由里到外”的顺序逐层求值,一定要注意自变量的值所在的范围,然后代入相应的解析式求解.
函数f(x)= +
+ 的定义域是 .
的定义域是 .
知识点:2.定义域与值域
{2}
【考点】函数的定义域及其求法.
【专题】函数的性质及应用.
【分析】直接利用开偶次方,被开方数非负,化简求解即可.
【解答】解:要使函数有意义,
则 ,解得:x=2.
,解得:x=2.
函数的定义域为:{2}.
故答案为:{2}.
【点评】本题考查函数的定义域的求法,基本知识的考查.
已知指数函数 ,当x∈(0,+∞)时,有y>1,解关于x的不等式loga(x﹣1)≤loga(x2+x﹣6).
,当x∈(0,+∞)时,有y>1,解关于x的不等式loga(x﹣1)≤loga(x2+x﹣6).
知识点:8.指数函数及其性质
【考点】指数函数的单调性与特殊点;对数函数的单调性与特殊点.
【专题】计算题.
【分析】由已知中指数函数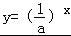 ,当x∈(0,+∞)时,有y>1,我们易判断出底数
,当x∈(0,+∞)时,有y>1,我们易判断出底数 的取值范围,进而判断出a的取值范围,然后根据函数的单调性,将不等式转化为一个二次不等式,即可得到答案.
的取值范围,进而判断出a的取值范围,然后根据函数的单调性,将不等式转化为一个二次不等式,即可得到答案.
【解答】解:∵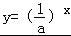 在x∈(0,+∞)时,有y>1,∴
在x∈(0,+∞)时,有y>1,∴ ,
,
于是由loga(x﹣1)≤loga(x2+x﹣6),得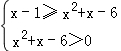 ,
,
解得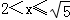 ,
,
∴不等式的解集为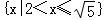 .
.
【点评】本题考查的知识点是指数函数的单调性及对数函数的单调性,其中根据已知条件,判断出a的取值范围,是解答本题的关键.
设函数
(1)求函数的定义域;
(2)求函数的值域;
(3)求函数的单调区间.
知识点:2.定义域与值域
【考点】指数函数综合题.
【专题】函数的性质及应用.
【分析】(1)由4+3x﹣x2=﹣(x+1)(x﹣4)≥0 可求得x的范围,即为函数的定义域.
(2)令t=4+3x﹣x2,由﹣1≤x≤4,求得t的范围,可得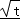 的范围,从而求得
的范围,从而求得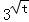 的范围,即为函数的值域.
的范围,即为函数的值域.
(3)由于二次函数t=4+3x﹣x2 的对称轴为x=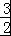 ,且﹣1≤x≤4,由此可得函数的增区间、减区间.
,且﹣1≤x≤4,由此可得函数的增区间、减区间.
【解答】解:(1)由4+3x﹣x2=﹣(x+1)(x﹣4)≥0 可得﹣1≤x≤4,故函数的定义域为[﹣1,4].
(2)令t=4+3x﹣x2,由﹣1≤x≤4,可得 0≤t≤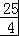 ,0≤
,0≤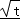 ≤
≤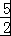 ,1≤
,1≤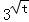 ≤
≤ ,而
,而  =9
=9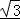 ,∴1≤
,∴1≤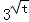 ≤9
≤9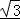 ,
,
∴1≤f(x)≤9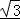 ,故函数的值域为
,故函数的值域为 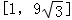 .
.
(3)由于二次函数t=4+3x﹣x2 的对称轴为x=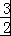 ,且﹣1≤x≤4,故函数的增区间为[﹣1,
,且﹣1≤x≤4,故函数的增区间为[﹣1,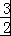 ],减区间为[
],减区间为[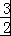 ,4].
,4].
【点评】本题主要考查指数型复合函数的定义域、值域以及单调性,体现了转化的数学思想,属于中档题.
已知A={x| <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(Ⅰ)求A∩B和A∪B;
(Ⅱ)定义A﹣B={x|x∈A且x∉B},求A﹣B和B﹣A.
知识点:3.集合的基本运算
【考点】交集及其运算.
【专题】集合.
【分析】(Ⅰ)求出A与B中其他不等式的解集确定出A与B,找出两集合的交集,并集即可;
(Ⅱ)根据A﹣B的定义,求出A﹣B与B﹣A即可.
【解答】解:(Ⅰ)由A中的不等式变形得:3﹣1<3x<32,
解得:﹣1<x<2,即A=(﹣1,2),
由B中的不等式变形得:log2x>0=log21,得到x>1,
∴B=(1,+∞),
则A∩B=(1,2);A∪B=(﹣1,+∞);
(Ⅱ)∵A=(﹣1,2),B=(1,+∞),A﹣B={x|x∈A且x∉B},
∴A﹣B=(﹣1,1];B﹣A=[2,+∞).
【点评】此题考查了交集及其运算,并集及其运算,以及新定义,熟练掌握各自的定义是解本题的关键.
已知定义在(0,+∞)上的函数f(x)对任意正数p,q都有 ,当x>4时,f(x)>
,当x>4时,f(x)> ,且f(
,且f( )=0.
)=0.
(1)求f(2)的值;
(2)证明:函数f(x)在(0,+∞)上是增函数;
(3)解关于x的不等式f(x)+f(x+3)>2.
知识点:3.单调性与最大(小)值
【考点】函数与方程的综合运用.
【专题】转化思想;数学模型法;函数的性质及应用.
【分析】(1)抽象函数常用赋值法求解;
(2)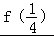 =
=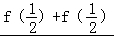 ﹣
﹣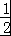 =﹣
=﹣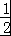 .按照单调性的定义,任取0<x1<x2,则f(x2)﹣f(x1)=
.按照单调性的定义,任取0<x1<x2,则f(x2)﹣f(x1)= ﹣
﹣ =
=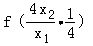 ﹣
﹣ =
=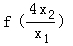 +
+ ﹣1=
﹣1=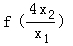 ﹣
﹣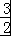 ,
,
由于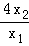 >4,可得
>4,可得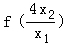 ﹣
﹣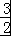 >0,即可证明.
>0,即可证明.
(3)解抽象函数的不等式,常化为f(m)>f(n)的形式,然后结合单调性求解.
【解答】(1)解: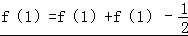 ,∴
,∴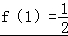 ,
,
∴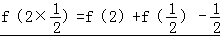 ,
,
解得f(2)=1.
(2)证明: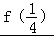 =
=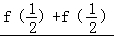 ﹣
﹣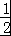 =﹣
=﹣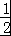 .
.
任取0<x1<x2,
则f(x2)﹣f(x1)=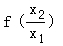 ﹣
﹣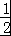 =
=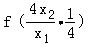 ﹣
﹣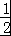 =
=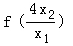 +
+ ﹣1=
﹣1=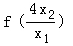 ﹣
﹣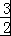 ,
,
∵ >4,∴
>4,∴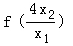 ﹣
﹣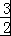 >0,
>0,
∴f(x2)﹣f(x1)>0,即f(x2)>f(x1).
∴函数f(x)在(0,+∞)上是增函数.
(3)解:∵f(2×2)=f(2)+f(2)﹣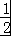 =1+1﹣
=1+1﹣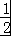 =
=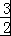 .
.
f(x)+f(x+3)=f(x2+3x)+ >2.
>2.
∴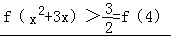 ,
,
∴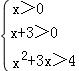 ,解得x∈(1,+∞),
,解得x∈(1,+∞),
∴原不等式的解集为(1,+∞).
【点评】本题考查了抽象函数的求值与单调性、不等式的性质,考查了变形推理能力与计算能力,属于中档题.
计算:
(1)(2 )
) ﹣(﹣7.8)0﹣(3
﹣(﹣7.8)0﹣(3 )
) +(
+( )﹣2
)﹣2
(2)( )
) •
• .
.
知识点:7.指数与指数幂的运算
【考点】有理数指数幂的化简求值.
【专题】函数的性质及应用.
【分析】(1)(2)利用指数幂的运算性质即可得出.
【解答】解:(1)原式=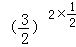 ﹣1﹣
﹣1﹣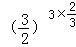 +
+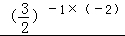 =
= ﹣1﹣
﹣1﹣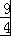 +
+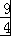 =
= .
.
(2)原式=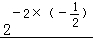 •
•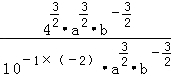 =
=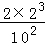 =
=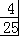 .
.
【点评】本题考查了指数幂的运算性质,考查了推理能力与计算能力,属于中档题.
已知f(x)=16x﹣2×4x+5,x∈[﹣1,2].
(1)设t=4x,x∈[﹣1,2],求t的最大值与最小值;
(2)求f(x)的最大值与最小值.
知识点:6.二次函数
【考点】函数的最值及其几何意义.
【专题】函数的性质及应用.
【分析】(1)由指数函数的单调性,即可求得t的最值;
(2)令t=4x,(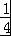 ≤t≤16)原式变为:y=t2﹣2t+5=(t﹣1)2+4,求出对称轴t=1,讨论和区间的关系,即可得到所求最值.
≤t≤16)原式变为:y=t2﹣2t+5=(t﹣1)2+4,求出对称轴t=1,讨论和区间的关系,即可得到所求最值.
【解答】解:(1)由t=4x在[﹣1,2]是单调增函数,
即有x=2时,t取得最大值为16,x=﹣1时,t取得最小值为 ;
;
(2)令t=4x,( ≤t≤16)原式变为:
≤t≤16)原式变为:
y=t2﹣2t+5=(t﹣1)2+4,
当t=1时,此时x=1,f(x)取得最小值4;
当t=16时,此时x=2,f(x)取得最大值229.
【点评】本题考查可化为二次函数的最值的求法,注意运用换元法和指数函数的单调性,考查运算能力,属于中档题.