已知i为虚数单位,若复数(1+ai)(2+i)是纯虚数,则实数a等于( )
A.2 B. C.
C. D.﹣2
D.﹣2
知识点:3.复数代数形式的四则运算
A
【考点】复数的代数表示法及其几何意义.
【专题】计算题.
【分析】利用复数的运算法则进行化简,然后再利用纯虚数的定义即可得出.
【解答】解:∵复数(1 +ai)(2+i)=2﹣a+(1+2a)i是纯虚数,∴
+ai)(2+i)=2﹣a+(1+2a)i是纯虚数,∴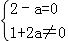 ,解得a=2.
,解得a=2.
故选A.
【点评】熟练掌握复数的运算法则、纯虚数的定义是解题的关键.
抛物线y2=4x上点P(a,2)到焦点F的距离为( )
A.1 B.2 C.4 D.8
知识点:3.抛物线
B
【考点】抛物线的简单性质.
【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】根据抛物线的定义可知点P到准线的距离与点P到焦点的距离相等,故点P到抛物线焦点的距离为点p的横坐标+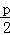 ,求出P的横坐标进而求解.
,求出P的横坐标进而求解.
【解答】解:∵抛物线y2=4x=2px,
∴p=2,
P(a,2)代入y2=4x,可得xp=1
由抛物线的定义知的,点P到抛物线焦点的距离为xp+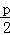 =1+1=2,
=1+1=2,
故选:B.
【点评】本题主要考查了抛物线的定义,充分利用了抛物线上的点到准线的距离与点到焦点的距离相等这一特性.
设f(x)=3x2ex,则f′(2)=( )
A.12e B.12e2 C.24e D.24e2
知识点:2.导数的计算
D
【考点】导数的运算.
【专题】计算题;函数思想;定义法;导数的概念及应用.
【分析】求函数的导数即可得到结论.
【解答】解:f′(x)=6xex+3x2ex,
∴f′(2)=12e2+12e2=24e2.
故选:D.
【点评】本题主要考查导数的计算,要求熟练掌握常见函数的导数公式,比较基础.
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.3 B.2 C.1 D.
知识点:1.变化率与导数
A
【考点】导数的几何意义.
【分析】根据斜率,对已知函数求导,解出横坐标,要注意自变量的取值区间.
【解答】解:设切点的横坐标为(x0,y0)
∵曲线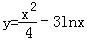 的一条切线的斜率为
的一条切线的斜率为 ,
,
∴y′=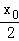 ﹣
﹣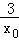 =
= ,解得x0=3或
,解得x0=3或 x0=﹣2(舍去,不符合题意
x0=﹣2(舍去,不符合题意 ),即
),即 切点的横坐标为3
切点的横坐标为3
故选A.
【点评】考查导数的几何意义,属于基础题,对于一个给定的函数来说,要考虑它的定义域.比如,该题的定义域为{x>0}.
如图是函数y=f(x)的导函数y=f′(x)的图象,则下列判断正确的是( )

A.在区间(﹣3,1)上y=f(x)是增函数 B.在区间(1,3)上y=f(x)是减函数
C.在区间(4,5)上y=f(x)是增函数 D.在x=2时y=f(x)取到极小值
知识点:3.导数在研究函数中的应用
C
【考点】利用导数研究函数的单调性.
【专题】计算题;数形结合;导数的综合应用.
【分析】由图象可判断导数的正负,从而确定函数的增减性及极值,从而确定答案即可.
【解答】解:由图象可知,
当﹣3≤x<﹣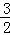 时,f′(x)<0;
时,f′(x)<0;
当﹣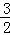 <x<2时,f′(x)>0;
<x<2时,f′(x)>0;
当2<x<4时,f′(x)<0;
当4 <x<5时,f′(x)>0;
<x<5时,f′(x)>0;
故函数y=f(x)在(﹣3,﹣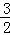 ),(2,4)上是减函数,
),(2,4)上是减函数,
在(﹣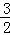 ,2),(4,5)上是增函数;
,2),(4,5)上是增函数;
在x=2时取得极大值;
故选:C.
【点评】本题考查了导数的综合应用及数形结合的思想应用,属于中档题.
设函数f(x)=xm+ax的导函数f′(x)=2x+1,则数列{ }(n∈N*)的前n项和是( )
}(n∈N*)的前n项和是( )
A. B.
B. C.
C. D.
D.
知识点:2.导数的计算
A
【考点】数列的求和;导数的运算.
【专题】计算题.
【分析】函数f(x)=xm+ax的导函数f′(x)=2x+1,先求原函数的导数,两个导数进行比较即可求出m,a,然后利用裂项法求出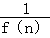 的前n项和,即可.
的前n项和,即可.
【解答】解:f′(x)=mxm﹣1+a=2x+1,
∴a=1,m=2,∴f(x)=x(x+1 ),
),
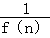 =
= =
=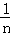 ﹣
﹣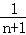 ,
,
用裂项法求和得Sn=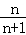 .
.
故选A
【点评】本题考查数列的求和运算,导数的运算法则,数列求和时注意裂项法的应用,是好题,常考题,基础题.
下列有关命题的说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
B.“x=1”是“x2﹣5x﹣6=0”的必要不充分条件.
C.命题“∃x∈R使得x2+x+1<0”的否定是:“∀x∈R,均有x2+x+1<0”
D.命题“若x=y,则sinx=siny”的逆否命题为真命题
知识点:5.充分条件与必要条件
D
【考点】命题的真假判断与应用.
【专题】综合题;对应思想;简易逻辑.
【分析】写出命题的否定判断A;求解方程后结合充分必要条件的判断方法判断B;写出特称命题的否定判断C;由互为逆否命题的两个命题共真假判断D.
【解答】解:命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”,故A错误;
由x2﹣5x﹣6=0,解得x=﹣1或x=6,
∴“x=1”是“x2﹣5x﹣6=0”的既不充分也不必要条件,故B错误;
命题“∃x∈R使得x2+x+1<0”的否定是:“∀x∈R,均有x2+x+1≥0”,故C错误;
命题“若x=y,则sinx=siny”为真命题,∴其逆否命题为真命题 ,故D正确.
,故D正确.
故选:D.
【点评】本题考查命题的真假判断与应用,考查了命题的否定和否命题,训练了充分必要条件的判断方法,是基础题.
已知{an}为等差数列,其公差为﹣2,且a7是a3与a9的等比中项,Sn为{an}的前n项和,n∈N*,则S10的值为( )
A.﹣110 B.﹣90 C.90 D.110
知识点:3.等差数列的前n项和
D
【考点】等差数列的前n项和;等比数列的性质.
【专题】等差数列与等比数列.
【分析】通过a7是a3与a9的等比中项,公差为﹣2,求出
【解答】解:a7是a3与a9的等比中项,公差为﹣2,所以a72=a3•a9,
∵{an}公差为﹣2,
∴a3=a7﹣4d=a7+8,a9=a7+2d=a7﹣4,
所以a72=(a7+8)(a7﹣4),所以a7=8,所以a1=20,
所以S10=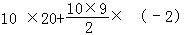 =110
=110
故选D
【点评】本题是基础题,考查等差数列的前n项和,等比数列的应用,考查计算能力,常考题型.
已知x>0,y>0,且2x+y=1,则xy的最大值是( )
A. B.
B. C.4 D.8
C.4 D.8
知识点:4.基本不等式
B
【考点】基本不等式.
【专题】不等式的解法及应用.
【分析】利用基本不等式的性质即可得出.
【解答】解:∵x>0,y>0,且2x+y=1,
∴xy=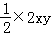
 =
= ,当且仅当2x=y>0,2x+y=1,即
,当且仅当2x=y>0,2x+y=1,即 ,y=
,y= 时,取等号,此时,xy的最大值是
时,取等号,此时,xy的最大值是 .
.
故选B.
【点评】熟练掌握基本不等式的性质是解题的关键.
如果x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
A.(0,1) B.(0,2) C.(1,+∞) D.(0,+∞)
知识点:1.椭圆
A
【考点】椭圆的标准方程.
【专题】圆锥曲线的定义、性质与方程.
【分析】利用椭圆的定义求解.
【解答】解:∵x2+ky2=2表示焦点在y轴上的椭圆,
把x2+ky2=2转化为椭圆的标准方程,得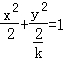 ,
,
∴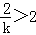 ,解得0<k<1.
,解得0<k<1.
∴实数k的取值范围是(0,1).
故选:A.
【点评】本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意椭圆性质的灵活运用.
设等差数列{an}的前n项和为Sn,若a1=﹣11,a4+a6=﹣6,则当Sn取最小值时,n等于( )
A.6 B.7 C.8 D.9
知识点:3.等差数列的前n项和
A
【考点】等差数列的前n项和.
【专题】等差数列与等比数列.
【分析】条件已提供了首项,故用“a1,d”法,再转化为关于n的二次函数解得.
【解答】解:设该数列的公差为d,则a4+a6=2a1+8d=2×(﹣11)+8d=﹣6,解得d=2,
所以
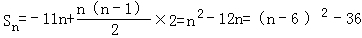 ,所以当n=6时,Sn取最小值.
,所以当n=6时,Sn取最小值.
故选A.
【点评】本题考查等差数列的通项公式以及前n项和公式的应用,考查二次函数最值的求法及计算能力.
设F1,F2分别是双曲线 的左、右焦点.若双曲线上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,则双曲线离心率为( )
的左、右焦点.若双曲线上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,则双曲线离心率为( )
A. B.
B. C.
C. D.
D.
知识点:2.双曲线
B
【考点】双曲线的简单性质.
【专题】压轴题.
【分析】由题设条件设|AF2|=1,|AF1|=3,双曲线中2a=|AF1|﹣|AF2|=2, ,由此可以求出双曲线的离心率.
,由此可以求出双曲线的离心率.
【解答】解:设F1,F2分别是双曲线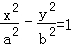 的左、右焦点.
的左、右焦点.
若双曲线上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,
设|AF2|=t,|AF1|=3t,(t>0)
双曲线中2a=|AF1|﹣|AF2|=2t,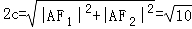 t,
t,
∴离心率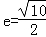 ,
,
故选B.
【点评】挖掘题设条件,合理运用双曲线的性质能够准确求解.
若等比数列{an}满足 ,则
,则 = .
= .
知识点:4.等比数列及其性质
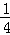
【考点】等比数列的通项公式.
【专题】方程思想;转化思想;等差数列与等比数列.
【分析】由等比数列{an}的性质可得: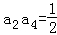 =a1a5=
=a1a5=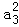 ,即可得出.
,即可得出.
【解答】解:由等比数列{an}的性质可得: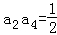 =a1a5=
=a1a5=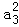 ,
,
则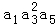 =
=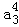 =
=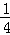 .
.
故答案为: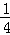 .
.
【点评】本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.
若实数x,y满足 则z=x+2y的最大值是 .
则z=x+2y的最大值是 .
知识点:3.二元一次不等式(组)与简单的线性规划
2
【考点】简单线性规划.
【专题】数形结合.
【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=x+2y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.
【解答】解:满足题中约束条件的可行域如图所示.
目标函数z=x+2y取得最大值,
即使得函数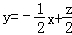 在y轴上的截距最大.
在y轴上的截距最大.
结合可行域范围知,当其过点P(0,1)时,Zmax=0+2×1=2.
故答案为:2.

【点评】本题考查简单线性规划,解题的重点是作出正确的约束条件对应的区域,根据目标函数的形式及图象作出正确判断找出最优解,
圆(x﹣a)2+y2=1与双曲线x2﹣y2=1的渐近线相切,则a的值是 (只写一个答案给3分) .
知识点:4.直线与圆的位置关系
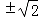
【考点】直线与圆的位置关系.
【专题】计算题;直线与圆.
【分析】根据圆方程,得到圆心坐标C(a,0),圆与双曲线的渐近线相切,说明C到渐近线的距离等于半径1,列出方程求出a的值即可.
【解答】解:圆(x﹣a)2+y2=1∴圆心坐标C(a,0),圆的半径为:1.
∵双曲线x2﹣y2=1的渐近线为x±y=0,
双曲线x2﹣y2=1的渐近线与圆(x﹣a)2+y2=1相切,
∴C到渐近线的距离为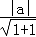 =1,解得a=
=1,解得a=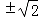
故答案为: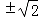 .
.
【点评】本题给出双曲线的渐近线与已知圆相切,点到直线的距离公式,着重考查了直线与圆的位置关系和双曲线的简单性质等知识.
椭圆 的焦点为F1,F2,点P在椭圆上,若|PF1|=4,∠F1PF2的大小为 .
的焦点为F1,F2,点P在椭圆上,若|PF1|=4,∠F1PF2的大小为 .
知识点:1.椭圆
120°
【考点】椭圆的简单性质.
【专题】计算题;圆锥曲线的定义、性质与方程.
【分析】由|PF1|+|PF2|=6,且|PF1|=4,易得|PF2|,再利用余弦定理,即可求得结论.
【解答】解:∵|PF1|+|PF2|=2a=6,|PF1|=4,
∴|PF2|=6﹣|PF1|=2.
在△F1PF2中,cos∠F1PF2=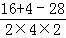 =﹣
=﹣ ,
,
∴∠F1PF2=120°.
故答案为:120°
【点评】本题主要考查椭圆定义的应用及焦点三角形问题,考查余弦定理的运用,考查学生的计算能力,属于基础题.
已知{an}是首项为19,公差为﹣2的等差数列,Sn为{an}的前n项和.
(1)求通项an及Sn;
(2)设{bn﹣an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及其前n项和Tn.
知识点:3.等差数列的前n项和
【考点】等差数列的前n项和;数列的求和.
【专题】计算题.
【分析】(1)直接代入等差数列的 通项公式及前n项和公式可求an及Sn
通项公式及前n项和公式可求an及Sn
(2))利用等比数列的通项公式可求bn﹣an,结合(1)中的an代入可求bn,利用分组求和及等比数列的前n项和公式可求
【解答】解:(1)因为an是首项为a1=19,公差d=﹣2的等差数列,
所以an=19﹣2(n﹣1)=﹣2n+21,
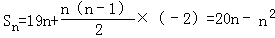 .
.
(2)由题意bn﹣an=3n﹣1,所以bn=an+3n﹣1,
Tn=Sn+(1+3+32+…+3n﹣1)
=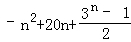 .
.
【点评】本题主要考查了等差数列的通项公式及前n项和公式,等比数列的通项公式,分组求和及等比数列的求和公式等知识的简单运用.
设函数f(x)=x3﹣3ax2+3bx的图象与直线12x+y﹣1=0相切于点(1,﹣11).
(Ⅰ)求a,b的值;
(Ⅱ)讨论函数f(x)的单调性.
知识点:3.导数在研究函数中的应用
【考点】导数的几何意义;函数单调性的判断与 证明.
证明.
【分析】(Ⅰ)函数在切点处的导数值为切线斜率,切点在切线上,列方程解.
(Ⅱ)导函数大于0对应区间是单调递增区间;导函数小于0对应区间是单调递减区间.
【解答】解:(Ⅰ)求导得f′(x)=3x2﹣6ax+3b.
由于f(x)的图象与直线12x+y﹣1=0相切于点(1,﹣11),
所以f(1)=﹣11,f′(1)=﹣12,即:
1﹣3a+3b=﹣11,3﹣6a+3b=﹣12
解得:a=1,b=﹣3.
(Ⅱ)由a=1,b=﹣3得:f′(x)=3x2﹣6ax+3b=3(x2﹣2x﹣3)=3(x+1)(x﹣3)
令f′(x)>0,解得x<﹣1或x>3;
又令f′(x)<0,解得﹣1<x<3.
故当x∈(﹣∞,﹣1)时,f(x)是增函数,
当x∈(3,+∞)时,f(x)也是增函数,
但当x∈(﹣1,3)时,f(x)是减函数.
【点评】考查导数的几何意义及利用导数求函数的单调区间.
在△ABC中, ,
, .
.
(Ⅰ)求sinC的值;
(Ⅱ)设BC=5,求△ABC的面积.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】两角和与差的正弦函数;同角三角函数间的基本关系.
【专题】计算题.
【分析】(Ⅰ)先利用同角三角函数的基本关系求得sinA和sinB的值,进而根据sinC=sin(A+B)利用正弦的两角和公式求得答案.
(Ⅱ)先利用正弦定理求得AC,进而利用三角形面积公式求得三角形的面积.
【解答】解:(Ⅰ)由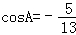 ,得
,得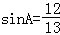 ,
,
由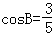 ,得
,得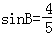 .
.
所以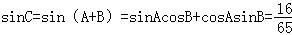 .
.
(Ⅱ)由正弦定理得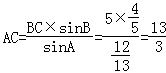 .
.
所以△ABC的面积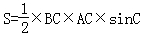 =
=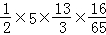 =
=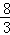 .
.
【点评】本题主要考查了同角三角函数的基本关系的应用和正弦的两角和公式的应用.考查了学生对三角函数基础知识的理解和灵活运用.
某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件.由于市场饱和顾客要求提高,公司计划投入资金进行产品升级.据市场调查,若投入x万元,每件产品的成本将降低 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为f(x)(单位:万元 ).
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为f(x)(单位:万元 ).
(1)求f(x)的函数解析式;
(2)求f(x)的最大值,以及f(x)取得最大值时x的值.
知识点:14.函数的应用问题
【考点】函数模型的选择与应用.
【专题】应用题;函数的性质及应用.
【分析】(1)求出产品升级后每件的成本、利润及年销售量,则利润的函数表达式可求;
(2)利用基本不等式求出f(x)的最大值.
【解答】解:(1)依题意,产品升级后,每件的成本为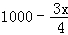 元,利润为
元,利润为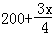 元,
元,
年销售量为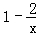 万件,
万件,
纯利润为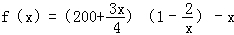 ,
,
=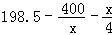 (万元);
(万元);
(2) ,
,
=178.5.
等号当且仅当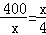 ,
,
即x=40(万元).
即最大值时的x的值为40
【点评】本题考查了函数模型的选择及应用,训练了简单的建模思想方法,考查了利用基本不等式求最值,是中档题.
已知函数
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的极值;利用导数研究函数的单调性.
【专题】函数的性质及应用.
【分析】(1)因为当函数的导数为0时,函数有极值,所以当a=0时,必须先在定义域中求函数f(x)的导数,让导数等于0,求x的值,得到极值点,在列表判断极值点两侧导数的正负,根据所列表,判断何时有极值.
(2)因为当函数为增函数时,导数大于0,若f(x)在区间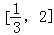 上是增函数,则f(x)在区间
上是增函数,则f(x)在区间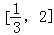 上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间
上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间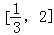 上恒大于0即可.
上恒大于0即可.
【解答】解:(1)函数的定义域为(0,+∞)
∵ 当a=0时,f(x)=2x﹣lnx,则
当a=0时,f(x)=2x﹣lnx,则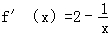
∴x,f'(x),f(x)的变化情况如下表
x | (0, |
| ( |
f'(x) | ﹣ | 0 | + |
f(x) |
| 极小值 |
|
∴当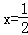 时,f(x)的极小值为1+ln2,函数无极大值.
时,f(x)的极小值为1+ln2,函数无极大值.
(2)由已知,得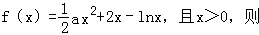

若a=0,由f'(x)>0得 ,显然不合题意
,显然不合题意
若a≠0∵函数f(x)区间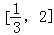 是增函数
是增函数
∴f'(x)≥0对
 恒成立,即不等式ax2+2x﹣1≥0对
恒成立,即不等式ax2+2x﹣1≥0对 恒成立.
恒成立.
即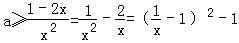 恒成立 故
恒成立 故
而当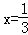 ,函数
,函数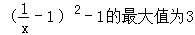 ,∴实数a的取值范围为a≥3.
,∴实数a的取值范围为a≥3.
【点评】本题考查了利用导数求函数极值以及函数单调性,属于常规题,必须掌握.
已知椭圆的中心在原点,焦点在x轴上,离心率为 ,长轴长为4
,长轴长为4 ,直线l:y=x+m交椭圆于不同的两点A,B.
,直线l:y=x+m交椭圆于不同的两点A,B.
(1)求椭圆的方程;
(2)求m的取值范围;
(3)若直线l不经过椭圆上的点M(4,1),求证:直线MA,MB的斜率互为相反数.
知识点:1.椭圆
【考点】直线与圆锥曲线的综合问题.
【专题】圆锥曲线中的最值与范围问题.
【分析】(Ⅰ)由已知条件推导出2a=4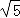 ,e=
,e=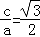 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(Ⅱ)将y=x+m代入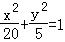 ,得5x2+8mx+4m2﹣20=0,利用根的判断式能求出m的取值范围.
,得5x2+8mx+4m2﹣20=0,利用根的判断式能求出m的取值范围.
(Ⅲ)设直线MA、MB的斜率分别为k1,k2,设A(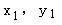 ),B(x2,y2),k1+k2=
),B(x2,y2),k1+k2=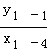 +
+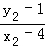 ,由此利用韦达定理能证明直线MA,MB的斜率互为相反数.
,由此利用韦达定理能证明直线MA,MB的斜率互为相反数.
【解答】解:(Ⅰ)椭圆的中心在原点,焦点在x轴上,离心率为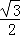 ,长轴长为4
,长轴长为4 ,
,
∴2a=4 ,e=
,e=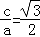 ,
,
解得a=2 ,c=
,c=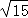 ,b=
,b= ,
,
∴椭圆方程为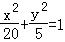 .…(4分)
.…(4分)
(Ⅱ)将y=x+m代入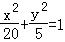 ,并整理,得:
,并整理,得:
5x2+8mx+4m2﹣20=0,
∵直线l:y=x+m交椭圆于不同的两点A,B,
∴△=(8m)2﹣20(4m2﹣20)>0,
解得﹣5<m<5,
∴m的取值范围是(﹣5,5).
(Ⅲ)设直线MA、MB的斜率分别为k1,k2,
设A(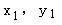 ),B(x2,y2),则由(Ⅱ)得x1+x2=﹣
),B(x2,y2),则由(Ⅱ)得x1+x2=﹣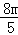 ,x1x2=
,x1x2= ,
,
k1+k2=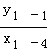 +
+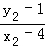 =
=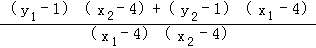 ,
,
∵分子=(x1+m﹣1)(x2﹣4)+(x2+m﹣1)(x1﹣ 4)
4)
=2x1x2+(m﹣5)(x1+x2)﹣8(m﹣1)
=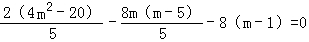 ,
,
∴k1+k2=0,
∴直线MA,MB的斜率互为相反数.
【点评】本题考查椭圆方程的求法,考查实数的取值范围的求法,考查两直线的斜率互为相反数的证明,解题时要注意根的判别式和韦达定理的合理运用.