设变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为
的最大值为
(A)3 (B)4 (C)18 (D)40
知识点:数学
C
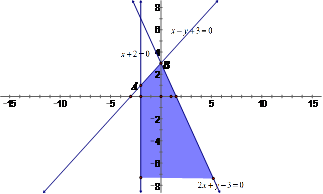
试题分析:不等式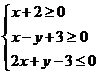 所表示的平面区域如下图所示,当
所表示的平面区域如下图所示,当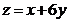 所表示直线经过点
所表示直线经过点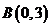 时,
时,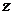 有最大值18.
有最大值18.
考点:线性规划.
阅读右边的程序框图,运行相应的程序,则输出S的值为
(A) (B)6 (C)14 (D)18
(B)6 (C)14 (D)18

知识点:数学
B
试题分析:模拟法:输入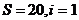 ;
;
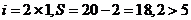 不成立;
不成立;
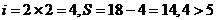 不成立
不成立
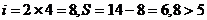 成立
成立
输出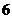 ,故选B.
,故选B.
考点:程序框图.
设 ,则“
,则“ ”是“
”是“ ”的
”的
(A)充分而不必要条件
(B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件
知识点:数学
A
试题分析:
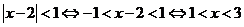 ,
,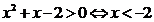 或
或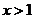 ,所以“
,所以“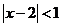 ”是
”是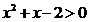 的充分不必要条件,故选A.
的充分不必要条件,故选A.
考点:充分条件与必要条件.
如图,在圆 中,
中, 是弦
是弦 的三等分点,弦
的三等分点,弦 分别经过点
分别经过点 .若
.若
 ,则线段
,则线段 的长为
的长为
(A) (B)3 (C)
(B)3 (C) (D)
(D)

知识点:数学
A
试题分析:由相交弦定理可知,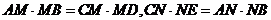 ,又因为
,又因为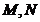 是弦
是弦 的三等分点,所以
的三等分点,所以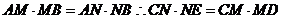 ,所以
,所以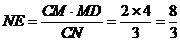 ,故选A.
,故选A.
考点:相交弦定理.
已知双曲线 的一条渐近线过点
的一条渐近线过点 ,且双曲线的一个焦点在抛物线
,且双曲线的一个焦点在抛物线 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为
(A) (B)
(B) (C)
(C) (D)
(D)
知识点:数学
D
试题分析:双曲线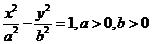 的渐近线方程为
的渐近线方程为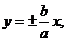 由点
由点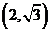 在渐近线上,所以
在渐近线上,所以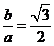 ,双曲线的一个焦点在抛物线
,双曲线的一个焦点在抛物线 准线方程
准线方程 上,所以
上,所以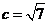 ,由此可解的
,由此可解的 ,所以双曲线方程为
,所以双曲线方程为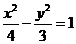 ,故选D.
,故选D.
考点:1.双曲线的标准方程及几何性质;2.抛物线的标准方程及几何性质.
已知定义在 上的函数
上的函数 (
( 为实数)为偶函数,记
为实数)为偶函数,记
 ,则
,则 的大小关系为
的大小关系为
(A) (B)
(B) (C)
(C) (D)
(D)
知识点:数学
C
试题分析:因为函数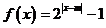 为偶函数,所以
为偶函数,所以 ,即
,即 ,所以
,所以
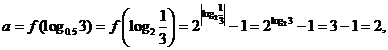
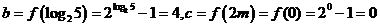
所以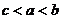 ,故选C.
,故选C.
考点:1.函数奇偶性;2.指数式、对数式的运算.
已知函数 函数
函数 ,其中
,其中 ,若函数
,若函数 恰有4个零点,则
恰有4个零点,则 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C) (D)
(D)
知识点:数学
D
试题分析:由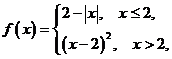 得
得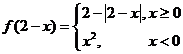 ,
,
所以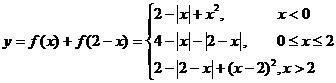 ,
,
即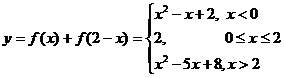
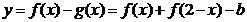 ,所以
,所以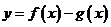 恰有4个零点等价于方程
恰有4个零点等价于方程
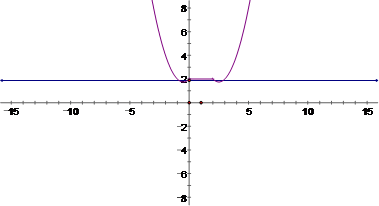
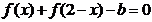 有4个不同的解,即函数
有4个不同的解,即函数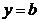 与函数
与函数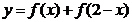 的图象的4个公共点,由图象可知
的图象的4个公共点,由图象可知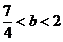 .
.
考点:1.求函数解析式;2.函数与方程;3.数形结合.
一个几何体的三视图如图所示(单位: ),则该几何体的体积为
),则该几何体的体积为  .
. 
知识点:数学
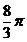
试题分析:由三视图可知,该几何体是中间为一个底面半径为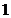 ,高为
,高为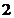 的圆柱,两端是底面半径为
的圆柱,两端是底面半径为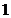 ,高为
,高为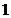 的圆锥,所以该几何体的体积
的圆锥,所以该几何体的体积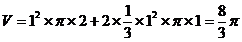 .
.
考点:1.三视图;2.旋转体体积.
在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知
,已知 的面积为
的面积为 ,
, 则
则 的值为 .
的值为 .
知识点:数学
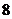
试题分析:
因为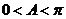 ,所以
,所以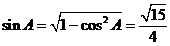 ,
,
又 ,解方程组
,解方程组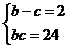 得
得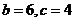 ,由余弦定理得
,由余弦定理得
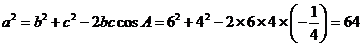 ,所以
,所以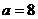 .
.
考点:1.同角三角函数关系;2.三角形面积公式;3.余弦定理.
在等腰梯形 中,已知
中,已知 ,动点
,动点 和
和 分别在线段
分别在线段 和
和 上,且,
上,且, 则
则 的最小值
的最小值
为 .
知识点:数学
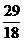
试题分析:
因为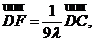
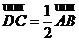 ,
,
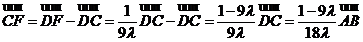 ,
,
 ,
,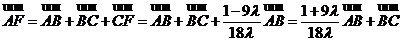 ,
,
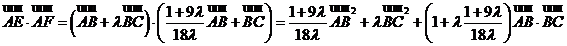
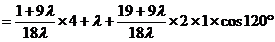
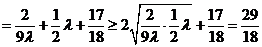
当且仅当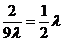 即
即 时
时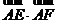 的最小值为
的最小值为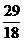 .
.
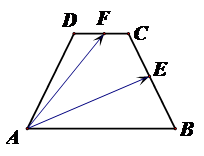
考点:1.向量的几何运算;2.向量的数量积;3.基本不等式.
已知函数 ,
,
(I)求 最小正周期;
最小正周期;
(II)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
知识点:数学
(I)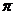 ; (II)
; (II)  ,
,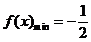 .
.
试题分析:
(I)利用两角和与差的正余弦公式及二倍角的正余弦公式化简函数的解析式,由三角函数性质可求最小正周期,
(II)先写出函数的单调区间,即可求函数的最大值与最小值。
试题解析:(I)由已知,有
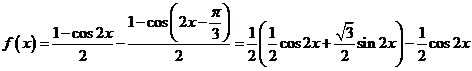
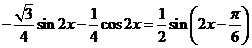
所以 的最小正周期
的最小正周期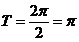
(II)因为 在区间
在区间 上是减函数,在区间
上是减函数,在区间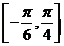 上是增函数.
上是增函数.
 所以
所以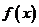 在区间
在区间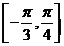 上的最大值为
上的最大值为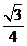 ,最小值为
,最小值为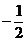 .
.
考点:1.两角和与差的正余弦公式;2.二倍角的正余弦公式;3.三角函数的图象与性质.
为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(I)设A为事件“选出的4人中恰有2 名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(II)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
知识点:数学
(I)  ;
;
(II) 随机变量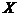 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
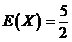
试题分析:(I)由古典概型计算公式直接计算即可; (II)先写出随机变量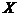 的所有可能值,求出其相应的概率,即可求概率分布列及期望.
的所有可能值,求出其相应的概率,即可求概率分布列及期望.
试题解析:(I)由已知,有
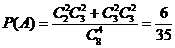
所以事件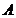 发生的概率为
发生的概率为 .
.
(II)随机变量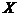 的所有可能取值为
的所有可能取值为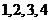
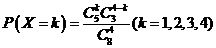
所以随机变量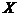 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
所以随机变量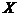 的数学期望
的数学期望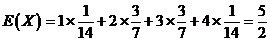
考点:1.古典概型;2.互斥事件;3.离散型随机变量的分布列与数学期望.
如图,在四棱柱 中,侧棱
中,侧棱
 ,
, ,
, ,
,
 ,且点M和N分别为
,且点M和N分别为 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求二面角 的正弦值;
的正弦值;
(III)设E为棱 上的点,若直线NE和平面ABCD所成角的正弦值为
上的点,若直线NE和平面ABCD所成角的正弦值为 ,求线段
,求线段 的长
的长

知识点:数学
(I)见解析; (II) 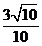 ; (III)
; (III) 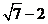 .
.
试题分析:以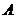 为原点建立空间直角坐标系(I)求出直线
为原点建立空间直角坐标系(I)求出直线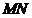 的方向向量与平面
的方向向量与平面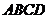 的法向量,两个向量的乘积等于
的法向量,两个向量的乘积等于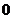 即可;(II)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦值即可;(III) 设
即可;(II)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦值即可;(III) 设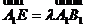 ,代入线面角公式计算可解出
,代入线面角公式计算可解出 的值,即可求出
的值,即可求出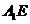 的长.
的长.
试题解析:如图,以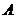 为原点建立空间直角坐标系,依题意可得
为原点建立空间直角坐标系,依题意可得 ,
,
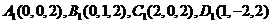 ,又因为
,又因为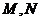 分别为
分别为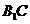 和
和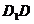 的中点,得
的中点,得 .
.

(I)证明:依题意,可得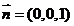 为平面
为平面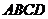 的一个法向量,
的一个法向量,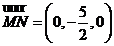 ,
,
由此可得,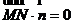 ,又因为直线
,又因为直线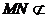 平面
平面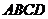 ,所以
,所以 平面
平面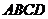
(II) ,设
,设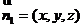 为平面
为平面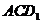 的法向量,则
的法向量,则
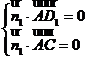 ,即
,即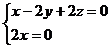 ,不妨设
,不妨设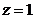 ,可得
,可得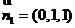 ,
,
设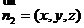 为平面
为平面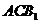 的一个法向量,则
的一个法向量,则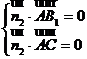 ,又
,又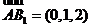 ,得
,得
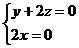 ,不妨设
,不妨设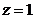 ,可得
,可得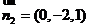
因此有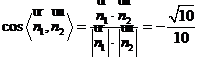 ,于是
,于是 ,
,
所以二面角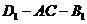 的正弦值为
的正弦值为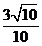 .
.
(III)依题意,可设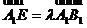 ,其中
,其中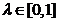 ,则
,则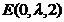 ,从而
,从而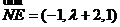 ,又
,又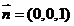 为平面
为平面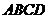 的一个法向量,由已知得
的一个法向量,由已知得
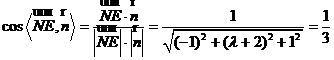 ,整理得
,整理得 ,
,
又因为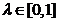 ,解得
,解得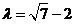 ,
,
所以线段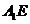 的长为
的长为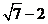 .
.
考点:1.直线和平面平行和垂直的判定与性质;2.二面角、直线与平面所成的角;3.空间向量的应用.
已知数列 满足
满足 ,且
,且
 成等差数列.
成等差数列.
(I)求q的值和 的通项公式;
的通项公式;
(II)设 ,求数列
,求数列 的前n项和.
的前n项和.
知识点:数学
(I) 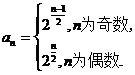 ; (II)
; (II) 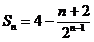 .
.
试题分析:(I)由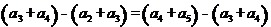 得
得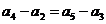 先求出
先求出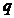 ,分
,分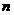 为奇数与偶数讨论即可;(II)求出数列
为奇数与偶数讨论即可;(II)求出数列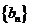 的通项公式,用错位相减法求和即可.
的通项公式,用错位相减法求和即可.
试题解析:(I) 由已知,有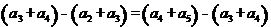 ,即
,即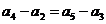 ,
,
所以 ,又因为
,又因为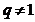 ,故
,故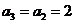 ,由
,由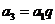 ,得
,得 ,
,
当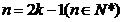 时,
时,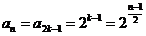 ,
,
当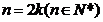 时,
时,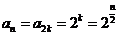 ,
,
所以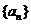 的通项公式为
的通项公式为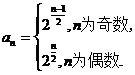
(II)由(I)得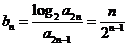 ,设数列
,设数列 的前
的前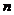 项和为
项和为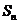 ,则
,则
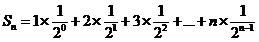 ,
,
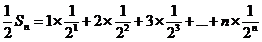
两式相减得
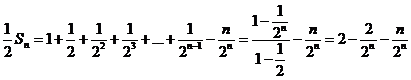
整理得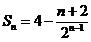
所以数列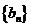 的前
的前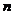 项和为
项和为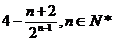
考点:1.等差中项定义;2.等比数列及前 项和公式.3.错位相减法.
项和公式.3.错位相减法.
19. (本小题满分14分)已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,点M在椭圆上且位于第一象限,直线FM被圆
,点M在椭圆上且位于第一象限,直线FM被圆 截得的线段的长为c,
截得的线段的长为c, .
.
(I)求直线FM的斜率;
(II)求椭圆的方程;
(III)设动点P在椭圆上,若直线FP的斜率大于 ,求直线OP(O为原点)的斜率的取值范围.
,求直线OP(O为原点)的斜率的取值范围.
知识点:数学
(I) 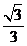 ; (II)
; (II) 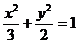 ;(III)
;(III) 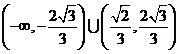 .
.
试题分析:(I) 由椭圆知识先求出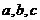 的关系,设直线直线
的关系,设直线直线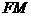 的方程为
的方程为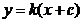 ,求出圆心到直线的距离,由勾股定理可求斜率
,求出圆心到直线的距离,由勾股定理可求斜率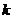 的值; (II)由(I)设椭圆方程为
的值; (II)由(I)设椭圆方程为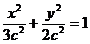 ,直线与椭圆方程联立,求出点
,直线与椭圆方程联立,求出点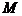 的坐标,由
的坐标,由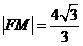 可求出
可求出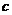 ,从而可求椭圆方程.(III)设出直线
,从而可求椭圆方程.(III)设出直线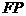 :
: ,与椭圆方程联立,求得
,与椭圆方程联立,求得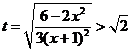 ,求出
,求出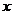 的范围,即可求直线
的范围,即可求直线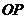 的斜率的取值范围.
的斜率的取值范围.
试题解析:(I) 由已知有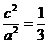 ,又由
,又由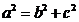 ,可得
,可得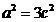 ,
,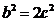 ,
,
设直线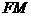 的斜率为
的斜率为 ,则直线
,则直线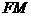 的方程为
的方程为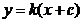 ,由已知有
,由已知有
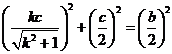 ,解得
,解得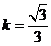 .
.
(II)由(I)得椭圆方程为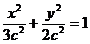 ,直线
,直线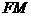 的方程为
的方程为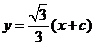 ,两个方程联立,消去
,两个方程联立,消去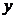 ,整理得
,整理得
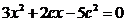 ,解得
,解得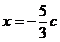 或
或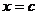 ,因为点
,因为点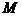 在第一象限,可得
在第一象限,可得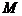 的坐标为
的坐标为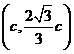 ,由
,由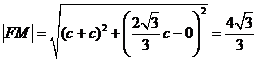 ,解得
,解得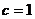 ,所以椭圆方程为
,所以椭圆方程为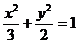
(III)设点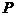 的坐标为
的坐标为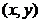 ,直线
,直线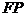 的斜率为
的斜率为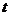 ,得
,得 ,即
,即
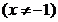 ,与椭圆方程联立
,与椭圆方程联立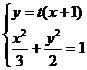 ,消去
,消去 ,整理得
,整理得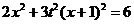 ,又由已知,得
,又由已知,得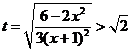 ,解得
,解得
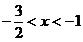 或
或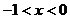 ,
,
设直线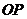 的斜率为
的斜率为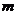 ,得
,得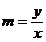 ,即
,即 ,与椭圆方程联立,整理可得
,与椭圆方程联立,整理可得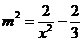 .
.
①当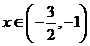 时,有
时,有 ,因此
,因此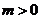 ,于是
,于是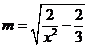 ,得
,得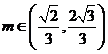
②当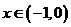 时,有
时,有 ,因此
,因此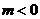 ,于是
,于是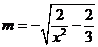 ,得
,得
综上,直线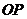 的斜率的取值范围是
的斜率的取值范围是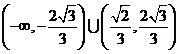
考点:1.椭圆的标准方程和几何性质;2.直线和圆的位置关系;3.一元二次不等式.
20. (本小题满分14分)已知函数 ,其中
,其中 .
.
(I)讨论 的单调性;
的单调性;
(II)设曲线 与
与 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数 ,都有
,都有 ;
;
(III)若关于 的方程
的方程 有两个正实根
有两个正实根 ,求证:
,求证: 
知识点:数学
(I) 当 为奇数时,
为奇数时,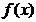 在
在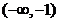 ,
, 上单调递减,在
上单调递减,在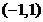 内单调递增;当
内单调递增;当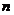 为偶数时,
为偶数时,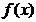 在
在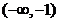 上单调递增,
上单调递增,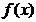 在
在 上单调递减. (II)见解析; (III)见解析.
上单调递减. (II)见解析; (III)见解析.
试题分析:
(I)求导,分 为奇数与偶数讨论其导数的符号及函数单调性即可;
为奇数与偶数讨论其导数的符号及函数单调性即可;
(II)设点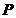 的坐标为
的坐标为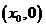 ,求出
,求出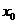 的值,构造函数
的值,构造函数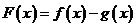 ,讨论函数
,讨论函数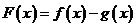 的单调性,可得
的单调性,可得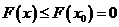 ,即可证出结论成立;
,即可证出结论成立;
(III)设方程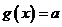 的根为
的根为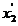 ,可证
,可证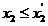 ,设曲线
,设曲线 在原点出的切线方程为
在原点出的切线方程为 ,设方程
,设方程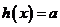 的根为
的根为 ,可得
,可得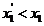 ,由此可得
,由此可得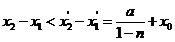 ,由
,由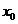 的取值范围,可证结论成立.
的取值范围,可证结论成立.
试题解析:(I)由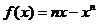 ,可得,
,可得,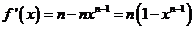 ,其中
,其中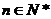 且
且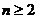 ,
,
下面分两种情况讨论:
(1)当 为奇数时:
为奇数时:
令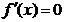 ,解得
,解得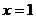 或
或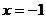 ,
,
当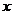 变化时,
变化时,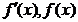 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
所以,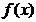 在
在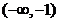 ,
, 上单调递减,在
上单调递减,在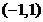 内单调递增.
内单调递增.
(2)当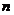 为偶数时,
为偶数时,
当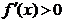 ,即
,即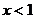 时,函数
时,函数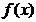 单调递增;
单调递增;
当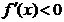 ,即
,即 时,函数
时,函数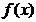 单调递减.
单调递减.
所以,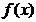 在
在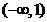 上单调递增,
上单调递增,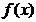 在
在 上单调递减.
上单调递减.
(II)证明:设点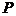 的坐标为
的坐标为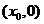 ,则
,则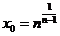 ,
,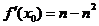 ,曲线
,曲线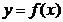 在点
在点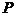 处的切线方程为
处的切线方程为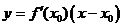 ,即
,即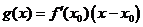 ,令
,令 ,即
,即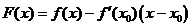 ,则
,则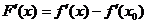
由于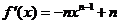 在
在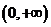 上单调递减,故
上单调递减,故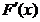 在
在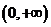 上单调递减,又因为
上单调递减,又因为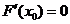 ,所以当
,所以当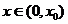 时,
时, 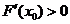 ,当
,当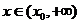 时,
时, ,所以
,所以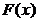 在
在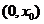 内单调递增,在
内单调递增,在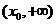 内单调递减,所以对任意的正实数
内单调递减,所以对任意的正实数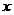 都有
都有 ,即对任意的正实数
,即对任意的正实数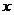 ,都有
,都有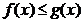 .
.
(III)证明:不妨设 ,由(II)知
,由(II)知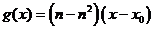 ,设方程
,设方程 的根为
的根为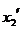 ,可得
,可得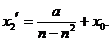 ,当
,当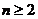 时,
时,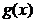 在
在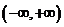 上单调递减,又由(II)知
上单调递减,又由(II)知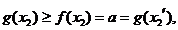 可得
可得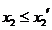 .
.
类似的,设曲线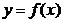 在原点处的切线方程为
在原点处的切线方程为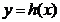 ,可得
,可得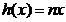 ,当
,当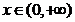 ,
,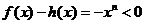 ,即对任意
,即对任意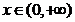 ,
,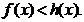
设方程 的根为
的根为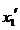 ,可得
,可得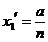 ,因为
,因为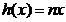 在
在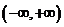 上单调递增,且
上单调递增,且
 ,因此
,因此 .
.
由此可得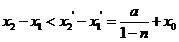 .
.
因为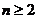 ,所以
,所以 ,故
,故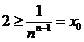 .
.
所以,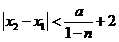 .
.
考点:1.导数的运算;2.导数的几何意义;3.利用导数研究函数性质、证明不等式.