设集合A={x|1<x<4},集合B={x|(x﹣3)(x+1)<0},则A∩B=( )
A.{x|﹣1<x<4} B.{x|﹣1<x<1} C.{x|1<x<3} D.{x|﹣1<x<3}
知识点:3.集合的基本运算
C
【考点】交集及其运算.
【专题】计算题;方程思想;定义法;集合.
【分析】利用不等式性质和集合定义求解.
【解答】解:(1)∵集合A={x|1<x<4},
集合B={x|(x﹣3)(x+1)<0}={x|﹣1<x<3},
∴A∩B={x|1<x<3}.
故选:C.
【点评】本题考查交集的求法,是基础题,解题时要认真审题,注意交集的定义的合理运用.
设i是虚数单位,则复数 =( )
=( )
A.1+i B.1﹣i C.﹣1﹣i D.﹣1+i
知识点:3.复数代数形式的四则运算
D
【考点】复数代数形式的乘除运算.
【专题】计算题;方程思想;数系的扩充和复数.
【分析】直接利用复数的除法与乘方运算法则化简求解即可.
【解答】解:复数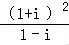 =
= =i(1+i)=﹣1+i.
=i(1+i)=﹣1+i.
故选:D.
【点评】本题考查复数的代数形式的混合运算,基本知识的考查.
已知命题P:∀x∈R,ex﹣x﹣1>0,则¬P是( )
A.∀x∈R,ex﹣x﹣1<0 B.∃x0∈R,e ﹣x0﹣1≤0
﹣x0﹣1≤0
C.∃x0∈R,e ﹣x0﹣1<0 D.∀x∈R,ex﹣x﹣1≤0
﹣x0﹣1<0 D.∀x∈R,ex﹣x﹣1≤0
知识点:7.全称量词与存在量词
B
【考点】命题的否定.
【专题】计算题;规律型;简易逻辑.
【分析】直接利用全称命题的否定是特称命题写出结果即可.
【解答】解:因为全称命题的否定是特称命题,所以,命题P:∀x∈R,ex﹣x﹣1>0,则¬P是∃x0∈R,e ﹣x0﹣1≤0.
﹣x0﹣1≤0.
故选:B.
【点评】本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.
下列函数中,满足“f(xy)=f(x)+f(y)”的单调递减函数是( )
A.f(x)=lnx B.f(x)=﹣x3 C.f(x)=log x D.f(x)=3﹣x
x D.f(x)=3﹣x
知识点:12.绝对值函数与分段函数及其他函数
C
【考点】抽象函数及其应用.
【专题】构造法;函数的性质及应用.
【分析】根据条件可知,对数函数符合条件,f(xy)=f(x)+f(y),再给出证明,最后根据函数的单调性确定选项.
【解答】解:对数函数符合条件f(xy)=f(x)+f(y),证明如下:
设f(x)=logax,其中,x>0,a>0且a≠1,
则f(xy)=logaxy=logax+logay=f(x)+f(y),
即对数函数f(x)=logax,符合条件f(xy)=f(x)+f(y),
同时,f(x)单调递减,则a∈(0,1),
综合以上分析,对数函数f(x)=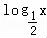 符合题意,
符合题意,
故答案为:C.
【点评】本题主要考查了抽象函数及其应用,涉及抽象函数的运算和函数模型的确定,以及对数的运算性质,属于基础题.
如图的程序图的算法思路中是一种古老而有效的算法﹣﹣辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )

A.10 B.12 C.13 D.16
知识点:1.算法与程序框图
B
【考点】程序框图.
【专题】计算题;图表型;试验法;算法和程序框图.
【分析】模拟程序框图的运行过程,该程序执行的是欧几里得辗转相除法,求出运算结果即可.
【解答】解:模拟程序框图的运行过程,如下;
m=30,n=42,30÷42=0,余数是30,r=30,不满足条件r=0,
m=42,n=30,42÷30=1,余数是12,r=12,不满足条件r=0,
m=30,n=12,30÷12=2,余数是6,r=6,不满足条件r=0,
m=12,n=6,12÷6=2,余数是0,r=0,满足条件r=0,退出循环,输出m的值为12.
故选:B.
【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的答案,是基础题.
为了得到函数y= sin4x﹣
sin4x﹣ cos4x的图象,可以将函数y=sin4x的图象( )
cos4x的图象,可以将函数y=sin4x的图象( )
A.向右平移 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位
C.向右平移 个单位 D.向左平移
个单位 D.向左平移 个单位
个单位
知识点:7.函数y=Asin(wx+@)+B
A
【考点】函数y=Asin(ωx+φ)的图象变换.
【专题】计算题;方程思想;转化思想;三角函数的图像与性质.
【分析】化简函数为一个角的一个三角函数的形式,然后平移平移关系判断选项即可.
【解答】解:函数y= sin4x﹣
sin4x﹣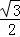 cos4x=sin(4x﹣
cos4x=sin(4x﹣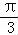 ),
),
∵sin(4x﹣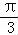 )=sin[4(x﹣
)=sin[4(x﹣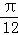 )],
)],
∴为了得到函数y= sin4x﹣
sin4x﹣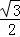 cos4x的图象,可以将函数y=sin4x的图象向右平移
cos4x的图象,可以将函数y=sin4x的图象向右平移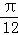 个单位.
个单位.
故选:A.
【点评】本题考查两角和与差的三角函数,三角函数的图象平移,考查计算能力.
某几何体的三视图如图所示,则此几何体的体积等于( )

A.45 B.36 C.30 D.6
知识点:2.空间几何体的三视图和直观图
C
【考点】由三视图求面积、体积.
【专题】数形结合;数形结合法;空间位置关系与距离.
【分析】该几何体为长方体切去一个三棱锥剩下的几何体.
【解答】解:由三视图可知该几何体为长方体ABCD﹣A1B1C1D1切去一个三棱锥B1﹣A1BC1剩下的几何体.
∴V=4×3×3﹣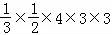 =30.
=30.
故选:C.
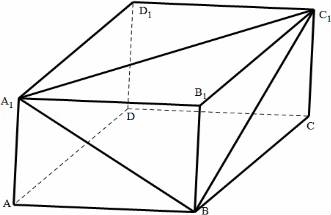
【点评】本题考查了空间几何体的三视图与体积计算,属于基础题.
春节前,某市一过江大桥上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的6秒内任一时刻等可能发生,然后每串彩灯以6秒内间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过3秒的概率是( )
A. B.
B. C.
C. D.
D.
知识点:3.几何概型
B
【考点】古典概型及其概率计算公式.
【专题】数形结合;数形结合法;概率与统计.
【分析】作出基本事件对应的平面区域和符合条件的平面区域,求出对应的几何度量.
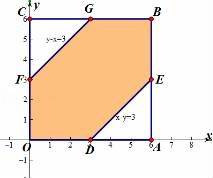
【解答】解:设两串彩灯分别在通电后x秒,y秒第一次闪亮,
则所有的可能情况对应的平面区域为正方形OABC,
作出直线x﹣y=3和直线y﹣x=3,则两灯在第一次闪亮时刻不超过3秒对应的平面区域为六边形ODEBGF,
∴P=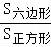 =
= =
=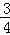 .
.
故选B.
【点评】本题考查了几何概型的概率计算,作出对应的平面区域是关键.
已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
A.16 B.8 C.8
C.8 D.18
D.18
知识点:3.抛物线
C
【考点】抛物线的简单性质.
【专题】综合题;转化思想;综合法;圆锥曲线的定义、性质与方程.
【分析】先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及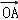 •
• =0,消元,最后将面积之和表示出来,探求最值问题.
=0,消元,最后将面积之和表示出来,探求最值问题.
【解答】解:设直线AB的方程为:x=ty+m,
点A(x1,y1),B(x2,y2),直线AB与x轴的交点为M(m,0),
x=ty+m代入y2=4x,可得y2﹣4ty﹣4m=0,
根据韦达定理有y1•y2=﹣4m,
∵OA⊥OB,
∴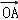 •
• =0,
=0,
∴x1•x2+y1•y2=0,从而(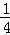 y1•
y1•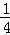 y2)2+y1•y2=0,
y2)2+y1•y2=0,
∵点A,B位于x轴的两侧,
∴y1•y2=﹣16,故m=4.
不妨令点A在x轴上方,则y1>0,
又F(1,0),
∴S△ABO+S△AFO=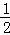 ×4×(y1﹣y2)+
×4×(y1﹣y2)+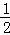 ×y1=
×y1=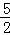 y1+
y1+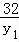
≥8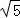 ,
,
当且仅当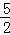 y1=
y1=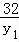 ,即y1=
,即y1=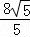 时,取“=”号,
时,取“=”号,
∴△ABO与△AFO面积之和的最小值是8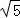 ,
,
故选:C.
【点评】求解本题时,应考虑以下几个要点:
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.
函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1) B.(﹣1,0)∪(1,+∞) C.(﹣∞,﹣1)∪(1,+∞) D.(﹣1,0)∪(0,1)
知识点:3.导数在研究函数中的应用
B
【考点】利用导数研究函数的单调性;函数的单调性与导数的关系.
【专题】数形结合;构造法;转化法;导数的概念及应用.
【分析】根据题意构造函数g(x)=xf(x),由求导公式和法则求出g′(x),结合条件判断出g′(x)的符号,即可得到函数g(x)的单调区间,根据f(x)奇函数判断出
g(x)是偶函数,将不等式进行转化,由图象求出不等式成立时x的取值范围.
【解答】解:设g(x)=xf(x),则g′(x)=xf′(x)+f(x),
∵当x<0时,xf′(x)+f(x)>0,
∴则当x<0时,g′(x)>0,
∴函数g(x)=xf(x)在(﹣∞,0)上为增函数,
∵函数f(x)是奇函数,∴g(﹣x)=(﹣x)f(﹣x)=(﹣x)[﹣f(x)]=xf(x)=g(x),
∴函数g(x)为定义域上的偶函数,
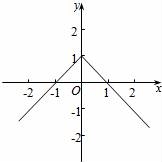
由f(1)=0得,g(1)=0,函数g(x)的图象大致如右图:
∵不等式f(x)<0⇔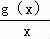 <0,
<0,
∴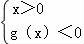 或
或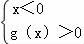 ,
,
由函数的图象得,﹣1<x<0或x>1,
∴使得f(x)<0成立的x的取值范围是:(﹣1,0)∪(1,+∞),
故选:B.
【点评】本题考查利用导数判断函数的单调性,由函数的奇偶性、单调性解不等式,考查构造函数法,转化思想和数形结合思想,属于综合题.
在(3﹣x)5的展开式中,含x3的项的系数是 (用数字作答)
知识点:3.二项式定理
﹣90
【考点】二项式系数的性质.
【专题】对应思想;转化法;二项式定理.
【分析】根据二项式展开式的通项公式,确定r的值,即可求出含x3的项的系数.
【解答】解:(3﹣x)5的展开式中,通项公式是Tr+1= •35﹣r•(﹣1)r•xr,
•35﹣r•(﹣1)r•xr,
令r=3,得含x3的项的系数是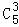 •32•(﹣1)3=﹣90.
•32•(﹣1)3=﹣90.
故答案为:﹣90.
【点评】本题考查了二项式展开式的通项公式的应用问题,是基础题目.
已知α∈(0, ),β∈(0,
),β∈(0, ),且cosα=
),且cosα= ,cos(α+β)=﹣
,cos(α+β)=﹣ ,则sinβ= .
,则sinβ= .
知识点:4.和角公式与倍(半)角公式
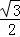
【考点】两角和与差的正弦函数.
【专题】转化思想;综合法;三角函数的求值.
【分析】由条件利用同角三角函数的基本关系、两角差的正弦公式,以及三角函数在各个象限中的符号,求得sinβ=sin[(α+β)﹣α]的值.
【解答】解:∵已知α∈(0,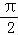 ),β∈(0,
),β∈(0,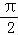 ),且cosα=
),且cosα=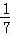 ,cos(α+β)=﹣
,cos(α+β)=﹣ ,
,
∴sinα= =
=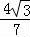 ,sin(α+β)=
,sin(α+β)=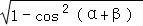 =
=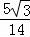 ,
,
则sinβ=sin[(α+β)﹣α]=sin(α+β)cosα﹣cos(α+β)sinα
=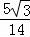 •
• ﹣(﹣
﹣(﹣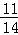 )•
)•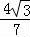 =
=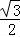 ,
,
故答案为: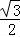 .
.
【点评】本题主要考查同角三角函数的基本关系、两角差的正弦公式,以及三角函数在各个象限中的符号,属于基础题.
已知实数x,y满足 ,则x2+y2的最大值为 .
,则x2+y2的最大值为 .
知识点:3.二元一次不等式(组)与简单的线性规划
13
【考点】简单线性规划的应用;简单线性规划.
【专题】计算题.
【分析】先根据条件画出可行域,z=x2+y2,再利用几何意义求最值,只需求出可行域内的点到原点距离的最值,从而得到z最大值即可.
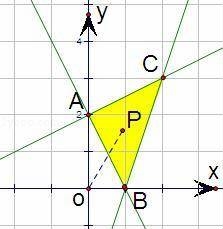
【解答】解:先根据约束条件画出可行域,
而z=x2+y2,
表示可行域内点到原点距离OP的平方,
点P在黄色区域里运动时,点P跑到点C时OP最大
当在点C(2,3)时,z最大,最大值为22+32=13,
故答案为:13
【点评】本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.解决时,首先要解决的问题是明白题目中目标函数的意义.
设四边形ABCD为平行四边形,| |=8,|
|=8,| |=3,若点M,N满足
|=3,若点M,N满足 =3
=3 ,
, =2
=2 ,则
,则 •
• = .
= .
知识点:4.平面向量的数量积(夹角、模)
9
【考点】平面向量数量积的运算.
【专题】对应思想;综合法;平面向量及应用.
【分析】用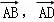 表示出
表示出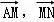 ,代入数量积计算.
,代入数量积计算.
【解答】解:∵ =3
=3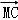 ,
,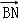 =2
=2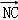 ,∴
,∴ =
=
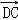 =
=
 ,
,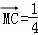
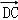 =
=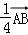 ,
,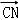 =
=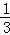
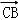 =﹣
=﹣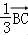 =﹣
=﹣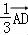 ,
,
∴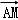 =
=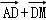 =
=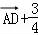
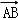 ,
,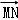 =
=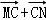 =
= .
.
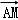 •
• =(
=(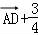
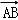 )•(
)•( )=
)=
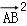 ﹣
﹣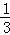
 =
= ×82﹣
×82﹣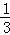 ×32=9.
×32=9.
故答案为:9.
【点评】本题考查了平面向量的数量积运算,是基础题.
设S为复数集C的非空子集.如果
(1)S含有一个不等于0的数;
(2)∀a,b∈S,a+b,a﹣b,ab∈S;
(3)∀a,b∈S,且b≠0, ∈S,那么就称S是一个数域.
∈S,那么就称S是一个数域.
现有如下命题:
①如果S是一个数域,则0,1∈S;
②如果S是一个数域,那么S含有无限多个数;
③复数集是数域;
④S={a+b |a,b∈Q,}是数域;
|a,b∈Q,}是数域;
⑤S={a+bi|a,b∈Z}是数域.
其中是真命题的有 (写出所有真命题的序号).
知识点:2.集合间的基本关系
①②③④
【考点】命题的真假判断与应用;元素与集合关系的判断;复数的基本概念.
【专题】简易逻辑;推理和证明;数系的扩充和复数.
【分析】根据已知中数域的概念,逐一分析5个命题的真假,综合讨论结果,可得答案.
【解答】解:由已知中(1)S含有一个不等于0的数;
(2)∀a,b∈S,a+b,a﹣b,ab∈S;
(3)∀a,b∈S,且b≠0,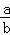 ∈S,那么就称S是一个数域.
∈S,那么就称S是一个数域.
令a=b≠0,
则a﹣b=0∈S;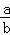 =1∈S,故①正确;
=1∈S,故①正确;
na∈S,n∈Z,故②正确;
复数集C满足3个条件,故复数集是数域,故③正确;
S={a+b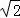 |a,b∈Q,}满足3个条件,故S是数域,故④正确;
|a,b∈Q,}满足3个条件,故S是数域,故④正确;
S={a+bi|a,b∈Z}不满足条件(3),故S不是数域,故⑤错误;
故答案为:①②③④
【点评】本题以命题的真假判断与应用为载体,考查了数域的概念,正确理解数域的概念,是解答的关键.
已知数列{an}满足a1=1,an+1=2an+1.
(1)求数列{an}的通项公式;
(2)令bn= n(an+1),求数列{bn}的前n项和Tn.
n(an+1),求数列{bn}的前n项和Tn.
知识点:6.数列的求和
【考点】数列的求和;数列递推式.
【专题】计算题;整体思想;综合法;等差数列与等比数列.
【分析】(1)通过对an+1=2an+1变形可知an+1+1=2(an+1),进而可知数列{an+1}是首项、公比均为2的等比数列,计算即得结论;
(2)通过(1)可知bn=n•2n﹣1,进而利用错位相减法计算即得结论.
【解答】解:(1)∵an+1=2an+1,
∴an+1+1=2(an+1),
又∵a1=1,
∴数列{an+1}是首项、公比均为2的等比数列,
∴an+1=2n,
∴an=﹣1+2n;
(2)由(1)可知bn=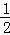 n(an+1)=
n(an+1)=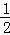 n•2n=n•2n﹣1,
n•2n=n•2n﹣1,
∴Tn=1•20+2•2+…+n•2n﹣1,
2Tn=1•2+2•22…+(n﹣1)•2n﹣1+n•2n,
错位相减得:﹣Tn=1+2+22…+2n﹣1﹣n•2n
=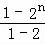 ﹣n•2n
﹣n•2n
=﹣1﹣(n﹣1)•2n,
于是Tn=1+(n﹣1)•2n.
【点评】本题考查数列的通项及前n项和,考查运算求解能力,考查错位相减法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.
某高校文学院和理学院的学生组队参加大学生电视辩论赛,文学院推荐了2名男生,3名女生,理学院推荐了4名男生,3名女生,文学院和理学院所推荐的学生一起参加集训,由于集训后学生水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队.
(1)求文学院至少有一名学生入选代表队的概率;
(2)某场比赛前,从代表队的6名学生在随机抽取4名参赛,记X表示参赛的男生人数,求X的分布列与数学期望.
知识点:9.离散型随机变量的分布列、均值与方差
【考点】离散型随机变量的期望与方差;列举法计算基本事件数及事件发生的概率;离散型随机变量及其分布列.
【专题】应用题;方程思想;综合法;概率与统计.
【分析】(1)求出文学院至少有一名学生入选代表队的对立事件的概率,然后求解概率即可;
(2)求出X表示参赛的男生人数的可能值,求出概率,得到X的分布列,然后求解数学期望.
【解答】解:(1)由题意,参加集训的男、女学生共有6人,参赛学生全从理学院中抽出(等价于文学院中没有学生入选代表队)的概率为: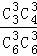 =
=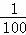 ,因此文学院至少有一名学生入选代表队的概率为:1﹣
,因此文学院至少有一名学生入选代表队的概率为:1﹣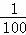 =
=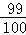 ;
;
(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛,X表示参赛的男生人数,
则X的可能取值为:1,2,3,
P(X=1)=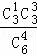 =
=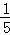 ,P(X=2)=
,P(X=2)=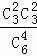 =
=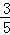 ,P(X=3)=
,P(X=3)=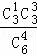 =
=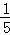 .
.
X的分布列:
X | 1 | 2 | 3 |
P |
|
|
|
和数学期望EX=1×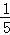 +2×
+2×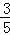 +3×
+3×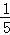 =2.
=2.
【点评】本题考查离散型随机变量的分布列,期望的求法,考查古典概型概率的求法,考查分析问题解决问题的能力.
已知函数f(x)=sinx(sinx+ cosx).
cosx).
(1)求f(x)的最小正周期和最大值;
(2)在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,若f( )=1,a=2
)=1,a=2 ,求三角形ABC面积的最大值.
,求三角形ABC面积的最大值.
知识点:4.和角公式与倍(半)角公式
【考点】三角函数中的恒等变换应用;正弦函数的图象.
【专题】函数思想;综合法;三角函数的求值;解三角形.
【分析】(1)利用二倍角公式化简f(x);
(2)求出A,根据余弦定理和基本不等式得出bc的最大值,代入面积公式即可.
【解答】解:(1)f(x)=sin2x+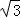 sinxcosx=
sinxcosx= ﹣
﹣ cos2x+
cos2x+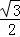 sin2x=sin(2x﹣
sin2x=sin(2x﹣ )
)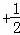 .
.
∴f(x)的最小正周期T=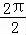 =π,f(x)的最大值是
=π,f(x)的最大值是 .
.
(2)∵f(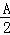 )=sin(A﹣
)=sin(A﹣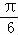 )+
)+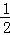 =1,∴sin(A﹣
=1,∴sin(A﹣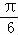 )=
)=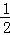 ,∴A=
,∴A= .
.
∵a2=b2+c2﹣2bccosA,∴12=b2+c2﹣bc,∴b2+c2=12+bc≥2bc,∴bc≤12.
∴S=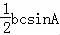 =
= bc≤3
bc≤3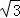 .
.
∴三角形ABC面积的最大值是3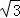 .
.
【点评】本题考查了三角函数的恒等变换,三角函数的性质,解三角形,属于中档题.
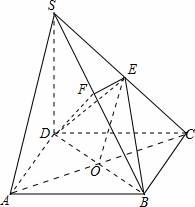
如图,在四棱锥S﹣ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
(1)求证:SA∥平面BDE;
(2)求证SB⊥平面DEF;
(3)求二面角C﹣SB﹣D的余弦值.

知识点:5.直线、平面平行的判定及其性质
【考点】二面角的平面角及求法;直线与平面平行的判定;直线与平面垂直的判定.
【专题】数形结合;空间角;立体几何.
【分析】(1)连接AC交BD于点O,连接OE.然后利用三角形中位线的性质可得OE∥SA,再由线面平行的判定定理证得SA∥平面BDE;
(2)由SD=DC,E是SC的中点可得DE⊥SC,再由面面垂直的判定和性质得到BC⊥平面SDC,从而得到BC⊥DE,进一步得到SB⊥DE,结合已知EF⊥SB,由线面垂直的判定得结论;
(3)根据二面角的定义得到∠EFD是二面角C﹣SB﹣D的平面角,根据三角形的边角关系进行求解即可.
【解答】(1)证明:如图,
连接AC交BD于点O,连接OE.
∵点O、E分别为AC、SC的中点,
∴OE∥SA,又OE⊂平面BDE,SA⊄平面BDE,
∴SA∥平面BDE;
(2)证明:∵SD=DC,E是SC的中点,∴DE⊥SC,
又SD⊥底面ABCD,∴平面SDC⊥平面ABCD,
∵底面ABCD是矩形,∴BC⊥平面SDC,
∴BC⊥DE,
又SC∩BC=C,∴DE⊥平面SBC,
又SB⊂平面SBC,∴SB⊥DE,
又EF⊥SB,
EF∩ED=E,
∴SB⊥平面EFD;
(3)∵EF⊥SB,SB⊥平面EFD,
∴∠EFD是二面角C﹣SB﹣D的平面角,
设AD=1,则SD=CD=2,
则SC=2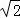 ,SB=
,SB=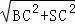 =3,BD=
=3,BD=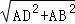 =
=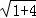 =
=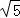 ,DE=
,DE=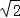 ,
,
在三角形SDB中,SB•DF=SD•BD,即DF= =
=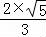 =
=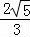 ,
,
在三角形SBC中,sinCSB=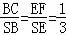 ,即EF=
,即EF=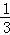 SE=
SE=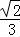 ,
,
在三角形DEF中,cosEFD=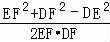 =
=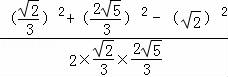 =
=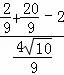 =
=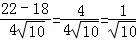 =
=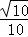 ,
,
即二面角C﹣SB﹣D的余弦值是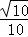 .
.
【点评】本题综合考查空间中线线、线面的位置关系和空间中角的计算,涉及二面角的平面角,传统方法和坐标向量法均可,考查的知识面较广,综合性较强,运算量较大.
已知圆F1:(x+1)2+y2=1,圆F2:(x﹣1)2+y2=25,动圆P与圆F1外切并且与圆F2内切,动圆圆心P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)若曲线C与x轴的交点为A1,A2,点M是曲线C上异于点A1,A2的点,直线A1M与A2M的斜率分别为k1,k2,求k1k2的值.
(Ⅲ)过点(2,0)作直线l与曲线C交于A,B两点,在曲线C上是否存在点N,使 +
+ =
= ?若存在,请求出直线l的方程;若不存在,请说明理由.
?若存在,请求出直线l的方程;若不存在,请说明理由.
知识点:4.直线与圆的位置关系
【考点】直线与圆锥曲线的关系;轨迹方程.
【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)通过设P(x,y)、动圆P的比较为r,利用圆与圆的位置关系可知|PF1|=1+r、|PF2|=5﹣r,进而化简可知动圆圆心P的轨迹是以F1(﹣1,0)、F2(1,0)为焦点、长轴长为6的椭圆,计算即得结论;
(Ⅱ)通过(I)可知A1(﹣3,0)、A2(3,0),通过设M(x,y),利用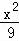 +
+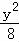 =及k1k2=
=及k1k2=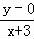 •
•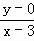 化简计算即得结论;
化简计算即得结论;
(Ⅲ)通过设过点(2,0)的直线l方程为x=my+2,并与曲线C方程联立,利用韦达定理及N(x1+x2,y1+y2)在曲线C上化简计算即得结论.
【解答】解:(Ⅰ)依题意,F1(﹣1,0),F2(1,0),
设P(x,y),动圆P的比较为r,则|PF1|=1+r,|PF2|=5﹣r,
∴|PF1|+|PF2|=6,
∴动圆圆心P的轨迹是以F1(﹣1,0)、F2(1,0)为焦点,长轴长为6的椭圆,
则b2=a2﹣c2=9﹣1=8,
于是曲线C的方程为: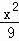 +
+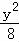 =1;
=1;
(Ⅱ)由(I)可知A1(﹣3,0),A2(3,0),
设M(x,y),则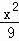 +
+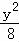 =1,
=1,
于是k1k2=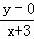 •
•
=
=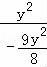
=﹣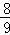 ;
;
(Ⅲ)结论:在曲线C上存在点N,使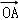 +
+ =
=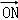 .
.
理由如下:
设过点(2,0)的直线l方程为:x=my+2,
联立直线l与曲线C的方程,消去x,整理得:
(9+8m2)y2+32my﹣40=0,
设A(x1,y1),B(x2,y2),则y1+y2=﹣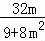 ,y1y2=﹣
,y1y2=﹣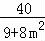 ,
,
∵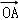 +
+ =
= ,
,
∴N(x1+x2,y1+y2)在曲线C上,
∴ +
+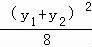 =1,
=1,
又∵x1+x2=m(y1+y2)+4=4﹣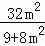 =
=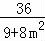 ,
,
∴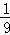 •
•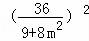 +
+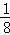 •
• =1,
=1,
整理得:9+8m2=16,
解得:m=±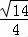 ,
,
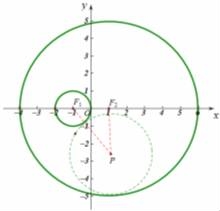
于是在曲线C上存在点N,使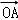 +
+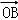 =
=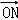 .
.
【点评】本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.
设函数f(x)= +k(
+k( +lnx)(k为常数).
+lnx)(k为常数).
(1)当k=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当k≥0时,求函数f(x)的单调区间;
(3)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
知识点:3.导数在研究函数中的应用
【考点】利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.
【专题】计算题;作图题;数形结合;导数的概念及应用;导数的综合应用.
【分析】(1)求导f′(x)=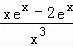 ,从而可得f(1)=e,f′(1)=﹣e,从而确定切线方程;
,从而可得f(1)=e,f′(1)=﹣e,从而确定切线方程;
(2)求导f′(x)=(x﹣2)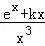 ,从而判断导数的正负以确定函数的单调性;
,从而判断导数的正负以确定函数的单调性;
(3)求导f′(x)=(x﹣2)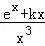 ,从而可得h(x)=ex+kx在(0,2)内存在两个零点,从而化为y=ex与y=﹣kx的图象在(0,2)内有两个交点,从而利用数形结合求解.
,从而可得h(x)=ex+kx在(0,2)内存在两个零点,从而化为y=ex与y=﹣kx的图象在(0,2)内有两个交点,从而利用数形结合求解.
【解答】解:(1)当k=0时,f(x)=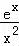 ,f′(x)=
,f′(x)=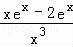 ,
,
故f(1)=e,f′(1)=﹣e,
故曲线y=f(x)在点(1,f(1))处的切线方程为y﹣e=﹣e(x﹣1),
即切线方程为:ex+y﹣2e=0;
(2)f(x)=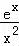 +k(
+k(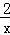 +lnx)的定义域为(0,+∞),
+lnx)的定义域为(0,+∞),
f′(x)=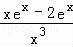 +k(﹣
+k(﹣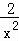 +
+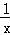 )=(x﹣2)
)=(x﹣2)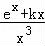 ,
,
∵k≥0,且x∈(0,+∞),∴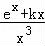 >0,
>0,
故当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0;
故函数f(x)的单调减区间为(0,2),单调增区间为(2,+∞);
(3)由(2)知,f′(x)=(x﹣2)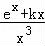 ,
,
∵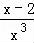 <0在(0,2)上恒成立,
<0在(0,2)上恒成立,
又∵函数f(x)在(0,2)内存在两个极值点,
∴h(x)=ex+kx在(0,2)内存在两个零点,
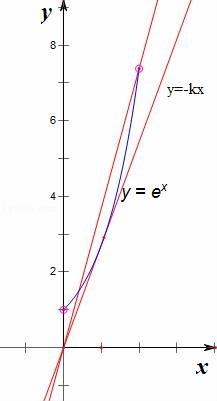
∴y=ex与y=﹣kx的图象在(0,2)内有两个交点,
作y=ex与y=﹣kx的图象如图,
相切时,设切点为(x,ex),
则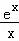 =ex,
=ex,
故x=1;
故k1=e;
k2=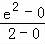 =
=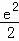 ,
,
故e<﹣k<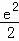 ,
,
故﹣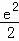 <k<﹣e.
<k<﹣e.
【点评】本题考查了导数的综合应用及数形结合的思想应用,同时考查了导数的几何意义的应用.