在等差数列{an}中,a1=21,a7=18,则公差d=( )
A. B.
B. C.﹣
C.﹣ D.﹣
D.﹣
知识点:2.等差数列及其性质
D
【考点】等差数列的通项公式.
【专题】等差数列与等比数列.
【分析】利用等差数列的通项公式即可得出.
【解答】解:由等差数列的通项公式可得a7=a1+6d,∴18=21+6d,解得d=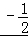 .
.
故选:D.
【点评】本题考查了等差数列的通项公式,属于基础题.
在△ABC中,若sinA=cosB= ,则∠C=( )
,则∠C=( )
A.45° B.60° C.30° D.90°
知识点:5.三角函数的求值、化简与证明
D
【考点】运用诱导公式化简求值.
【专题】转化思想;综合法;三角函数的求值.
【分析】由条件求得B的值,再求得A的值,利用三角形的内角和公式求得C的值.
【解答】解:△ABC中,若sinA=cosB=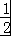 ,则∠B=60°,∴∠A=30°,∠C=90°,
,则∠B=60°,∴∠A=30°,∠C=90°,
故选:D.
【点评】本题主要考查特殊角的三角函数的值,三角形的内角和公式,属于基础题.
已知a,b为非零实数,且a<b,则下列命题成立的是( )
A.a2<b2 B.a2b<ab2 C.2a﹣2b<0 D. >
>
知识点:1.不等式关系与不等式
C
【考点】不等式的基本性质.
【专题】计算题.
【分析】根据函数y=2x在定义域R上是个增函数,可以得到2a<2b . 通过举反例说明A、B、D不正确.
【解答】解:A 不正确,如 a=﹣3,b=﹣1,显然a2<b2 不成立.
B 不成立,如a=﹣3,b=1时,显然a2b<ab2 不成立.
D不正确,如 a=﹣3,b=1时, >
> 显然不成立.
显然不成立.
∵函数y=2x在定义域R上是个增函数,∴2a<2b,∴2a﹣2b<0,
故选 C.
【点评】本题考查不等式的基本性质,利用了函数y=2x 在定义域 R 上是个增函数这个结论.
设等比数列{an}的公比q=2,前n项和为Sn,则 =( )
=( )
A.2 B.4 C. D.
D.
知识点:5.等比数列的前n项和
C
【考点】等比数列的前n项和.
【专题】计算题;等差数列与等比数列.
【分析】由等比数列的通项公式和求和公式,代入要求的式子化简可得.
【解答】解:由等比数列的求和公式和通项公式可得: =
=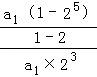 =
=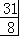 ,
,
故选:C.
【点评】本题考查等比数列的通项公式和求和公式,属基础题.
如果方程x2+(m﹣1)x+m2﹣2=0的两个实根一个小于﹣1,另一个大于1,那么实数m的取值范围是( )
A.﹣ <m<
<m< B.﹣2<m<0 C.﹣2<m<1 D.0<m<1
B.﹣2<m<0 C.﹣2<m<1 D.0<m<1
知识点:13.函数与方程
D
【考点】一元二次方程的根的分布与系数的关系.
【专题】函数的性质及应用.
【分析】令f(x)=x2+(m﹣1)x+m2﹣2,则由题意利用二次函数的性质求得实数m的取值范围.
【解答】解:令f(x)=x2+(m﹣1)x+m2﹣2,则由题意可得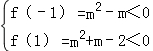 ,
,
求得 0<m<1,
故选:D.
【点评】本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.
已知数列{an}是等差数列,数列{bn}是等比数列,其公比q≠1,且bi>0(i=1,2,3,…),若a1=b1,a11=b11,则( )
A.a6=b6 B.a6>b6 C.a6<b6 D.a6>b6或a6<b6
知识点:2.等差数列及其性质
B
【考点】等比数列的通项公式;等差数列的通项公式.
【专题】计算题.
【分析】由题意可得 a1+a11=b1+b11=2a6,再由 b1+b11>2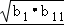 =2b6,从而得出结论.
=2b6,从而得出结论.
【解答】解:由题意可得 a1+a11=b1+b11=2a6.
∵公比q≠1,bi>0,∴b1+b11>2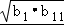 =2b6,
=2b6,
∴2a6>2b6,即 a6>b6,
故选B.
【点评】本题主要考查等差数列的定义和性质,等比数列的定义和性质,基本不等式的应用,属于基础题.
平面区域如图所示,若使目标函数z=x+ay(a>0)取得最大值的最优解有无穷多个,则a的值是( )

A. B.1 C.
B.1 C. D.4
D.4
知识点:3.二元一次不等式(组)与简单的线性规划
A
【考点】正切函数的图象.
【专题】三角函数的图像与性质.
【分析】对目标函数z=x+ay(a>0)变形为y=﹣ x+
x+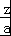 ,依题意可得﹣
,依题意可得﹣ =kAB=﹣
=kAB=﹣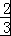 ,于是可求得a的值.
,于是可求得a的值.
【解答】解:∵z=x+ay(a>0),
∴y=﹣ x+
x+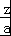 ,
,
∵目标函数z=x+ay(a>0)取得最大值的最优解有无穷多个,
∴﹣ =kAB=
=kAB=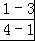 =﹣
=﹣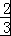 ,
,
∴a=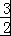 ,
,
故选:A.
【点评】本题考查线性规划问题,依题意得到得﹣ =kAB=﹣
=kAB=﹣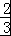 是关键,考查转化思想.
是关键,考查转化思想.
等差数列{an}的公差d<0,且a12=a112,则数列{an}的前n项和Sn取得最大值时的项数n是( )
A.5 B.6 C.5或6 D.6或7
知识点:3.等差数列的前n项和
C
【考点】等差数列的前n项和;等差数列的通项公式.
【专题】计算题.
【分析】由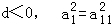 ,知a1+a11=0.由此能求出数列{an}的前n项和Sn取得最大值时的项数n.
,知a1+a11=0.由此能求出数列{an}的前n项和Sn取得最大值时的项数n.
【解答】解:由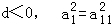 ,
,
知a1+a11=0.
∴a6=0,
故选C.
【点评】本题主要考查等差数列的性质,求和公式.要求学生能够运用性质简化计算.
若关于x的不等式2x2﹣8x﹣4﹣a>0在1<x<4内有解,则实数a的取值范围是( )
A.a<﹣4 B.a>﹣4 C.a>﹣12 D.a<﹣12
知识点:2.一元二次不等式及不等式的解法
A
【考点】一元二次不等式的应用.
【专题】计算题.
【分析】先将原不等式2x2﹣8x﹣4﹣a>0化为:a<2x2﹣8x﹣4,设y=2x2﹣8x﹣4,y=a,只须a小于y=2x2﹣8x﹣4在1<x<4内的最大值时即可,从而求得实数a的取值范围.
【解答】解:原不等式2x2﹣8x﹣4﹣a>0化为:a<2x2﹣8x﹣4,
只须a小于y=2x2﹣8x﹣4在1<x<4内的最大值时即可,
∵y=2x2﹣8x﹣4在1<x<4内的最大值是﹣4.
则有:a<﹣4.
故选A.
【点评】本小题主要考查一元二次不等式的应用等基础知识,考查等价化归与转化思想.属于基础题.
△ABC中,AB= ,AC=1,∠B=30°,则△ABC的面积等于( )
,AC=1,∠B=30°,则△ABC的面积等于( )
A. B.
B. C.
C. D.
D.
知识点:9.正弦定理和余弦定理(解三角形)
D
【考点】解三角形.
【专题】计算题.
【分析】由AB,AC及cosB的值,利用余弦定理即可列出关于BC的方程,求出方程的解即可得到BC的长,然后利用三角形的面积公式,由AB,BC以及sinB的值即可求出△ABC的面积.
【解答】解:由AB=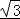 ,AC=1,cosB=cos30°=
,AC=1,cosB=cos30°=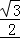 ,
,
根据余弦定理得:AC2=AB2+BC2﹣2AB•BCcosB,即1=3+BC2﹣3BC,
即(BC﹣1)(BC﹣2)=0,解得:BC=1或BC=2,
当BC=1时,△ABC的面积S= AB•BCsinB=
AB•BCsinB= ×
×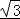 ×1×
×1×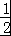 =
=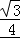 ;
;
当BC=2时,△ABC的面积S=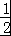 AB•BCsinB=
AB•BCsinB=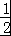 ×
×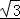 ×2×
×2×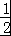 =
=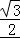 ,
,
所以△ABC的面积等于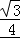 或
或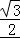 .
.
故选D
【点评】此题考查学生灵活运用余弦定理及三角形的面积公式化简求值,是一道中档题.
已知a>0,b>0, ,若不等式2a+b≥4m恒成立,则m的最大值为( )
,若不等式2a+b≥4m恒成立,则m的最大值为( )
A.10 B.9 C.8 D.7
知识点:4.基本不等式
B
【考点】基本不等式在最值问题中的应用.
【专题】计算题;不等式的解法及应用.
【分析】利用2a+b=4(2a+b)(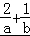 ),结合基本不等式,不等式2a+b≥4m恒成立,即可求出m的最大值.
),结合基本不等式,不等式2a+b≥4m恒成立,即可求出m的最大值.
【解答】解:∵a>0,b>0,
∴2a+b>0
∵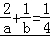 ,
,
∴2a+b=4(2a+b)(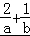 )=4(5+
)=4(5+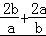 )≥36,
)≥36,
∵不等式2a+b≥4m恒成立,
∴36≥4m,
∴m≤9,
∴m的最大值为9,
故选:B.
【点评】本题主要考查了恒成立问题与最值的求解的相互转化,解题的关键是配凑基本不等式成立的条件.
设等差数列{an}(n∈N+)的前n项和为Sn,该数列是单调递增数列,若S4≥10,S5≤15,则a4的取值范围是( )
A.( ] B.(
] B.( ] C.(﹣∞,4] D.(3,+∞)
] C.(﹣∞,4] D.(3,+∞)
知识点:3.等差数列的前n项和
A
【考点】等差数列的性质;数列的函数特性.
【专题】计算题.
【分析】根据等差数列是一个等差数列,给出两个前n项和,写出求前n项和的公式,根据不等式的基本性质和等差数列的性质整理出结果.
【解答】解:∵等差数列{an是单调递增数列,
若S4≥10,S5≤15,
∴4a1+6d≥10 ①
5a1+10d≤15 ②
(﹣1)①+②a5≤5
0<d≤1,
由②得,a3≤3,
∴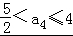
故选A.
【点评】本题考查等差数列的性质和不等式的性质,本题解题的关键是列出不等式组,解出要用的值的范围,本题是一个简单的综合题目.
设公比为q的等比数列{an}的前n项和为Sn,若Sn+1、Sn、Sn+2成等差数列,则q= .
知识点:5.等比数列的前n项和
﹣2
【考点】等比数列的通项公式.
【专题】等差数列与等比数列.
【分析】通过记等比数列{an}的通项为an,利用Sn﹣Sn+1=Sn+2﹣Sn即﹣an•q=an•q+an•q2,计算即得结论.
【解答】解:记等比数列{an}的通项为an,
则an+1=an•q,an+2=an•q2,
又∵Sn+1、Sn、Sn+2成等差数列,
∴Sn﹣Sn+1=Sn+2﹣Sn,
即﹣an•q=an•q+an•q2,
∴q2+2q=0,
∴q=﹣2,
故答案为:﹣2.
【点评】本题考查等差数列、等比数列的性质,注意解题方法的积累,属于中档题.
在约束条件 下,目标函数z=ax+by(a>0,b>0)的最大值为1,则ab的最大值等于 .
下,目标函数z=ax+by(a>0,b>0)的最大值为1,则ab的最大值等于 .
知识点:3.二元一次不等式(组)与简单的线性规划
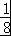
【考点】简单线性规划.
【专题】压轴题;数形结合;不等式的解法及应用.
【分析】画出满足约束条件的可行域,再根据目标函数z=ax+by(a>0,b>0)的最大值为1,求出a,b的关系式,利用基本不等式,可求ab的最大值.
【解答】解:约束条件对应的平面区域如图
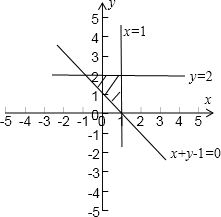
3个顶点是(1,0),(1,2),(﹣1,2),
由图易得目标函数在(1,2)取最大值1,
此时a+2b=1,
∵a>0,b>0,∴由不等式知识可得:1≥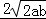
∴ab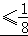 ,当且仅当a=
,当且仅当a=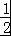 ,b=
,b=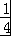 时,取等号
时,取等号
∴ab的最大值等于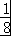
故答案为: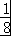
【点评】本题考查线性规划知识,考查数形结合的数学思想.用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键.
如图,在△ABC中,∠ABC=90°, ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
(Ⅰ)若 ,求PA;
,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.

知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;正弦定理.
【专题】解三角形.
【分析】(I)在Rt△PBC,利用边角关系即可得到∠PBC=60°,得到∠PBA=30°.在△PBA中,利用余弦定理即可求得PA.
(II)设∠PBA=α,在Rt△PBC中,可得PB=sinα.在△PBA中,由正弦定理得 ,即
,即 ,化简即可求出.
,化简即可求出.
【解答】解:(I)在Rt△PBC中,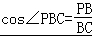 =
=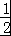 ,∴∠PBC=60°,∴∠PBA=30°.
,∴∠PBC=60°,∴∠PBA=30°.
在△PBA中,由余弦定理得PA2=PB2+AB2﹣2PB•ABcos30°=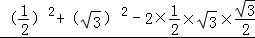 =
=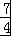 .
.
∴PA=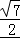 .
.
(II)设∠PBA=α,在Rt△PBC中,PB=BCcos(90°﹣α)=sinα.
在△PBA中,由正弦定理得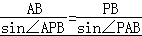 ,即
,即 ,
,
化为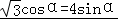 .∴
.∴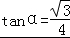 .
.
【点评】熟练掌握直角三角形的边角关系、正弦定理和余弦定理是解题的关键.
已知数列{an}满足 数列{bn}的前n项和Sn=n2+2n.
数列{bn}的前n项和Sn=n2+2n.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
知识点:6.数列的求和
【考点】数列的求和;等差数列的通项公式;等比数列的通项公式;数列递推式.
【专题】计算题;等差数列与等比数列.
【分析】(1)利用等比数列的通项公式可求an,利用n≥2时,bn=sn﹣sn﹣1,b1=s1可求bn
(2)由(1)可知求cn=anbn,然后利用错位相减求和方法即可求解
【解答】解(1)∵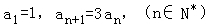
∴数列{an}是以1为首项以3为公办的等比数列
∴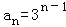
∵Sn=n2+2n
当n≥2时,bn=sn﹣sn﹣1=n2+2n﹣(n﹣1)2+2(n﹣1)=2n+1
当n=1时,b1=s1=3适合上式
∴bn=2n+1
(2)由(1)可知,cn=anbn=(2n+1)•3n﹣1
∴Tn=3•1+5•3+7•32+…+(2n+1)•3n﹣1
3Tn=3•3+5•32+…+(2n+1)•3n
两式相减可得,﹣2Tn=3+2(3+32+33+…+3n﹣1)﹣(2n+1)•3n
=3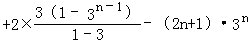
=2n•3n
∴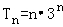
【点评】本题主要考查了利用 数列的递推公式求解数列的通项及错位相减求和方法的应用,要注意掌握该求和方法
已知关于x的不等式ax2+5x+c>0的解集为{x| <x<
<x< },
},
(Ⅰ)求a,c的值;
(Ⅱ)解关于x的不等式ax2+(ac+b)x+bc≥0.
知识点:2.一元二次不等式及不等式的解法
【考点】一元二次不等式的解法.
【专题】不等式的解法及应用.
【分析】(Ⅰ)根据韦达定理即可求出a,c的值,
(Ⅱ)需要分类讨论,然后求出解集即可.
【解答】解:(Ⅰ)由题得a<0且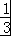 ,
,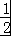 是方程ax2+5x+c=0的两个实数根
是方程ax2+5x+c=0的两个实数根
则 =﹣
=﹣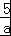 ,
,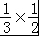 =
= ,解得a=﹣6,c=﹣1,
,解得a=﹣6,c=﹣1,
(Ⅱ)由a=﹣6,c=﹣1,原不等式化为﹣x2+(6+b)x﹣b≥0,
即(6x﹣b)(x﹣1)≤0.
①当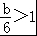 即b>6时,原不等式的解集为[1,
即b>6时,原不等式的解集为[1,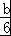 ];
];
②当 =1即b=6时,原不等式的解集为{1};
=1即b=6时,原不等式的解集为{1};
③当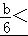 1即b<6时,原不等式的解集为[
1即b<6时,原不等式的解集为[ ,1];
,1];
综上所述:当即b>6时,原不等式的解集为[1, ];
];
当b=6时,原不等式的解集为{1};
当b<6时,原不等式的解集为[ ,1];
,1];
【点评】本题主要考查了不等式的解法,属于基础题.
已知三角形ABC中,A为锐角,且 b=2asinB
b=2asinB
(1)求A,
(2)若a=7,三角形ABC的面积为10 ,求b+c的值.
,求b+c的值.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;正弦定理.
【专题】计算题;转化思想;分析法;解三角形.
【分析】﹙1﹚由正弦定理化简已知结合sinB≠0,可得sinA=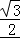 且A为锐角,即可解得A的值.
且A为锐角,即可解得A的值.
(2)利用三角形面积公式解得:bc=40,由余弦定理即可求得b+c的值.
【解答】解:﹙1﹚由正弦定理知a=2RsinA,b=2RsinB,
∴ ×2RsinB=2×2RsinAsinB,sinB≠0,
×2RsinB=2×2RsinAsinB,sinB≠0,
∴sinA=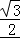 且A为锐角,
且A为锐角,
∴A=60°
(2)∵S=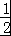 bcsinA=
bcsinA=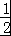 bc×
bc×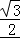 =10
=10 ,
,
∴即解得:bc=40,
∴由余弦定理可求得:49=b2+c2﹣2bccosA=(b+c)2﹣3bc=(b+c)2﹣120,
∴b+c=13.
【点评】本题主要考查了正弦定理,余弦定理,三角形面积公式的综合应用,属于基本知识的考查.
某造纸厂拟建一座平面图形为矩形且面积为162 平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400 元/米,中间两道隔墙建造单价为248 元/米,池底建造单价为80 元/米2,水池所有墙的厚度忽略不计.
(1 )试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2 )若由于地形限制,该池的长和宽都不能超过16 米,试设计污水池的长和宽,使总造价最低.

知识点:14.函数的应用问题
【考点】函数模型的选择与应用.
【专题】应用题;函数思想;数学模型法;函数的性质及应用.
【分析】(1)污水处理池的底面积一定,设宽为x米,可表示出长,从而得出总造价f(x),利用基本不等式求出最小值;
(2)由长和宽的限制条件,得自变量x的范围,判断总造价函数f(x)在x的取值范围内的函数值变化情况,求得最小值.
【解答】解:(1)设污水处理池的宽为x米,则长为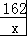 米.
米.
则总造价f(x)=400×(2x+2×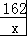 )+248×2x+80×162=1296x+
)+248×2x+80×162=1296x+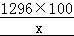 +12960
+12960
=1296(x+ )+12960≥1296×2×
)+12960≥1296×2×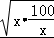 +12960=38880(元),
+12960=38880(元),
当且仅当x= (x>0),即x=10时取等号.
(x>0),即x=10时取等号.
∴当长为16.2 米,宽为10 米时总造价最低,最低总造价为38 880 元.
(2)由限制条件知 ,∴10
,∴10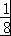 ≤x≤16
≤x≤16
设g(x)=x+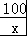 (10
(10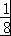 ≤x≤16).g(x)在[10
≤x≤16).g(x)在[10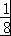 ,16]上是减函数,
,16]上是减函数,
∴当x=16时,g(x)有最小值,即f(x)有最小值.
∴当长为16 米,宽为10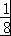 米时,总造价最低.
米时,总造价最低.
【点评】本题考查了建立函数解析式,利用基本不等式求函数最值的能力,还考查了函数的单调性和运算能力.
三角形ABC中,a(cosB+cosC)=b+c,
(1)求证A=
(2)若三角形ABC的外接圆半径为1,求三角形ABC周长的取值范围.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;正弦定理.
【专题】计算题;转化思想;分析法;解三角形.
【分析】(1)由余弦定理化简已知整理可得:(b+c)(a2﹣b2﹣c2)=0,由b+c>0,可得a2=b2+c2,即可解得A=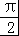 .
.
(2)利用正弦定理可得a=2,b+c=2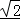 sin(B+
sin(B+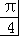 ),结合范围0
),结合范围0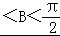 ,可得2<b+c
,可得2<b+c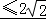 ,从而可求三角形ABC周长的取值范围.
,从而可求三角形ABC周长的取值范围.
【解答】解:(1)证明:∵a(cosB+cosC)=b+c,
∴由余弦定理可得:a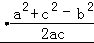 +a
+a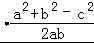 =b+c,
=b+c,
∴整理可得:(b+c)(a2﹣b2﹣c2)=0,
∵b+c>0,
∴a2=b2+c2,
∴A=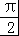 ,得证.
,得证.
(2)∵三角形ABC的外接圆半径为1,A=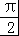 ,
,
∴a=2,
∴b+c=2(sinB+cosB)=2 sin(B+
sin(B+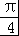 ),
),
∵0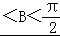 ,
,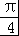 <B+
<B+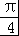 <
<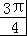 ,
,
∴2<b+c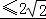 ,
,
∴4<a+b+c≤2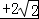 ,
,
∴三角形ABC周长的取值范围是:(4,2+2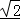 ].
].
【点评】本题主要考查了三角函数恒等变换的应用,考查了正弦定理,余弦定理,勾股定理,正弦函数的图象和性质,属于基本知识的考查.
设数列{an}的前n项的和Sn= an﹣
an﹣ ×2n+1+
×2n+1+ (n=1,2,3,…)
(n=1,2,3,…)
(Ⅰ)求首项a1
(Ⅱ)证明数列{an+2n}是等比数列并求an.
知识点:4.等比数列及其性质
【考点】数列的求和;数列递推式.
【专题】转化思想;数学模型法;等差数列与等比数列.
【分析】(I)Sn= an﹣
an﹣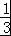 ×2n+1+
×2n+1+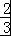 (n=1,2,3,…),当n=1时,a1=S1=
(n=1,2,3,…),当n=1时,a1=S1=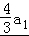 ﹣
﹣ +
+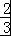 ,解得a1.
,解得a1.
(II)当n≥2时,Sn﹣1=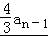 ﹣
﹣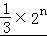 +
+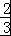 ,化为:an=4an﹣1+2n.变形为
,化为:an=4an﹣1+2n.变形为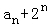 =
=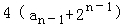 ,即可得出.
,即可得出.
【解答】(I)解:∵Sn=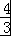 an﹣
an﹣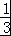 ×2n+1+
×2n+1+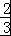 (n=1,2,3,…),
(n=1,2,3,…),
∴当n=1时,a1=S1=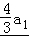 ﹣
﹣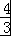 +
+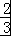 ,解得a1=2.
,解得a1=2.
(II)证明:当n≥2时,Sn﹣1= ﹣
﹣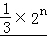 +
+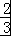 ,
,
可得an=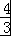 an﹣
an﹣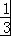 ×2n+1+
×2n+1+ ﹣(
﹣( ﹣
﹣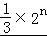 +
+ ),
),
化为:an=4an﹣1+2n.
∴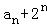 =
=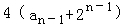 ,
,
∴数列{an+2n}是等比数列,首项为4,公比为4.
∴an+2n=4n,
∴an=4n﹣2n.
【点评】本题考查了递推关系的应用、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.