知识点：2.一元二次不等式及不等式的解法

B

【考点】一元二次不等式的解法．

【专题】不等式的解法及应用．

【分析】把不等式的左边分解因式后，根据两数相乘的取符号法则：同号得正，异号得负，转化为两个一元一次不等式组，求出不等式组的解集即可得到原不等式的解集．

【解答】解：不等式﹣x2+3x+4＜0，

因式分解得：（x﹣4）（x+1）＞0，

可化为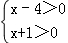：或，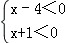

解得：x＞4或x＜﹣1，

则原不等式的解集为{x|x＞4或x＜﹣1}．

故选B．

【点评】本题主要考查了一元二次不等式的解法，考查了转化的数学思想，是一道基础题．

知识点：7.数列的通项

B

【考点】等比数列的通项公式．

【专题】计算题．

【分析】观察此数列是首项是1，且是公比为2的等比数列，根据等比数列的通项公式求出此数列 的一个通项公式．

【解答】解：由于数列1，2，4，8，16，32，…的第一项是1，且是公比为2的等比数列，

故通项公式是 an=1×qn﹣1=2n﹣1，故此数列的一个通项公式an=2n﹣1，

故选B．

【点评】本题主要考查求等比数列的通项公式，求出公比q=2是解题的关键，属于基础题．

知识点：9.正弦定理和余弦定理（解三角形）

A

【考点】正弦定理．

【专题】解三角形．

【分析】先求得A，进而利用正弦定理求得b的值．

【解答】解：A=180°﹣B﹣C=45°，

由正弦定理知=，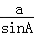

∴b=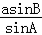==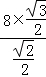4，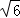

故选A．

【点评】本题主要考查了正弦定理的运用．考查了学生对基础公式的熟练应用．

知识点：1.不等式关系与不等式

C

【考点】不等关系与不等式．

【专题】不等式的解法及应用．

【分析】令a=﹣2，b=﹣1，可得A、B、D都不正确，只有C正确，从而得出结论．

【解答】解：令a=﹣2，b=﹣1，可得A、B、D都不正确，只有C正确，

故选：C．

【点评】本题主要考查不等式的基本性质，利用特殊值代入法，排除不符合条件的选项，是一种简单有效的方法，属于基础题．

知识点：9.正弦定理和余弦定理（解三角形）

B

【考点】等差数列的通项公式；正弦定理．

【专题】计算题；解三角形．

【分析】由题意可得A+C=2B，结合三角形的内角和可求B，进而可求sinB

【解答】解：由题意可得，A+C=2B

∵A+B+C=180°

∴B=60°，sinB=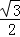

故选B

【点评】本题主要考查了等差数列的性质的简单应用，属于基础试题

知识点：4.等比数列及其性质

A

【考点】等比数列的通项公式．

【专题】计算题．

【分析】设这个等比数列为{an}，根据等比中项的性质可知a2•a4=a1•a5=a23进而求得a3，进而根据a2a3a4=a33，得到答案．

【解答】解：设这个等比数列为{an}，依题意可知a1=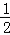，a5=8，则插入的3个数依次为a2，a3，a4，

∴a2•a4=a1•a5=a23=4

∴a3=2

∴a2a3a4=a33=8

故选A．

【点评】本题主要考查了等比数列的性质．主要是利用等比中项的性质来解决．

知识点：5.等比数列的前n项和

A

【考点】等比数列的前n项和．

【专题】等差数列与等比数列．

【分析】利用递推关系及其等比数列的通项公式即可得出．

【解答】解：当n=1时，a1=S1=2+a；

当n≥2时，an=Sn﹣Sn﹣1=2n+a﹣（2n﹣1+a）=2n﹣1，

∵数列{an}为等比数列，

∴a1=2+a=1，解得a=﹣1．

此时an=2n﹣1，a1=1，q=2．

故选：A．

【点评】本题考查了递推关系及其等比数列的通项公式，考查了推理能力与计算能力，属于中档题．

知识点：9.正弦定理和余弦定理（解三角形）

B

【考点】正弦定理．

【专题】解三角形．

【分析】由题意和正余弦定理可得a，c的值，由同角三角函数的基本关系可得sinB，代入三角形的面积公式计算可得．

【解答】解：∵sinC=2sinA，

∴由正弦定理可得c=2a，

又cosB=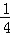，b=2，

由余弦定理可得22=a2+（2a）2﹣2a•2a×，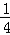

解得a=1，∴c=2，

又cosB=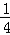，∴sinB==，

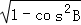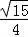∴△ABC的面积S=acsinB=×=

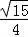
故选：B

【点评】本题考查三角形的面积，涉及正余弦定理的应用，属基础题．

知识点：3.等差数列的前n项和

C

【考点】等差数列的前n项和．

【分析】根据选择项知，要将项的问题转化为前n项和的问题，结合前n项和公式，利用等差数列的性质求得

【解答】解：由等差数列的性质得：a5+a11=2a8

∴a5+a8+a11为定值，即a8为定值

又∵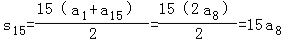

∴s15为定值

故选C

【点评】注意本题中的选择项也是解题信息．

知识点：9.正弦定理和余弦定理（解三角形）

D

【考点】三角形的形状判断．

【专题】解三角形．

【分析】若三角形两边分别为3，4，设第三边为x，则根据三角形三边故选可得：1＜x＜7，由余弦定理可得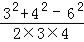＜0，即开判定此三角形为钝角三角形．

【解答】解：若三角形两边分别为3，4，设第三边为x，则根据三角形三边故选可得：1＜x＜7，故可做出这样的三角形．

由余弦定理可得最大边所对的角的余弦值为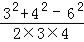：＜0，此三角形为钝角三角形．

故选：D．

【点评】本题主要考查了三角形三边关系余弦定理的应用，属于基础题．

知识点：1.不等式关系与不等式

＞

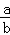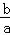
【考点】不等式比较大小．

【专题】不等式的解法及应用．

【分析】利用不等式的基本性质即可得出．

【解答】解：∵a＞b＞0，

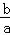∴＜1＜，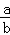

∴＞，

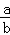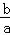故答案为：＞．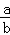

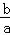【点评】本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．

知识点：9.正弦定理和余弦定理（解三角形）

△ABC为等腰或直角三角形

【考点】正弦定理的应用；两角和与差的余弦函数．

【专题】计算题．

【分析】根据正弦定理把等式acosA=bcosB的边换成角的正弦，再利用倍角公式化简整理得sin2A=sin2B，进而推断A=B，或A+B=90°答案可得．

【解答】解：根据正弦定理可知∵acosA=bcosB，

∴sinAcosA=sinBcosB

∴sin2A=sin2B

∴A=B，或2A+2B=180°即A+B=90°，

所以△ABC为等腰或直角三角形

故答案为△ABC为等腰或直角三角形．

【点评】本题主要考查了正弦定理的应用，属基础题．

知识点：7.数列的通项

n2﹣2n+3

【考点】数列递推式．

【专题】计算题；对应思想；数学模型法；等差数列与等比数列．

【分析】由已知数列递推式，利用累加法求得数列通项公式．

【解答】解：由a1=2，an+1=an+2n﹣1，得

a2﹣a1=2×1﹣1，

a3﹣a2=2×2﹣1，

a4﹣a3=2×3﹣1，

…

an﹣an﹣1=2（n﹣1）﹣1，（n≥2）

累加得：an﹣a1=2﹣（n﹣1），

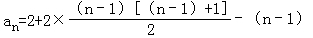∴=n2﹣2n+3（n≥2）．

验证n=1上式成立，

∴an=n2﹣2n+3．

故答案为：n2﹣2n+3．

【点评】本题考查数列递推式，考查了累加法求数列的通项公式，是基础题．

知识点：2.一元二次不等式及不等式的解法

﹣2≤x≤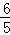

【考点】一元二次不等式的解法．

【专题】不等式的解法及应用．

【分析】设f（x）=（a2﹣4）x2+（a+2）x﹣1，利用二次函数的性质得到二次项系数大于0，根的判别式小于等于0列出关于a的不等式，求出不等式的解集即可确定出a的范围．

【解答】解：设f（x）=（a2﹣4）x2+（a+2）x﹣1，

当a2﹣4=0，即a=﹣2（a=2不是空集）时，不等式解集为空集；

当a2﹣4≠0时，根据题意得：a2﹣4＞0，△≤0，

∴（a+2）2+4（a2﹣4）≤0，即（a+2）（5a﹣6）≤0，

解得：﹣2≤x≤，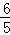

综上a的范围为．

故答案为：

【点评】此题考查了一元二次不等式的解法，以及二次函数的性质，熟练掌握二次函数的性质是解本题的关键．

知识点：5.等比数列的前n项和

510

【考点】等比数列的前n项和．

【专题】等差数列与等比数列．

【分析】易得此人一共走了8次，由等比数列的前n项和公式可得．

【解答】解：∵1+2+3+4+5+6+7+8=36，

∴此人一共走了8次

∵第n次走n米放2n颗石子

∴他投放石子的总数是2+22+23+…+28

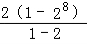==2×255=510

故答案为：510

【点评】本题考查等比数列的求和公式，得出数列的首项和公比是解决问题的关键，属基础题．

知识点：3.等差数列的前n项和

【考点】等比数列的通项公式；等差数列的前n项和．

【专题】计算题．

【分析】（1）设等差数列{an}的公差为d，由已知可得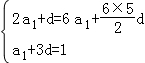，解之即可；（2）由已知可得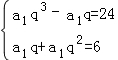，解之可得．

【解答】解：（1）设等差数列{an}的公差为d，

由已知可得，

解之可得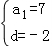，故a5=1+（﹣2）=﹣1；

（2）由已知可得，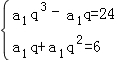

解之可得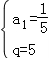

【点评】本题考查等差数列和等比数列的通项公式，属基础题．

知识点：9.正弦定理和余弦定理（解三角形）

【考点】正弦定理；余弦定理．

【专题】解三角形．

【分析】（ I）由正弦定理得，结合二倍角公式及sinA≠0即可得解．

（ II）由（ I）可求sinA，又根据∠B=2∠A，可求cosB，可求sinB，利用三角形内角和定理及两角和的正弦函数公式即可得sinC，利用正弦定理即可得解．

【解答】解：（ I）因为a=3，b=2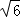，∠B=2∠A．

所以在△ABC中，由正弦定理得．

所以．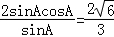

故．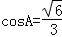

（ II）由（ I）知，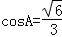

所以．

又因为∠B=2∠A，

所以．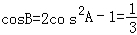

所以．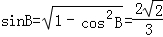

在△ABC中，．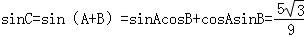

所以．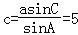

【点评】本题主要考查了正弦定理，同角三角函数关系式，两角和的正弦函数公式的应用，属于基本知识的考查．

知识点：3.等差数列的前n项和

【考点】等差数列的通项公式；数列的函数特性；等差数列的前n项和．

【专题】计算题．

【分析】（1）利用递推公式an=Sn﹣Sn﹣1可求

（2）若使Sn最小，则有an＜0，an+1≥0，求出n的值，代入可求

【解答】解（1）a1=S1=12﹣48×1=﹣47…

当n≥2时 an=Sn﹣Sn﹣1=n2﹣48n﹣=2n﹣49…

a1也适合上式

∴an=2n﹣49（n∈N+）…

（2）a1=﹣47，d=2，所以Sn有最小值

由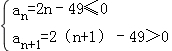

得…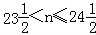

又n∈N+∴n=24即Sn最小…

…

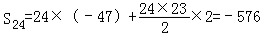或：由Sn=n2﹣48n=（n﹣24）2﹣576∴当n=24时，Sn取得最小值﹣576．

【点评】本题（1）主要考查了利用数列的递推公式an=Sn﹣Sn﹣1求解数列的通项公式，（2）主要考查了求解数列和的最小值问题，主要利用数列的单调性，则满足an＜0，an+1≥0．

知识点：6.数列的求和

【考点】平面向量的基本定理及其意义．

【专题】等差数列与等比数列．

【分析】（1）判断数列{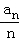}是等差数列，然后求解通项公式．

（2）利用错位相减法求解数列的和即可．

【解答】（本小题12分）

（1）解：由已知可得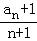﹣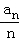=1，…．

所以是以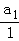=1为首项，1为公差的等差数列．得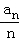=1+（n﹣1）•1=n，

所以an=n2，…

（2）由（1）得an=n2，从而bn=n•3n…．

Sn=1×31+2×32+3×33+…+n•3n①

3Sn=1×32+2×33+3×34+…+（n﹣1）•3n+n•3n+1②

①﹣②得：﹣2Sn=31+32+33+…+3n﹣n•3n+1

=﹣n•3n+1=．…．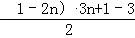

所以Sn=．…．

【点评】本题考查数列的通项公式的应用，数列求和的方法，考查计算能力．

知识点：2.一元二次不等式及不等式的解法

【考点】一元二次不等式的应用；一元二次不等式的解法．

【专题】计算题；分类讨论；函数思想；转化思想；不等式的解法及应用．

【分析】解（x﹣a）（x+a﹣1）=0得：x=a，或x=1﹣a，讨论两个根的大小，结合“小于看中间”可得不等式的解集．

【解答】解：由（x﹣a）（x+a﹣1）=0得：x=a，或x=1﹣a，

当0≤a＜时，＜1﹣a≤1，

解不等式（x﹣a）（x+a﹣1）＜0得：x∈（a，1﹣a），

当a=时，1﹣a=，不等式（x﹣a）（x+a﹣1）＜0解集为∅，

当＜a≤1，时，0≤1﹣a＜

解不等式（x﹣a）（x+a﹣1）＜0得：x∈（1﹣a，a）．

综上：当0≤a＜时，不等式的解集：x∈（a，1﹣a），

当a=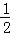时，不等式解集为∅，

当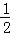＜a≤1时，不等式的解集：x∈（1﹣a，a）．

【点评】本题考查的知识点是二次不等式的解法，分类讨论思想，难度中档．

知识点：14.函数的应用问题

【考点】根据实际问题选择函数类型；基本不等式在最值问题中的应用；数列的应用．

【专题】计算题；应用题．

【分析】（I）由已知中某种汽车购买时费用为14.4万元，每年应交付保险费、养路费及汽油费共0.9万元，汽车的维修费为：第一年0.2万元，第二年0.4万元，第三年0.6万元，…，依等差数列逐年递增，根据等差数列前n项和公式，即可得到f（n）的表达式；

（II）由（I）中使用n年该车的总费用，我们可以得到n年平均费用表达式，根据基本不等式，我们易计算出平均费用最小时的n值，进而得到结论．

【解答】解：（Ⅰ）依题意f（n）=14.4+（0.2+0.4+0.6+…+0.2n）+0.9n …

=…

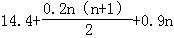=0.1n2+n+14.4…

（Ⅱ）设该车的年平均费用为S万元，则有…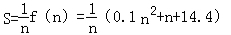

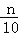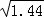=++1≥2+1

=2×1.2+1=3.4

仅当，即n=12时，等号成立．…（13分）

故：汽车使用12年报废为宜．…（14分）

【点评】本题考查的知识点是根据实际问题选择函数类型，基本不等式在最值问题中的应用，数列的应用，其中（I）的关键是由等差数列前n项和公式，得到f（n）的表达式，（II）的关键是根据基本不等式，得到函数的最小值点．