等比数列{an}中,首项a1=8,公比 ,那么{an}前5项和S5的值是( )
,那么{an}前5项和S5的值是( )
A. B.
B. C.
C. D.
D.
知识点:5.等比数列的前n项和
A
考点:等比数列的前n项和.
专题:计算题;等差数列与等比数列.
分析:等比数列{an}中,由首项a1=8,公比 ,利用等比数列的求和公式能求出{an}前5项和S5的值.
,利用等比数列的求和公式能求出{an}前5项和S5的值.
解答:解:等比数列{an}中,
∵首项a1=8,公比 ,
,
∴S5=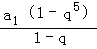 =
=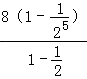 =
= .
.
故选A.
点评:本题考查等比数列的前n项和公式的应用,是基础题.解题时要认真审题,仔细解答
已知等比数列{an}满足:a2=2,a5= ,则公比q为( )
,则公比q为( )
A.﹣ B.
B. C.﹣2 D.2
C.﹣2 D.2
知识点:4.等比数列及其性质
B
考点:等比数列的通项公式.
专题:等差数列与等比数列.
分析:利用等比数列通项公式求解.
解答:解:∵等比数列{an}满足:a2=2,a5=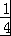 ,
,
∴2q3=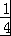 ,
,
解得q=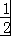 .
.
故选:B.
点评:本题考查等比数列的公比的求法,是基础题,解题时要认真审题,注意等比数列的通项公式的求法
若a>b,则下列命题成立的是( )
A.ac>bc B. >1 C.
>1 C. D.ac2≥bc2
D.ac2≥bc2
知识点:1.不等式关系与不等式
D
考点:不等式的基本性质.
专题:计算题.
分析:通过给变量取特殊值,举反例可得A、B、C都不正确,对于a>b,由于c2≥0,故有 ac2≥bc2,故D成立.
解答:解:∵a>b,故当c=0时,ac=bc=0,故A不成立.
当b=0 时,显然B、C不成立.
对于a>b,由于c2≥0,故有 ac2≥bc2,故D成立.
故选D.
点评:本题主要考查不等式与不等关系,不等式性质的应用,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.
已知正数x,y满足x+2y=1,则 的最小值为( )
的最小值为( )
A.6 B.5 C. D.
D.
知识点:4.基本不等式
C
考点:基本不等式.
专题:计算题.
分析:将原式子变形为 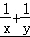 =
=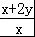 +
+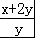 =1+
=1+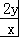 +
+ +2,使用基本不等式,求得最小值.
+2,使用基本不等式,求得最小值.
解答:解:∵正数x,y满足x+2y=1,∴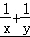 =
=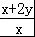 +
+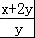 =1+
=1+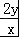 +
+ +2
+2
≥3+2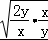 =3+2
=3+2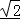 ,当且仅当
,当且仅当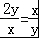 时,等号成立,
时,等号成立,
故选C.
点评:本题考查基本不等式的应用,变形是解题的关键和难点
已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是( )
A.(3,8) B.(4,7) C.(4,8) D.(5,7)
知识点:1.合情推理与演绎推理
D
考点:归纳推理.
专题:计算题;规律型;推理和证明.
分析:根据括号内的两个数的和的变化情况找出规律,然后找出第60对数的两个数的和的值以及是这个和值的第几组,然后写出即可.
解答:解:(1,1),两数的和为2,共1个,
(1,2),(2,1),两数的和为3,共2个,
(1,3),(2,2),(3,1),两数的和为4,共3个,
(1,4),(2,3),(3,2),(4,1),两数的和为5,共4个
…
∵1+2+3+4+5+6+7+8+9+10=55,
∴第60个数对在第11组之中的第5个数,从而两数之和为12,应为(5,7).
故选D.
点评:本题是对数字变化规律的考查,规律比较隐蔽,观察出括号内的两个数的和的变化情况是解题的关键.
等差数列{an}的前n项和为Sn,若Sn=30,S2n=100,则S3n=( )
A.130 B.170 C.210 D.260
知识点:3.等差数列的前n项和
C
考点:等差数列的性质.
专题:计算题.
分析:由等差数列性质可得:sn,s2n﹣sn,s3n﹣s2n…为等差数列,进而结合题中的条件可得答案.
解答:解:因为数列{an}为等差数列,
所以由等差数列性质可得:sn,s2n﹣sn,s3n﹣s2n…为等差数列.
即30,100﹣30,S3n﹣100是等差数列,
∴2×70=30+S3n﹣100,解得S3n=210,
故选C.
点评:解决此类问题的关键是熟练掌握等差数列的性质,利用了等差数列每连续的n 项的和也成等差数列,属于中档题
下列四个结论:
①若x>0,则x>sinx恒成立;
②命题“若x﹣sinx=0,则x=0”的逆命题为“若x≠0,则x﹣sinx≠0”;
③P命题的否命题和P命题的逆命题同真同假④若|C|>0则C>0
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4
知识点:4.命题及其关系
B
考点:命题的真假判断与应用.
专题:综合题;转化思想;综合法;简易逻辑.
分析:令f(x)=x﹣sinx,利用导数分析其单调性,可判断①;写出原命题的逆命题,可判断②;P命题的否命题和P命题的逆命题是等价命题,同真同假,可判断③;若|C|>0则C>0或C<0,可判断④.
解答:解:令f(x)=x﹣sinx,则f′(x)=1﹣cosx≥0恒成立,
故f(x)=x﹣sinx在R上为增函数,故x>0时,f(x)>f(0)=0,
即x>sinx恒成立,故①正确;
命题“若x﹣sinx=0,则x=0”的逆命题为“若x=0,则x﹣sinx=0”,故②错误;
P命题的否命题和P命题的逆命题是等价命题,同真同假,正确;
④若|C|>0则C>0或C<0,不正确.
故选:B.
点评:本题考查函数的单调性的运用,考查逆命题,考查四种命题,属于基础题和易错题.
设等差数列{an}的前n项和为Sn,若a1=﹣11,a4+a6=﹣6,则当Sn取最小值时,n等于( )
A.6 B.7 C.8 D.9
知识点:3.等差数列的前n项和
A
考点:等差数列的前n项和.
专题:等差数列与等比数列.
分析:条件已提供了首项,故用“a1,d”法,再转化为关于n的二次函数解得.
解答:解:设该数列的公差为d,则a4+a6=2a1+8d=2×(﹣11)+8d=﹣6,解得d=2,
所以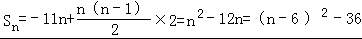 ,所以当n=6时,Sn取最小值.
,所以当n=6时,Sn取最小值.
故选A.
点评:本题考查等差数列的通项公式以及前n项和公式的应用,考查二次函数最值的求法及计算能力
设a>0,b>0若 是3a与3b的等比中项,则
是3a与3b的等比中项,则 的最小值为( )
的最小值为( )
A.  B.
B. C.4 D.
C.4 D.
知识点:4.等比数列及其性质
B
考点:等比数列的通项公式;基本不等式.
专题:转化思想;等差数列与等比数列;不等式.
分析:利用等比数列的性质可得a+b=5.再利用基本不等式的性质即可得出.
解答:解:∵a>0,b>0,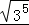 是3a与3b的等比中项,
是3a与3b的等比中项,
∴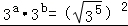 =35,
=35,
化为a+b=5.
则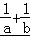 =
=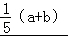
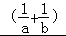 =
=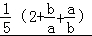
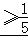
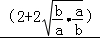 =
=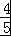 ,当且仅当a=b=
,当且仅当a=b= 时取等号.
时取等号.
故选:B.
点评:本题考查了等比数列的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.
若a>b>0,c<d<0,则一定有( )
A. >
> B.
B. <
< C.
C. >
> D.
D. <
<
知识点:1.不等式关系与不等式
B
考点:不等关系与不等式.
专题:不等式的解法及应用.
分析:利用特例法,判断选项即可.
解答:解:不妨令a=3,b=1,c=﹣3,d=﹣1,
则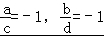 ,
,
∴C、D不正确;
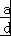 =﹣3,
=﹣3, =﹣
=﹣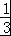
∴A不正确,B正确.
解法二:
∵c<d<0,
∴﹣c>﹣d>0,
∵a>b>0,
∴﹣ac>﹣bd,
∴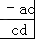
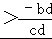 ,
,
∴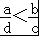 .
.
故选:B.
点评:本题考查不等式比较大小,特值法有效,带数计算正确即可
已知等差数列{an}的前n项和为Sn,若a4=18﹣a5,则S8=( )
A.18 B.36 C.54 D.72
知识点:3.等差数列的前n项和
D
考点:等差数列的前n项和.
专题:等差数列与等比数列.
分析:由等差数列的性质可得a1+a8=a4+a5=18,代入求和公式可得.
解答:解:由题意可得a4+a5=18,
由等差数列的性质可得a1+a8=a4+a5=18,
∴S8= =
=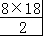 =72
=72
故选:D
点评:本题考查等差数列的性质和求和公式,属基础题
已知数列{an}中,a1=1,an=3an﹣1+4(n∈N*且n≥2),,则数列{an}通项公式an为( )
A.3n﹣1 B.3n+1﹣8 C.3n﹣2 D.3n
知识点:7.数列的通项
C
考点:数列递推式.
专题:计算题.
分析:在an=3an﹣1+4两边同时加上2,整理判断出数列{ an+2}是等比数列,求出{ an+2}的通项后,再求an.
解答:解:在an=3an﹣1+4两边同时加上2,得an+2=3an﹣1+6=3(an﹣1+2),
根据等比数列的定义,数列{ an+2}是等比数列,
且公比为3.以a1+2=3为首项.
等比数列{ an+2}的通项an+2=3•3 n﹣1=3 n,
移向得an=3n﹣2.
故选C.
点评:本题考查等差数列、等比数列的判定,数列通项求解,考查变形构造,转化、计算能力.形如:an+1=pan+q递推数列,这种类型可转化为an+1+m=4(an+m)构造等比数列求解
已知数列{an}的前n项和Sn=n2(n∈N*),则a8的值是__________.
知识点:3.等差数列的前n项和
15
考点:等差数列的性质.
专题:等差数列与等比数列.
分析:利用a8=S8﹣S7,可得结论.
解答:解:∵数列{an}的前n项和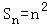 ,
,
∴a8=S8﹣S7=64﹣49=15.
故答案为:15.
点评:本题考查数列的通项与求和,考查学生的计算能力,属于基础题.
已知等比数列{an}的公比q为正数,且 ,则q=__________.
,则q=__________.
知识点:4.等比数列及其性质
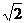
考点:等比数列的通项公式.
专题:等差数列与等比数列.
分析:设出等比数列的首项,由等比数列的通项公式写出a3,a9,a5,代入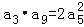 后可直接求得q的值.
后可直接求得q的值.
解答:解:设等比数列的首项为a1,
由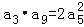 ,得:
,得: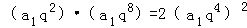 ,
,
即 ,
,
∵a1≠0,q>0,∴q=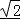 .
.
故答案为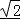 .
.
点评:本题考查了等比数列的通项公式,解答时注意等比数列中不含有为0的项,是基础的计算题
已知实数x,y满足约束条 则
则 的最大值等于_________.
的最大值等于_________.
知识点:3.二元一次不等式(组)与简单的线性规划
8
考点:简单线性规划.
专题:数形结合.
分析:先根据约束条件画出可行域,欲求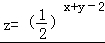 的最大值,即要求z1=x+y﹣2的最小值,再利用几何意义求最值,分析可得z1=x+y﹣2表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最小值即可.
的最大值,即要求z1=x+y﹣2的最小值,再利用几何意义求最值,分析可得z1=x+y﹣2表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最小值即可.
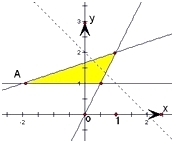
解答:解:作图
易知可行域为一个三角形,
验证知在点A(﹣2,1)时,
z1=x+y﹣2取得最小值﹣3,
∴z最大是8,
故答案为:8.
点评:本题考查线性规划问题,难度较小.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解
不等式 的解集是
__________.
的解集是
__________.
知识点:2.一元二次不等式及不等式的解法
{x|﹣1<x<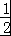 ,x∈R}
,x∈R}
考点:其他不等式的解法.
专题:计算题;转化思想.
分析:不等式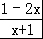 >0说明:1﹣2x 和 x+1是同号的,可等价于(1﹣2x)(x+1)>0,然后解二次不等式即可.
>0说明:1﹣2x 和 x+1是同号的,可等价于(1﹣2x)(x+1)>0,然后解二次不等式即可.
解答:解:不等式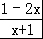 >0等价于(1﹣2x)(x+1)>0,不等式对应方程(1﹣2x)(x+1)=0的两个根是x=﹣1 和 x=
>0等价于(1﹣2x)(x+1)>0,不等式对应方程(1﹣2x)(x+1)=0的两个根是x=﹣1 和 x=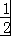 .
.
由于方程对应的不等式是开口向下的抛物线,所以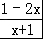 >0的解集为{x|﹣1<x<
>0的解集为{x|﹣1<x<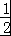 }
}
故答案为:{x|﹣1<x<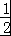 ,x∈R}
,x∈R}
点评:本题考查分式不等式的解法,考查转化思想,计算能力,是基础题.
等比数列{an}中,S2=7,S6=91,求S4.
知识点:5.等比数列的前n项和
28
考点:等比数列的前n项和;等比数列的性质.
专题:计算题.
分析:由等比数列的性质,知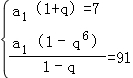 ,从而求出q2=3,再用等比数列的求和公式进行运算就行.
,从而求出q2=3,再用等比数列的求和公式进行运算就行.
解答:解:∵S2=7,S6=91,易知q≠1,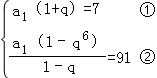
∴由②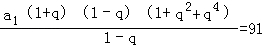 ③
③
∴将①代入③整理得q4+q2﹣12=0,即(q2﹣3)(q2+4)=0
∴q2=3,
∴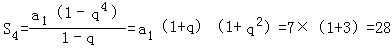 .
.
点评:本题考查数列的性质,解题时要根据等比数列的性质注意公式的灵活运用.
若不等式x2﹣ax﹣b<0的解集为是(2,3),
(1)求a,b的值
(2)求不等式bx2﹣ax﹣1>0的解集.
知识点:2.一元二次不等式及不等式的解法
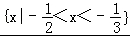
考点:一元二次不等式的解法.
专题:不等式的解法及应用.
分析:(1)根据韦达定理即可求出a,b的值;
(2)由(1)的结论,代入,然后解不等式即可.
解答:解:(1)由已知可知不等式x2﹣ax﹣b<0的解集是{x|2<x<3},
所以2和3是方程x2﹣ax﹣b=0的两个根,
由韦达定理得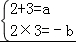 ,
,
解得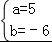 ;
;
(2)不等式bx2﹣ax﹣1>0即为﹣6x2﹣5x﹣1>0,
不等式﹣6x2﹣5x﹣1>0可化为6x2+5x+1<0,
∴(2x+1)(3x+1)<0
解得 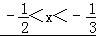 ,
,
所以所求不等式的解集是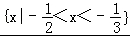 ,
,
点评:本题考查了解一元二次不等式的方法,属于基础题
已知公比为q的等比数列{an}(n∈N*)中,a2=2,前三项的和为7.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若0<q<1,设数列{bn}满足bn=a1•a2…an,n∈N*,求使0<bn<1的n的最小值.
知识点:4.等比数列及其性质
解:(Ⅰ)由已知得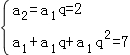 ,
,
解得a1=1且q=2,或a1=4且q= ,
,
∴数列{an}的通项公式为an=2n﹣1或an=( )n﹣3;
)n﹣3;
(Ⅱ)∵0<q<1,∴an=( )n﹣3;
)n﹣3;
∴bn=a1•a2…•an=( )﹣2﹣1+0+…+n﹣3=
)﹣2﹣1+0+…+n﹣3=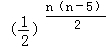 ;
;
由0<bn<1,即0<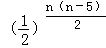 <1,
<1,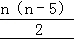 >0,
>0,
解得n>5,∴使0<bn<1的n的最小值为
考点:等比数列的性质.
专题:等差数列与等比数列.
分析:(Ⅰ)由已知可得a1和q的方程组,解方程组代入通项公式可得;
(Ⅱ)由题意易得an=(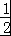 )n﹣3,可得bn=
)n﹣3,可得bn=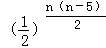 ,由题意可得n的不等式,解不等式可得.
,由题意可得n的不等式,解不等式可得.
解答:解:(Ⅰ)由已知得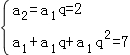 ,
,
解得a1=1且q=2,或a1=4且q= ,
,
∴数列{an}的通项公式为an=2n﹣1或an=( )n﹣3;
)n﹣3;
(Ⅱ)∵0<q<1,∴an=( )n﹣3;
)n﹣3;
∴bn=a1•a2…•an=( )﹣2﹣1+0+…+n﹣3=
)﹣2﹣1+0+…+n﹣3=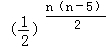 ;
;
由0<bn<1,即0<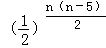 <1,
<1,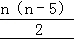 >0,
>0,
解得n>5,∴使0<bn<1的n的最小值为6
点评:本题考查等比数列的性质,涉及等比数列的通项公式和求和公式,属中档题
等比数列{an}的前n项和为Sn,已知S2,S4,S3成等差数列.
(1)求数列{an}的公比q;
(2)若a1﹣a3=3,问 是数列{an}的前多少项和.
是数列{an}的前多少项和.
知识点:2.等差数列及其性质
解:(1)∵S2,S4,S3成等差数列,
∴2S4=S2+S3,
当q=1时,8a1≠2a1+3a1,舍去.
当q≠1时,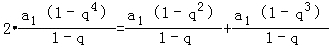 ,
,
整理,得2q2﹣q﹣1=0,解得q=1(舍),或q=﹣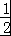 ,
,
∴数列{an}的公比q=﹣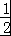 .
.
(2)∵a1﹣a3=3,∴ =3,解得a1=4,
=3,解得a1=4,
∴Sn=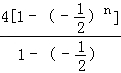 =
=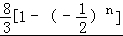 ,
,
∵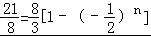 ,解得n=6,
,解得n=6,
∴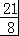 是数列{an}的前6项和.
是数列{an}的前6项和.
考点:数列的求和.
专题:等差数列与等比数列.
分析:(1)由题意知2S4=S2+S3,当q=1时,8a1≠2a1+3a1,舍去.当q≠1时,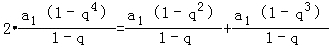 ,由此能求出数列{an}的公比.
,由此能求出数列{an}的公比.
(2)由a1﹣a3=3,解得a1=4,所以Sn=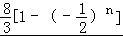 ,由此能求出
,由此能求出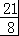 是数列{an}的前6项和.
是数列{an}的前6项和.
解答:解:(1)∵S2,S4,S3成等差数列,
∴2S4=S2+S3,
当q=1时,8a1≠2a1+3a1,舍去.
当q≠1时,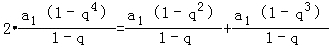 ,
,
整理,得2q2﹣q﹣1=0,解得q=1(舍),或q=﹣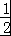 ,
,
∴数列{an}的公比q=﹣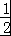 .
.
(2)∵a1﹣a3=3,∴ =3,解得a1=4,
=3,解得a1=4,
∴Sn=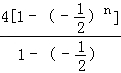 =
=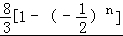 ,
,
∵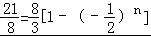 ,解得n=6,
,解得n=6,
∴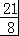 是数列{an}的前6项和.
是数列{an}的前6项和.
点评:本题考查等比数列的公比的求法,考查一个数是等比数列的前几项和的判断,是中档题,解题时要认真审题,注意等比数列的性质的灵活运用
解关于x的不等式x2﹣(2+a)x+2a<0.
知识点:2.一元二次不等式及不等式的解法
解:不等式x2﹣(2+a)x+2a<0可化为
(x﹣2)(x﹣a)<0,
所以,当a=2时,不等式为(x﹣2)2<0,解集为∅;
当a>2时,不等式的解集为{x|2<x<a},
当a<2时,不等式的解集为{x|a<x<2}
考点:一元二次不等式的解法.
专题:分类讨论;不等式的解法及应用.
分析:把不等式化为(x﹣2)(x﹣a)<0,讨论a的取值范围,求出不等式的解集即可.
解答:解:不等式x2﹣(2+a)x+2a<0可化为
(x﹣2)(x﹣a)<0,
所以,当a=2时,不等式为(x﹣2)2<0,解集为∅;
当a>2时,不等式的解集为{x|2<x<a},
当a<2时,不等式的解集为{x|a<x<2}.
点评:本题考查了利用分类讨论思想解含有字母系数的不等式的解法与应用问题,是基础题目.
已知数列{an}满足a1=2,an+1=4an+2n+1(n∈N*).
(1)令bn= ,求证:数列{bn}为等比数列;
,求证:数列{bn}为等比数列;
(2)求数列{an}的通项公式;
(3)求满足an≥240的最小正整数n.
知识点:4.等比数列及其性质
证明:(1)∵an+1=4an+2n+1,bn=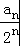 +1,
+1,
∴bn+1=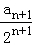 +1=
+1=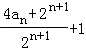 =
=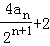 =2(
=2(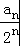 +1)=2bn,
+1)=2bn,
又∵a1=2,
∴b1=2,
∴数列{bn}是首项为2,公比为2的等比数列,
(2)由(1)得:bn=2n,
即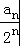 +1=2n,
+1=2n,
∴an=4n﹣2n,
(3)令t=2n,则an≥240可化为:
t2﹣t≥240,
解得:t≥16,
即2n≥16,n≥4,
故满足an≥240的最小正整数n=4
考点:数列递推式;等比关系的确定.
专题:等差数列与等比数列.
分析:(1)由an+1=4an+2n+1,bn=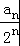 +1,可得bn+1=2bn,结合a1=2,可得数列{bn}是首项为2,公比为2的等比数列,
+1,可得bn+1=2bn,结合a1=2,可得数列{bn}是首项为2,公比为2的等比数列,
(2)由(1)得:bn=2n,结合bn=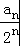 +1,可得数列{an}的通项公式;
+1,可得数列{an}的通项公式;
(3)令t=2n,则an≥240可化为:t2﹣t≥240,先解二次不等式,再解指数不等式可得答案.
解答:证明:(1)∵an+1=4an+2n+1,bn=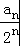 +1,
+1,
∴bn+1=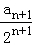 +1=
+1=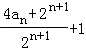 =
=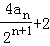 =2(
=2(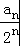 +1)=2bn,
+1)=2bn,
又∵a1=2,
∴b1=2,
∴数列{bn}是首项为2,公比为2的等比数列,
(2)由(1)得:bn=2n,
即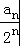 +1=2n,
+1=2n,
∴an=4n﹣2n,
(3)令t=2n,则an≥240可化为:
t2﹣t≥240,
解得:t≥16,
即2n≥16,n≥4,
故满足an≥240的最小正整数n=4
点评:本题考查的知识点是数列的递推公式,数列的通项公式,等比数列的证明,解指数不等式,二次不等式,是数列与不等式的综合应用,难度中档