复数 (i为虚数单位)的虚部是( )
(i为虚数单位)的虚部是( )
A. B.
B. C.
C. D.
D.
知识点:3.复数代数形式的四则运算
B
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数的运算法则、虚部的定义即可得出.
【解答】解:复数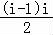 =﹣
=﹣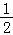 ﹣
﹣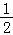 i,虚部为﹣
i,虚部为﹣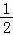 .
.
故选:B.
【点评】本题考查了复数的运算法则、虚部的定义,考查了推理能力与计算能力,属于基础题.
在用反证法证明命题“过一点只有一条直线与已知平面垂直”时,应假设( )
A.过两点有一条直线与已知平面垂直
B.过一点有一条直线与已知平面平行
C.过一点有两条直线与已知平面垂直
D.过一点有一条直线与已知平面不垂直
知识点:2.直接证明与间接证明
C
【考点】R9:反证法与放缩法.
【分析】假设的结论为原结论的否定.
【解答】解:命题“过一点只有一条直线与已知平面垂直”的否定为:过一点至少有两条直线与已知平面垂直,
故选C.
【点评】本题考查了反证法证明,属于基础题.
函数f(x)=2x3在点(﹣1,f(﹣1))处的切线方程为( )
A.y=6x+4 B.y=6x﹣4 C.y=﹣6x+4 D.y=﹣6x﹣4
知识点:1.变化率与导数
A
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】求出函数的导函数,得到f′(﹣1),再求出f(﹣1),利用直线方程的点斜式得答案.
【解答】解:由f(x)=2x3,得f′(x)=6x2,
∴f′(﹣1)=6.
又f(﹣1)=﹣2,
∴点(﹣1,f(﹣1))为(﹣1,﹣2),
则函数f(x)=2x3在点(﹣1,f(﹣1))处的切线方程为y+2=6(x+1),
即y=6x+4.
故选:A.
【点评】本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处得导数值,是中档题.
某数学老师在分析上期末考试成绩时发现:本班的数学成绩(x)与总成绩(y)之间满足线性回归方程: ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.某同学数学成绩好,则总成绩一定也好
B.若该班的数学平均分为110分,则总成绩平均分一定为530分
C.若某同学的数学成绩为110分,则他的总成绩一定为530分
D.本次统计中的相关系数为1.8
知识点:4.回归分析的基本思想及其初步应用
B
【考点】BK:线性回归方程.
【分析】根据两个变量之间线性回归方程的定义与性质,对选项中的命题判断正误即可.
【解答】解:对于A,某同学数学成绩好,根据回归方程预测他的总成绩可能也好,∴A错误;
对于B,根据回归直线过样本中心点,当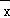 =110时,
=110时,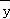 =1.8×110+332=530,∴B正确;
=1.8×110+332=530,∴B正确;
对于C,某同学的数学成绩为110分时,预测他的总成绩可能为530分,∴C正确;
对于D,在线性回归方程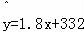 中,相关系数r∈(0,1),不是1.8,∴D错误.
中,相关系数r∈(0,1),不是1.8,∴D错误.
故选:B.
【点评】本题考查了线性回归方程的定义与应用问题,是基础题.
在下列图、表中,能更直观地反映两个分类变量是否有关系的是( )
A.列联表 B.散点图 C.残差图 D.等高条形图
知识点:3.变量间的相关关系
D
【考点】BN:独立性检验的基本思想.
【分析】根据题意,依次分析选项的图、表,结合其统计意义,即可得答案.
【解答】解:根据题意,分析选项:
对于A、对于列联表,需要计算k2的值,不是直观的分析;
对于B、散点图体现的是变量间相关性的强弱,
对于C、残插图体现预报变量与实际值之间的差距,
对于D、等高条形图能直观地反映两个分类变量是否有关系,
故选:D.
【点评】本题考查分类变量的关系的判定,直观上判定的方法是等高条形图.
执行如图所示的程序框图,若输入n的值为5,则输出s的值是( )

A.4 B.6 C.9 D.13
知识点:1.算法与程序框图
C
【考点】EF:程序框图.
【分析】模拟执行如图所示的程序框图,即可得出程序运行后输出的s值.
【解答】解:执行如图所示的程序框图,如下;
输入n=5,i=2,s=3,i≤n;
s=3+0=3,i=3,i≤n;
s=3+1=4,i=4,i≤n;
s=4+2=6,i=5,i≤n;
s=6+3=9,i=6,i>n;
结束循环,输出s=9.
故选:C.
【点评】本题考查了程序框图的应用问题,是基础题.
函数y=x2﹣2lnx的单调递减区间为( )
A.(﹣1,1) B.(0,1] C.[1,+∞) D.(0,+∞)
知识点:3.导数在研究函数中的应用
B
【考点】6B:利用导数研究函数的单调性.
【分析】求出原函数的导函数,再由导函数小于0求得函数的单调减区间.
【解答】解:由y=x2﹣2lnx,得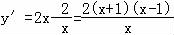 (x>0).
(x>0).
由y′<0,得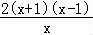 <0,解得x<﹣1或0<x<1.
<0,解得x<﹣1或0<x<1.
∵x>0,
∴函数y=x2﹣2lnx的单调递减区间为(0,1].
故选:B.
【点评】本题考查利用导数研究函数的单调性,考查函数的单调性与导函数符号间的关系,是基础题.
若 ,
, ,(a>﹣5),则P,Q的大小关系为( )
,(a>﹣5),则P,Q的大小关系为( )
A.P<Q B.P=Q C.P>Q D.不能确定
知识点:1.不等式关系与不等式
C
【考点】72:不等式比较大小.
【分析】计算P2,Q2,比较(a+6)(a+7)和(a+5)(a+8)的大小关系,即可得出P2,Q2的大小关系,从而得出P,Q的大小关系.
【解答】解:P2=2a+13+2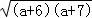 ,Q2=2a+13+2
,Q2=2a+13+2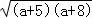 ,
,
∵(a+6)(a+7)﹣(a+5)(a+8)=a2+13a+42﹣(a2+13a+40)=2>0,
∴(a+6)(a+7)>(a+5)(a+8),
∴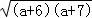 >
>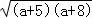 ,
,
∴P2>Q2,
∴P>Q.
故选C.
【点评】本题考查了不等式比较大小,属于基础题.
某产品的销售收入y1(万元)是产量x(千台)的函数: (x>0),生产成本y2万元是产量x(千台)的函数:
(x>0),生产成本y2万元是产量x(千台)的函数: (x>0),为使利润最大,应生产( )
(x>0),为使利润最大,应生产( )
A.9千台 B.8千台 C.7千台 D.6千台
知识点:4.生活中的优化问题举例
D
【考点】3H:函数的最值及其几何意义.
【分析】由题意得到利润关于产量的函数式,再由导数求得使利润最大时的产量.
【解答】解:由题意,利润y=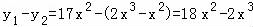 (x>0).
(x>0).
y′=36x﹣6x2,
由y′=36x﹣6x2=6x(6﹣x)=0,得x=6(x>0),
当x∈(0,6)时,y′>0,当x∈(6,+∞)时,y′<0.
∴函数在(0,6)上为增函数,在(6,+∞)上为减函数.
则当x=6(千台)时,y有最大值为144(万元).
故选:D.
【点评】本题考查函数的最值及其几何意义,简单的数学建模思想方法,训练了利用导数求最值,是中档题.
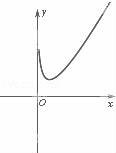
已知函数f(x)=x2+x+2cosx,若f'(x)是f(x)的导函数,则函数f'(x)的图象大致是( )
A. B.
B. C.
C. D.
D.
知识点:3.导数在研究函数中的应用
A
【考点】6A:函数的单调性与导数的关系.
【分析】由题可得f′(x)=2x﹣2sinx+1,判断导函数的奇偶性,利用特殊值的函数值推出结果即可.
【解答】解:函数f(x)=x2+x+2cosx,
∴f′(x)=2x+1﹣2sinx=2(x﹣sinx)+1,
而y=2(x﹣sinx)是奇函数,
故f′(x)的图象是y=2(x﹣sinx)的图象向上平移1个单位,
导函数是奇函数,
∵x∈(0,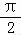 ),x>sinx>0,
),x>sinx>0,
∴B、C、D不正确.
故选:A.
【点评】本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力.
已知函数f(x)=e2x﹣1,直线l过点(0,﹣e)且与曲线y=f(x)相切,则切点的横坐标为( )
A.1 B.﹣1 C.2 D.e﹣1
知识点:1.变化率与导数
A
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】设出切点坐标,求出原函数的导函数,得到曲线在切点处的切线方程,把点(0,﹣e)代入,利用函数零点的判定求得切点横坐标.
【解答】解:由f(x)=e2x﹣1,得f′(x)=2e2x﹣1,
设切点为( ),则f′(x0)=
),则f′(x0)=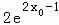 ,
,
∴曲线y=f(x)在切点处的切线方程为y﹣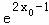 =
=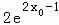 (x﹣x0).
(x﹣x0).
把点(0,﹣e)代入,得﹣e﹣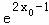 =﹣
=﹣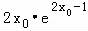 ,
,
即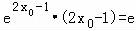 ,两边取对数,得(2x0﹣1)+ln(2x0﹣1)﹣1=0.
,两边取对数,得(2x0﹣1)+ln(2x0﹣1)﹣1=0.
令g(x)=(2x﹣1)+ln(2x﹣1)﹣1,
函数g(x)为(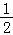 ,+∞)上的增函数,又g(1)=0,
,+∞)上的增函数,又g(1)=0,
∴x=1,即x0=1.
故选:A.
【点评】本题考查利用导数研究过曲线上某点处的切线方程,考查函数零点的判定及应用,是中档题.
已知f(x)为R上的可导函数,且∀x∈R,均有f(x)+f'(x)<0,则以下判断正确的是( )
A.e2017•f(2017)>f(0)
B.e2017•f(2017)=f(0)
C.e2017•f(2017)<f(0)
D.e2017f(2017)与f(0)的大小无法确定
知识点:3.导数在研究函数中的应用
C
【考点】6A:函数的单调性与导数的关系.
【分析】令g(x)=exf(x),求出函数的导数,根据函数的单调性,可得结论.
【解答】解:令g(x)=exf(x),
则g′(x)=ex[f(x)+f′(x)]<0,
故g(x)在R递减,
故g(2017)<g(0),
即e2017f(2017)<f(0),
故选:C.
【点评】本题考查了函数的单调性问题,考查导数的应用,是一道基础题.
《数学万花筒》第3页中提到如下“奇特的规律”:
1×1=1
11×11=121
111×111=12321
…
按照这种模式,第5个式子11111×11111= .
知识点:1.合情推理与演绎推理
123454321
【考点】F1:归纳推理.
【分析】各个数字均为1,当因数为n位时,积的数字为从1排到n,再从n排到1.
【解答】解:根据题意可得111111×111111=123454321,
故答案为:123454321
【点评】本题考查了归纳推理的问题,关键找到规律,属于基础题
《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写的信中提到:“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”回答他这个问题用了124年,但简单的图形我们能用逐一列举的方法解决.若用红、黄、蓝、绿四种颜色给右边的地图着色,假定区域①已着红色,区域②已着黄色,则剩余的区域③④共有 种着色方法.

知识点:1.两个计数原理
2
【考点】D3:计数原理的应用.
【分析】先涂区域③,再涂区域④,使用列举法得出不同的涂色方案.
【解答】解:区域③只能涂蓝色或绿色,
若区域③涂蓝色,则区域④只能涂绿色,
若区域③涂绿色,则区域④只能涂蓝色,
故只有2种涂色方法.
故答案为2.
【点评】本题考查了分步乘法计数原理,属于基础题.
已知i是虚数单位,则 = .
= .
知识点:3.复数代数形式的四则运算
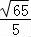
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
【解答】解:∵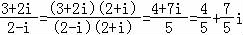 ,
,
∴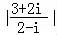 =
=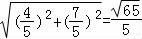 .
.
故答案为: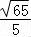 .
.
【点评】本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=ex﹣2ax.若函数f(x)在R内没有零点,则a的取值范围是 .
知识点:13.函数与方程
a<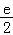
【考点】3L:函数奇偶性的性质.
【分析】作出y=ex与直线y=2ax的函数图象,令两图象在[0,+∞)上无交点得出a的范围.
【解答】解:∵f(x)无零点,且f(x)是偶函数,
∴y=ex与直线y=2ax在[0,+∞)上无交点,
作出y=ex与直线y=2ax的函数图象,如图所示:
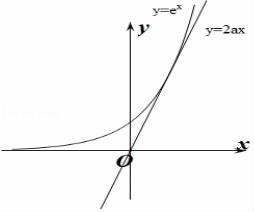
设直线y=2ax与y=ex相切,切点为(m,n),
则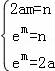 ,解得
,解得 ,
,
∴a<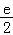 .
.
故答案为: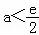 .
.
【点评】本题考查了函数零点与函数图象的关系,属于中档题.
“雷神”火锅为提高销售业绩,委托我校同学研究气温对营业额的影响,并提供了一份该店在3月份中5天的日营业额y(千元)与当日最低气温x(℃)的数据,如表:
x
2
5
8
9
11
y
12
10
8
8
7
(Ⅰ)请你求出y关于x的回归方程 ;
;
(Ⅱ)若4月份某天的最低气温为13摄氏度,请预测该店当日的营业额.
【参考公式】 =
= =
= .
.
知识点:4.回归分析的基本思想及其初步应用
【考点】BK:线性回归方程.
【分析】(Ⅰ)根据表中数据,计算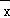 、
、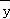 ,
,
求出回归系数,写出回归方程;
(Ⅱ)利用回归方程计算x=13时 的值即可.
的值即可.
【解答】解:(Ⅰ)根据表中数据,计算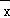 =
=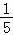 ×(2+5+8+9+11)=7,
×(2+5+8+9+11)=7,
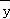 =
= ×(12+10+8+8+7)=9,
×(12+10+8+8+7)=9,
回归系数为
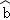 =
=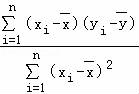 =
=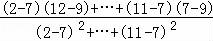 =
=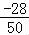 =﹣0.56,
=﹣0.56,
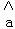 =
=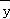 ﹣
﹣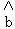
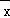 =9﹣(﹣0.56)×7=12.92,
=9﹣(﹣0.56)×7=12.92,
所以,回归方程为: =﹣0.56x+12.92;
=﹣0.56x+12.92;
(Ⅱ)当x=13时, =﹣0.56×13+12.92=5.64,
=﹣0.56×13+12.92=5.64,
当某天的最低气温为13摄氏度,预测该店当日的营业额5.64千元.
【点评】本题考查了线性回归方程的求法与应用问题,是基础题.
年级组长徐老师为教育同学们合理使用手机,在本年级内随机抽取了30名同学做问卷调查.经统计,在这30名同学中长时间使用手机的同学恰占总人数的 ,长时间使用手机且年级名次200名以内的同学有4人,短时间用手机而年级名次在200名以外的同学有2人.
,长时间使用手机且年级名次200名以内的同学有4人,短时间用手机而年级名次在200名以外的同学有2人.
(Ⅰ)请根据已知条件完成2×2列联表;
长时间用手机
短时间用手机
总计
名次200以内
名次200以外
总计
(Ⅱ)判断我们是否有99%的把握认为“学习成绩与使用手机时间有关”
【附表及公式】
P(K2≥k0)
0.010
0.005
0.001
k0
6.635
7.879
10.828
知识点:5.独立性检验的基本思想及其初步运用
【考点】BO:独立性检验的应用.
【分析】(Ⅰ)根据题意,填写列联表即可;
(Ⅱ)根据表中数据,计算观测值,对照临界值得出结论.
【解答】解:(Ⅰ)根据题意,填写列联表如下;
| 长时间用手机 | 短时间用手机 | 总计 |
名次200以内 | 4 | 8 | 12 |
名次200以外 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅱ)根据表中数据,计算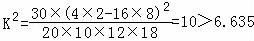 ,
,
对照临界值P(K2≥6.635)=0.01,
所以,有99%的把握认为“学习成绩与使用手机时间有关”.
【点评】本题考查了列联表与独立性检验的应用问题,是基础题.
已知函数 ,其中a∈R
,其中a∈R
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线垂直于直线 ,求a的值;
,求a的值;
(Ⅱ)若f(x)在(0,6)上单调递减,(6,+∞)上单调递增,求a的值.
知识点:3.导数在研究函数中的应用
【考点】6B:利用导数研究函数的单调性;6H:利用导数研究曲线上某点切线方程.
【分析】(Ⅰ)求出函数的导数,计算f′(1),得到关于a的方程,解出即可;(Ⅱ)根据f′(6)=0,得到关于a的方程,解出即可.
【解答】解:(Ⅰ) ,
,
由题设知: ,
,
解得: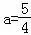 ;
;
(Ⅱ)由题设知,f(x)在x=6处取得极值,
则f'(6)=0,
所以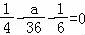 ,
,
解得:a=3.
【点评】本题考查了导数的应用以及函数的单调性问题,是一道基础题.
设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
知识点:3.导数在研究函数中的应用
【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性;6E:利用导数求闭区间上函数的最值.
【分析】(Ⅰ)由f(x)=ex﹣2x+2a,x∈R,知f′(x)=ex﹣2,x∈R.令f′(x)=0,得x=ln2.列表讨论能求出f(x)的单调区间区间及极值.
(Ⅱ)设g(x)=ex﹣x2+2ax﹣1,x∈R,于是g′(x)=ex﹣2x+2a,x∈R.由(1)知当a>ln2﹣1时,g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.由此能够证明ex>x2﹣2ax+1.
【解答】(Ⅰ)解:∵f(x)=ex﹣2x+2a,x∈R,
∴f′(x)=ex﹣2,x∈R.
令f′(x)=0,得x=ln2.
于是当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,ln2) | ln2 | (ln2,+∞) |
f′(x) | ﹣ | 0 | + |
f(x) | 单调递减 | 2(1﹣ln2+a) | 单调递增 |
故f(x)的单调递减区间是(﹣∞,ln2),
单调递增区间是(ln2,+∞),
f(x)在x=ln2处取得极小值,
极小值为f(ln2)=eln2﹣2ln2+2a=2(1﹣ln2+a),无极大值.
(Ⅱ)证明:设g(x)=ex﹣x2+2ax﹣1,x∈R,
于是g′(x)=ex﹣2x+2a,x∈R.
由(1)知当a>ln2﹣1时,
g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.
于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.
于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.
即ex﹣x2+2ax﹣1>0,
故当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
【点评】本题考查函数的单调区间及极值的求法和不等式的证明,具体涉及到导数的性质、函数增减区间的判断、极值的计算和不等式性质的应用.解题时要认真审题,仔细解答.
已知函数f(x)=ax+lnx(a∈R),g(x)=x2﹣2x+2
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若∀x1∈(0,+∞),均∃x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
知识点:3.导数在研究函数中的应用
【考点】6B:利用导数研究函数的单调性;6E:利用导数求闭区间上函数的最值.
【分析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)问题可转化为f(x)max<g(x)max,根据函数的单调性分别求出f(x)的最大值和g(x)的最大值,求出a的范围即可.
【解答】解:(Ⅰ)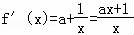 ,
,
①当a≥0时,∵x>0,∴f'(x)>0,
所以f(x)的单调增区间为(0,+∞),
②当a<0时,
令f'(x)>0,得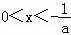 ,
,
令f'(x)<0,得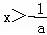 ,
,
所以f(x)的单调增区间为(0,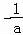 ),
),
单调减区间为(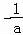 ,+∞);
,+∞);
(Ⅱ)问题可转化为f(x)max<g(x)max,
已知g(x)=(x﹣1)2+1,x∈[0,1],所以g(x)max=2,
由(Ⅰ)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意;
当a<0时,所以f(x)在(0,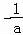 )上单调递增,在(
)上单调递增,在(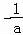 ,+∞)单调递减,
,+∞)单调递减,
故f(x)max=f(﹣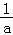 )=﹣1+ln(﹣
)=﹣1+ln(﹣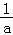 )=﹣1﹣ln(﹣a),
)=﹣1﹣ln(﹣a),
所以2>﹣1﹣ln(﹣a),
解得:a<﹣e﹣3.
【点评】本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.
已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若函数y=f(x)+g(x)有两个不同的极值点x1,x2(x1<x2)且x2﹣x1>ln2,求实数a的取值范围.
知识点:3.导数在研究函数中的应用
【考点】6E:利用导数求闭区间上函数的最值;6D:利用导数研究函数的极值.
【分析】(Ⅰ)求导数,再分类讨论,确定函数在区间上的单调性,即可求得函数的最小值;
(Ⅱ)函数由两个不同的极值点转化为导函数等于0的方程有两个不同的实数根,进而转化为图象的交点问题,由此可得结论.
【解答】解:(Ⅰ)由f′(x)=lnx+1=0,可得x=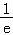 ,
,
∴∴①0<t<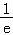 ,时,函数f(x)在(t,
,时,函数f(x)在(t,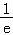 )上单调递减,在(
)上单调递减,在(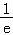 ,t+2)上单调递增,
,t+2)上单调递增,
∴函数f(x)在[t,t+2](t>0)上的最小值为f(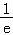 )=﹣
)=﹣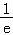 ,
,
②当t≥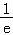 时,f(x)在[t,t+2]上单调递增,
时,f(x)在[t,t+2]上单调递增,
∴f(x)min=f(t)=tlnt,
∴f(x)min=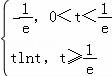 ;
;
(Ⅱ)y=f(x)+g(x)=xlnx﹣x2+ax﹣2,则y′=lnx﹣2x+1+a
题意即为y′=lnx﹣2x+1+a=0有两个不同的实根x1,x2(x1<x2),
即a=﹣lnx+2x﹣1有两个不同的实根x1,x2(x1<x2),
等价于直线y=a与函数G(x)=﹣lnx+2x﹣1的图象有两个不同的交点
∵G′(x)=﹣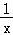 +2,∴G(x)在(0,
+2,∴G(x)在(0,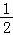 )上单调递减,在(
)上单调递减,在(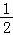 ,+∞)上单调递增,
,+∞)上单调递增,
画出函数图象的大致形状(如右图),
由图象知,当a>G(x)min=G(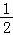 ))=ln2时,x1,x2存在,且x2﹣x1的值随着a的增大而增大而当x2﹣x1=ln2时,由题意
))=ln2时,x1,x2存在,且x2﹣x1的值随着a的增大而增大而当x2﹣x1=ln2时,由题意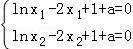 ,
,
两式相减可得ln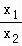 =2(x1﹣x2)=﹣2ln2
=2(x1﹣x2)=﹣2ln2
∴x2=4x1代入上述方程可得x2=4x1=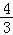 ln2,
ln2,
此时a=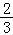 ln2﹣ln(
ln2﹣ln(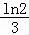 )﹣1,
)﹣1,
所以,实数a的取值范围为a>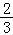 ln2﹣ln(
ln2﹣ln(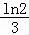 )﹣1;
)﹣1;
【点评】本题考查导数知识的运用,考查函数的单调性与最值,考查的知识点比较多,考查数形结合的数学思想,综合性强.