若复数z满足z(1﹣i)=| +i|,则在复平面内z的共轭复数对应的点位于( )
+i|,则在复平面内z的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
知识点:2.复数的几何意义
D
【考点】复数的代数表示法及其几何意义.
【分析】利用复数的运算法则、几何意义即可得出.
【解答】解:复数z满足z(1﹣i)=| +i|,∴z(1﹣i)(1+i)=2(1+i),
+i|,∴z(1﹣i)(1+i)=2(1+i),
∴z=1+i,
则在复平面内z的共轭复数1﹣i对应的点(1,﹣1)位于第四象限.
故选:D.
已知函数f(x)= x3﹣2ax2﹣3x(a∈R),若函数f(x)的图象上点P(1,m)处的切线方程为3x﹣y+b=0,则m的值为( )
x3﹣2ax2﹣3x(a∈R),若函数f(x)的图象上点P(1,m)处的切线方程为3x﹣y+b=0,则m的值为( )
A.﹣ B.﹣
B.﹣ C.
C. D.
D.
知识点:1.直线的倾斜角、斜率与方程
A
【考点】利用导数研究曲线上某点切线方程.
【分析】求函数的导数,根据导数的几何意义,由已知切线方程建立条件关系,解方程即可得到结论.
【解答】解:∵函数f(x)的图象上点P(1,m)处的切线方程为3x﹣y+b=0,
∴切线斜率k=3,即f′(1)=3,
∵函数f(x)= x3﹣2ax2﹣3x,
x3﹣2ax2﹣3x,
∴f′(x)=2x2﹣4ax﹣3,
则f′(1)=2﹣4a﹣3=3,
解得a=﹣1,
则f(1)= ﹣2a﹣3=
﹣2a﹣3= ﹣2×(﹣1)﹣3=﹣
﹣2×(﹣1)﹣3=﹣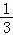 ,
,
即m=﹣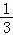 ,
,
故选:A.
用数学归纳法证明命题:1+2+3+…+n2= 时,则从n=k到n=k+1左边需增加的项数为( )
时,则从n=k到n=k+1左边需增加的项数为( )
A.2n﹣1 B.2n C.2n+1 D.n2﹣n+1
知识点:8.数学归纳法
C
【考点】数学归纳法.
【分析】根据等式1+2+3+…+n2=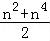 时,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
时,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
【解答】解:当n=k时,等式左端=1+2++k2,
当n=k+1时,等式左端=1+2++k2+(k2+1)+(k2+2)+(k2+3)+…+(k+1)2,
所以增加的项数为:(k+1)2﹣(k2+1)+1=2k+1
即增加了2k+1项.
故选:C
已知点P在曲线y= 上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
A.[0, ) B.[
) B.[ ,
, )C.(
)C.( ,
, ] D.[
] D.[ ,π)
,π)
知识点:1.变化率与导数
D
【考点】导数的几何意义.
【分析】利用导数在切点处的值是曲线的切线斜率,再根据斜率等于倾斜角的正切值求出角的范围.
【解答】解:因为y′=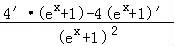 =
=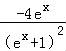 =
= ,
,
∵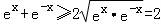 ,
,
∴ex+e﹣x+2≥4,
∴y′∈[﹣1,0)
即tanα∈[﹣1,0),
∵0≤α<π
∴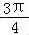 ≤α<π
≤α<π
故选:D.
已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )

A. B.
B. C.
C. D.
D.
知识点:3.导数在研究函数中的应用
A
【考点】利用导数研究函数的单调性.
【分析】观察函数y=f(x)的图象知,f(x)在(0,+∞)上是减函数,f(x)在(﹣∞,0)从左到右,先增再减最后增;从而确定导数的正负,从而求解.
【解答】解:观察函数y=f(x)的图象知,
f(x)在(0,+∞)上是减函数,故y=f′(x)<0在(0,+∞)恒成立,故排除B,D,
f(x)在(﹣∞,0)从左到右,先增再减最后增,故y=f′(x)在(﹣∞,0)从左到右,先“+”再“﹣”最后“+”恒成立,故排除C,
故选:A.
过点(3,1)作圆(x﹣1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为( )
A.2x+y﹣3=0 B.2x﹣y﹣3=0 C.4x﹣y﹣3=0 D.4x+y﹣3=0
知识点:4.直线与圆的位置关系
A
【考点】圆的切线方程;直线的一般式方程.
【分析】由题意判断出切点(1,1)代入选项排除B、D,推出令一个切点判断切线斜率,得到选项即可.
【解答】解:因为过点(3,1)作圆(x﹣1)2+y2=1的两条切线,切点分别为A,B,所以圆的一条切线方程为y=1,切点之一为(1,1),显然B、D选项不过(1,1),B、D不满足题意;另一个切点的坐标在(1,﹣1)的右侧,所以切线的斜率为负,选项C不满足,A满足.
故选A.
已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=( )
A.4 B.8 C.2 D.1
知识点:1.变化率与导数
B
【考点】利用导数研究曲线上某点切线方程.
【分析】求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.
【解答】解:y=x+lnx的导数为y′=1+ ,
,
曲线y=x+lnx在x=1处的切线斜率为k=2,
则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2,即y=2x﹣1.
由于切线与曲线y=ax2+(a+2)x+1相切,
y=ax2+(a+2)x+1可联立y=2x﹣1,
得ax2+ax+2=0,
又a≠0,两线相切有一切点,
所以有△=a2﹣8a=0,
解得a=8.
故选:B.
如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )

A.8π B.6π C.11π D.5π
知识点:11.球
B
【考点】球的体积和表面积.
【分析】把棱锥扩展为正四棱柱,求出正四棱柱的外接球的半径就是三棱锥的外接球的半径,从而可求球的表面积.
【解答】解:由题意可知△A′EF是等腰直角三角形,且A′D⊥平面A′EF.
三棱锥的底面A′EF扩展为边长为1的正方形,
然后扩展为正四棱柱,三棱锥的外接球与正四棱柱的外接球是同一个球,
正四棱柱的对角线的长度就是外接球的直径,直径为: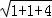 =
=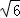 .
.
∴球的半径为 ,
,
∴球的表面积为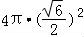 =6π.
=6π.
故选:B.
若点P是曲线y=x2﹣lnx上任意一点,则点P到直线y=x﹣2的最小距离为( )
A. B.1 C.
B.1 C. D.2
D.2
知识点:1.变化率与导数
C
【考点】点到直线的距离公式.
【分析】由题意知,当曲线上过点P的切线和直线y=x﹣2平行时,点P到直线y=x﹣2的距离最小.求出曲线对应的函数的导数,令导数值等于1,可得切点的坐标,此切点到直线y=x﹣2的距离即为所求.
【解答】解:点P是曲线y=x2﹣lnx上任意一点,
当过点P的切线和直线y=x﹣2平行时,
点P到直线y=x﹣2的距离最小.
直线y=x﹣2的斜率等于1,
令y=x2﹣lnx,得 y′=2x﹣ =1,解得x=1,或x=﹣
=1,解得x=1,或x=﹣ (舍去),
(舍去),
故曲线y=x2﹣lnx上和直线y=x﹣2平行的切线经过的切点坐标为(1,1),
点(1,1)到直线y=x﹣2的距离等于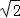 ,
,
∴点P到直线y=x﹣2的最小距离为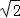 ,
,
故选:C.
已知α,β∈(0, ),且
),且  ,则下列结论正确的是( )
,则下列结论正确的是( )
A.α<β B.α+β> C.α>β D.α+β<
C.α>β D.α+β<
知识点:6.三角函数的图像与性质
C
【考点】函数单调性的性质.
【分析】由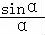 <
<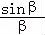 ,可得
,可得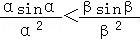 ,利用假设法,证明即可.设αsinα>βsinβ,则α>β,α,β∈(0,
,利用假设法,证明即可.设αsinα>βsinβ,则α>β,α,β∈(0,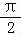 ),可得
),可得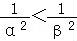 ,可得
,可得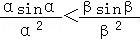 成立.可得结论.
成立.可得结论.
【解答】解:由 <
<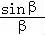 ,可得
,可得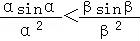 ,
,
∵α,β∈(0,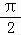 ),设αsinα>βsinβ>0,则α>β,
),设αsinα>βsinβ>0,则α>β,
∴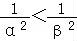 ,
,
∴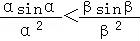 成立.
成立.
故得α>β,
故选C.
若圆(x﹣3)2+(y+5)2=r2上有且只有两个点到直线4x﹣3y=2的距离等于1,则半径r的取值范围是( )
A.(4,6) B.[4,6) C.(4,6] D.[4,6]
知识点:4.直线与圆的位置关系
A
【考点】点到直线的距离公式.
【分析】先利用点到直线的距离公式求出圆心到直线的距离,由题意得|5﹣r|<1,解此不等式求得半径r的取值范围.
【解答】解:∵圆心P(3,﹣5)到直线4x﹣3y=2的距离等于 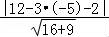 =5,由|5﹣r|<1得 4<r<6,
=5,由|5﹣r|<1得 4<r<6,
故选 A.
设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)<1,f(0)=11,则不等式f(x)> (其中e为自然对数的底数)的解集为( )
(其中e为自然对数的底数)的解集为( )
A.(10,+∞) B.(﹣∞,0)∪(11,+∞) C.(﹣∞,11) D.(﹣∞,0)
知识点:3.导数在研究函数中的应用
D
【考点】利用导数研究函数的单调性.
【分析】构造函数g(x)=exf(x)﹣ex,(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解.
【解答】解:设g(x)=exf(x)﹣ex,(x∈R),
则g′(x)=exf(x)+exf′(x)﹣ex=ex[f(x)+f′(x)﹣1],
∵f(x)+f′(x)<1,
∴f(x)+f′(x)﹣1<0,
∴g′(x)<0,
∴y=g(x)在定义域上单调递减,
∵f(x)>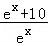 ,
,
∴exf(x)﹣ex>10,
∴g(x)>10,
又∵g(0)=e0f(0)﹣e0=11﹣1=10,
∴g(x)>g(0),
∴x<0,
∴不等式的解集为(﹣∞,0)
故选:D.
如图所示,图中曲线方程为y=x2﹣1,则围成封闭图形(阴影部分)的面积是 .

知识点:7.定积分的简单应用
2
【考点】定积分;定积分的简单应用.
【分析】利用定积分的几何意义表示阴影部分面积,然后计算定积分.
【解答】解:曲线方程为y=x2﹣1,则围成封闭图形(阴影部分)的面积是
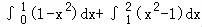 =(x﹣
=(x﹣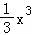 )|
)|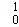 +(
+(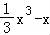 )|
)|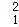 =2;
=2;
故答案为:2.
已知 =2
=2 ,
, =3
=3 ,
, =4
=4 ,…,若
,…,若 =7
=7 ,(a、b均为正实数),则类比以上等式,可推测a、b的值,进而可得a+b= .
,(a、b均为正实数),则类比以上等式,可推测a、b的值,进而可得a+b= .
知识点:1.合情推理与演绎推理
55
【考点】类比推理.
【分析】观察所给的等式,照此规律,第7个等式中:a=7,b=72﹣1=48,即可写出结果.
【解答】解:观察下列等式
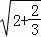 =2
=2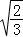 ,
,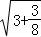 =3
=3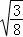 ,
, =4
=4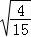 ,…,
,…,
照此规律,第7个等式中:a=7,b=72﹣1=48,
∴a+b=55,
故答案为:55
以抛物线y2=4x的焦点为顶点,顶点为中心,离心率为2的双曲线的渐近线方程为 .
知识点:3.抛物线
y= x
x
【考点】抛物线的简单性质;双曲线的简单性质.
【分析】求出抛物线的焦点坐标,得到双曲线的实半轴的长,利用离心率求解c,得到b,即可得到双曲线的渐近线方程.
【解答】解:抛物线y2=4x的焦点(1,0),可得a=1,离心率为2的双曲线,可得c=2,则b=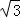 ,
,
双曲线的焦点坐标在x轴上,可得:双曲线的渐近线方程为:y=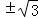 x.
x.
故答案为:y= x.
x.
设函数f(x)=ax3﹣3x+1(x∈R),若对于任意的x∈[﹣1,1]都有f(x)≥0成立,则实数a的值为 .
知识点:3.导数在研究函数中的应用
4
【考点】利用导数求闭区间上函数的最值.
【分析】先求出f′(x)=0时x的值,进而讨论函数的增减性得到f(x)的最小值,对于任意的x∈[﹣1,1]都有f(x)≥0成立,可转化为最小值大于等于0即可求出a的范围.
【解答】解:由题意,f′(x)=3ax2﹣3,
当a≤0时3ax2﹣3<0,函数是减函数,f(0)=1,只需f(1)≥0即可,解得a≥2,与已知矛盾,
当a>0时,令f′(x)=3ax2﹣3=0解得x=±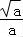 ,
,
①当x<﹣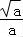 时,f′(x)>0,f(x)为递增函数,
时,f′(x)>0,f(x)为递增函数,
②当﹣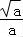 <x<
<x<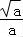 时,f′(x)<0,f(x)为递减函数,
时,f′(x)<0,f(x)为递减函数,
③当x>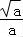 时,f(x)为递增函数.
时,f(x)为递增函数.
所以f(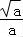 )≥0,且f(﹣1)≥0,且f(1)≥0即可
)≥0,且f(﹣1)≥0,且f(1)≥0即可
由f(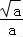 )≥0,即a•
)≥0,即a•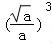 ﹣3•
﹣3•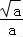 +1≥0,解得a≥4,
+1≥0,解得a≥4,
由f(﹣1)≥0,可得a≤4,
由f(1)≥0解得2≤a≤4,
综上a=4为所求.
故答案为:4.
设函数f(x)=(1+x)2﹣2ln(1+x).
(Ⅰ)对任意x0∈[0,1],不等式f(x0)﹣m≤0恒成立,求实数m的最小值;
(Ⅱ)若存在x0∈[0,1],使不等式f(x0)﹣m≤0成立,求实数m的取值范围.
知识点:3.导数在研究函数中的应用
【考点】函数恒成立问题.
【分析】(Ⅰ)利用导数可判断出:当x∈[0,1]时,f′(x)≥0,故f(x)在区间[0,1]上单调递增,从而可求得f(x)max,由m≥f(x)max即可求得实数m的最小值;
(Ⅱ)若存在x0∈[0,1],使不等式f(x0)﹣m≤0成立⇔m≥f(x)min,由(Ⅰ)知f(x)在区间[0,1]上单调递增,可求得f(x)min,从而可求得实数m的取值范围.
【解答】解:(Ⅰ)∵f′(x)=2(1+x)﹣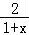 =
=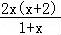 ,
,
当x∈[0,1]时,f′(x)≥0,故f(x)在区间[0,1]上单调递增,
所以f(x)max=f(1)=4﹣2ln2,
不等式f(x0)﹣m≤0恒成立,等价于m≥f(x)max=4﹣2ln2,
所以m最小值为4﹣2ln2.
(Ⅱ)由(Ⅰ)知,(x)在区间[0,1]上单调递增,
故当x0∈[0,1],时f(x0)min=f(0)=1,
若存在x0∈[0,1],使不等式f(x0)﹣m≤0成立,等价于m≥f(x)min=1,
所以m的取值范围为[1,+∞).
已知函数f(x)=alnx﹣ax﹣3(a∈R).
(1)若a=﹣1,求函数f(x)的单调区间并比较f(x)与f(1)的大小关系
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2[f′(x)+ ]在区间(t,3)上总不是单调函数,求m的取值范围.
]在区间(t,3)上总不是单调函数,求m的取值范围.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.
【分析】(1)当a=﹣1时,求出f′(x),解不等式f′(x)>0,f′(x)<0,可得单调区间,根据最值情况可比较f(x)与f(1)的大小关系;
(2)由函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,可求出a值,对于任意的t∈[1,2],函数g(x)在区间(t,3)上总不单调,则g(x)在区间(t,3)内总存在极值点,由此可得到关于m的约束条件,解出即可.
【解答】解:(1)当a=﹣1时,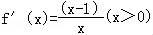 ,
,
解f'(x)>0,得x∈(1,+∞);解f'(x)<0得x∈(0,1),
所以,f(x)的单调增区间为(1,+∞),减区间为(0,1),
可知f(x)min=f(1),所以f(x)≥f(1).
(2)∵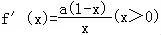 ,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
∴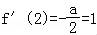 ,得a=﹣2,f(x)=﹣2lnx+2x﹣3,
,得a=﹣2,f(x)=﹣2lnx+2x﹣3,
∴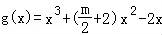 ,∴g'(x)=3x2+(m+4)x﹣2,
,∴g'(x)=3x2+(m+4)x﹣2,
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=﹣2,∴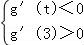 ,
,
由题意知:对于任意的t∈[1,2],g'(t)<0恒成立,
所以有,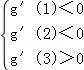 ,解得
,解得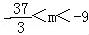 .
.
故m的取值范围为(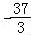 ,﹣9).
,﹣9).
设函数f(x)=lnx+ ,m∈R
,m∈R
(1)当m=e(e为自然对数的底数)时,求f(x)的最小值;
(2)讨论函数g(x)=f′(x)﹣ 零点的个数;
零点的个数;
(3)(理科)若对任意b>a>0, <1恒成立,求m的取值范围.
<1恒成立,求m的取值范围.
知识点:3.导数在研究函数中的应用
【考点】导数在最大值、最小值问题中的应用;根的存在性及根的个数判断;利用导数研究函数的极值.
【分析】(1)当m=e时,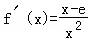 ,x>0,由此利用导数性质能求出f(x)的极小值.
,x>0,由此利用导数性质能求出f(x)的极小值.
(2)由g(x)=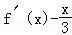 =
=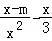 =0,得m=
=0,得m=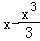 ,令h(x)=x﹣
,令h(x)=x﹣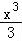 ,x>0,m∈R,则h(1)=
,x>0,m∈R,则h(1)=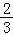 ,h′(x)=1﹣x2=(1+x)(1﹣x),由此利用导数性质能求出函数g(x)=f′(x)﹣
,h′(x)=1﹣x2=(1+x)(1﹣x),由此利用导数性质能求出函数g(x)=f′(x)﹣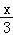 零点的个数.
零点的个数.
(3)(理)当b>a>0时,f′(x)<1在(0,+∞)上恒成立,由此能求出m的取值范围.
【解答】解:(1)当m=e时,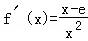 ,x>0,
,x>0,
解f′(x)>0,得x>e,
∴f(x)单调递增;
同理,当0<x<e时,f′(x)<0,f(x)单调递减,
∴f(x)只有极小值f(e),
且f(e)=lne+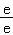 =2,
=2,
∴f(x)的极小值为2.
(2)∵g(x)=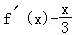 =
= =0,
=0,
∴m=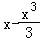 ,
,
令h(x)=x﹣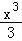 ,x>0,m∈R,
,x>0,m∈R,
则h(1)= ,h′(x)=1﹣x2=(1+x)(1﹣x),
,h′(x)=1﹣x2=(1+x)(1﹣x),
令h′(x)>0,解得0<x<1,
∴h(x)在区间(0,1)上单调递增,值域为(0, );
);
同理,令h′(x)<0,解得x>1,
∴g(x)要区是(1,+∞)上单调递减,值域为(﹣∞, ).
).
∴当m≤0,或m=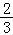 时,g(x)只有一个零点;
时,g(x)只有一个零点;
当0<m<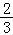 时,g(x)有2个零点;
时,g(x)有2个零点;
当m>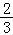 时,g(x)没有零点.
时,g(x)没有零点.
(3)(理)对任意b>a>0,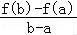 <1恒成立,
<1恒成立,
等价于f(b)﹣b<f(a)﹣a恒成立;
设h(x)=f(x)﹣x=lnx+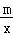 ﹣x(x>0),
﹣x(x>0),
则h(b)<h(a).
∴h(x)在(0,+∞)上单调递减;
∵h′(x)=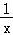 ﹣
﹣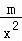 ﹣1≤0在(0,+∞)上恒成立,
﹣1≤0在(0,+∞)上恒成立,
∴m≥﹣x2+x=﹣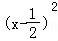 +
+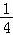 (x>0),
(x>0),
∴m≥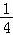 ;
;
对于m=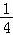 ,h′(x)=0仅在x=
,h′(x)=0仅在x= 时成立;
时成立;
∴m的取值范围是[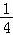 ,+∞).
,+∞).
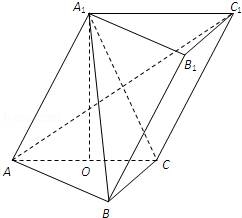
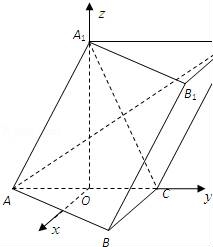
如图,在三棱柱ABC﹣A1B1C1中,四边形AA1C1C是边长为2的菱形,平面ABC⊥平面AA1C1C,∠A1AC=60°,∠BCA=90°.
(Ⅰ)求证:A1B⊥AC1;
(Ⅱ)已知点E是AB的中点,BC=AC,求直线EC1与平面ABB1A1所成的角的正弦值.

知识点:6.直线、平面垂直的判定及其性质
【考点】直线与平面所成的角;空间中直线与直线之间的位置关系.
【分析】(Ⅰ)首先利用面面垂直转化成线面垂直,进一步得出线线垂直.
(Ⅱ)根据两两垂直的关系,建立空间直角坐标系,求出平面的法向量,进一步利用向量的夹角余弦公式求出线面的夹角的正弦值.
【解答】(Ⅰ)证明:取AC的中点O,连接A1O,
由于平面ABC⊥平面AA1C1C,A1O⊥AC,
所以:A1O⊥平面ABC,
所以:A1O⊥BC,
又BC⊥AC,
所以:BC⊥平面A1AC,
又AC1⊥A1C,A1C为A1B的射影,
所以:A1B⊥AC1.
(Ⅱ)以O为坐标原点建立空间直角坐标系O﹣xyz,
A(0,﹣1,0),B(2,1,0),C(0,1,0),C1(0,2,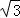 ),
),
则: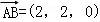 ,
,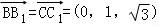 ,
,
设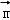 =(x,y,z)是平面ABB1A1的法向量,
=(x,y,z)是平面ABB1A1的法向量,
所以: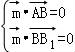 ,
,
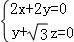
求得: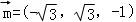 ,
,
由E(1,0,0)
求得: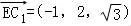 ,
,
直线EC1与平面ABB1A1所成的角的正弦值
sinθ=cos =
=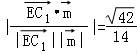 .
.
已知动圆P与圆F1:(x+1)2+y2=1外切,与圆F2:(x﹣1)2+y2=9内切.动圆P的圆心轨迹为曲线E,且曲线E与y轴的正半轴相交于点M.若曲线E上相异两点A、B满足直线MA,MB的斜率之积为 .
.
(1)求E的方程;
(2)证明直线AB恒过定点,并求定点的坐标.
知识点:4.直线与圆的位置关系
【考点】轨迹方程.
【分析】(1)确定PF1|+|PF2|=4>|F1F2|,可得曲线E是长轴长2a=4,焦距2c=2的椭圆,且b2=a2﹣c2=3,即可求E的方程;
(2)分类讨论,设直线方程,代入椭圆方程,利用韦达定理,结合直线MA,MB的斜率之积为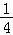 ,即可证明直线AB恒过定点,并求定点的坐标
,即可证明直线AB恒过定点,并求定点的坐标
【解答】解 (1)设动圆P的半径为r,由已知|PF1|=r+1,|PF2|=3﹣r,
则有|PF1|+|PF2|=4,化简得曲线E的方程为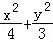 =1.
=1.
(2)由曲线E的方程得,上顶点M(0,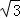 ),记A(x1,y1),B(x2,y2),由题意知,x1≠0,x2≠0.若直线AB的斜率不存在,则直线AB的方程为x=x1,故y1=﹣y2,
),记A(x1,y1),B(x2,y2),由题意知,x1≠0,x2≠0.若直线AB的斜率不存在,则直线AB的方程为x=x1,故y1=﹣y2,
因此,kMA•kMB=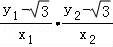 =﹣
=﹣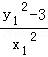 =
=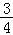 ,
,
与已知不符,因此直线AB的斜率存在.
设直线AB:y=kx+m,代入椭圆E的方程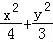 =1,得
=1,得
(3+4k2)x2+8kmx+4(m2﹣3)=0,①
因为直线AB与曲线E有公共点A,B,所以方程①有两个非零不等实根x1,x2,
所以x1+x2=﹣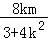 ,x1•x2=
,x1•x2=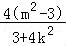 ,
,
又kAM=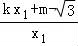 ,kMB=
,kMB=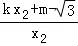
由kAM•kBM=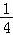 得4(kx1+m﹣
得4(kx1+m﹣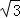 )(kx2+m﹣
)(kx2+m﹣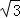 )=x1x2,
)=x1x2,
即(4k2﹣1)x1x2+4k(m﹣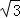 )(x1+x2)+4(m﹣
)(x1+x2)+4(m﹣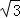 )2=0,
)2=0,
所以4(m2﹣3)(4k2﹣1)+4k(m﹣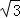 )(﹣8km)+4(m﹣
)(﹣8km)+4(m﹣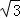 )2•(3+4k2)=0,
)2•(3+4k2)=0,
化简得m2﹣3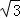 +6=0,故m=
+6=0,故m=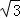 或m=2
或m=2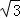 .
.
结合x1x2≠0知m=2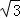 ,即直线AB恒过定点N(0,2
,即直线AB恒过定点N(0,2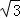 ).
).
已知函数f(x)=x2+ax﹣lnx.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设g(x)=f(x)+2lnx,F(x)=3g(x)﹣2xg′(x),若函数F(x)在定义域内有两个零点x1,x2,且x1<x2,求证:F′( )<0.
)<0.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性.
【分析】(Ⅰ)求导根据导数和函数的单调性的关系即可求出,
(Ⅱ)求导,根据中点坐标公式得到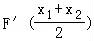 =﹣(x1+x2)+a+
=﹣(x1+x2)+a+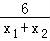 ,①,分别把两个零点x1,x2,代入到F(x)中,转化,分离参数得到a﹣(x1+x2)=
,①,分别把两个零点x1,x2,代入到F(x)中,转化,分离参数得到a﹣(x1+x2)=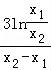 ,再代入得到
,再代入得到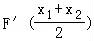 =
=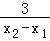 [ln
[ln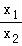 +
+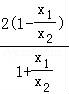 ],换元,构造函数得到h(t)=lnt+
],换元,构造函数得到h(t)=lnt+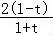 ,根据导数求出h(t)的最大值,即可证明.
,根据导数求出h(t)的最大值,即可证明.
【解答】解:(Ⅰ)函数的定义域为(0,+∞),
∴f′(x)=2x+a﹣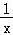 =
=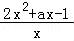 ,
,
令f′(x)>0,得x>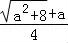 ,
,
f′(x)<0,得0<x<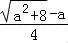 ,
,
∴函数f(x)在(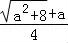 ,+∞)为增函数,在(0,
,+∞)为增函数,在(0,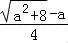 )为减函数,
)为减函数,
(Ⅱ)由已知g(x)=f(x)+2lnx,
∴F(x)=3g(x)﹣2xg′(x)=﹣x2+ax+3lnx﹣2,
∴F′(x)=﹣2x+a+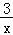 ,
,
即: =﹣(x1+x2)+a+
=﹣(x1+x2)+a+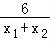 ,①
,①
∵函数F(x)在定义域内有两个零点x1,x2,
∴﹣x12+ax1+3lnx1﹣2=0,②
﹣x22+ax2+3lnx2﹣2=0,③
②﹣③得﹣(x12﹣x22)+a(x1﹣x2)+3(lnx1﹣lnx2)=0
可得(x1﹣x2)[a﹣(x1+x2)]+3ln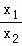 =0,
=0,
∴a﹣(x1+x2)=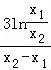 ,
,
代入①得: =
=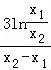 +
+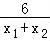 =
=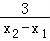 [ln
[ln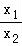 +
+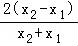 ]=
]=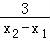 [ln
[ln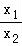 +
+ ],
],
令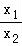 =t,则0<t<1,
=t,则0<t<1,
∴h(t)=lnt+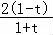 ,
,
∴h′(t)=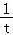 +
+ =
=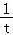 ﹣
﹣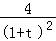 =
=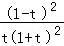 ≥0
≥0
∴h(t)在(0,1)上为增函数,
∴h(t)<h(1)=0,
∵x1<x2,
∴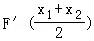 <0.
<0.