已知集合A={x|x2+x﹣2<0}, ,则A∩B=( )
,则A∩B=( )
A. B.(0,1) C.
B.(0,1) C. D.
D.
知识点:3.集合的基本运算
A
【考点】交集及其运算.
【分析】先分别出集合A,B,由此利用交集定义能求出A∩B.
【解答】解:∵集合A={x|x2+x﹣2<0}={x|﹣2<x<1},
 ={x|0<x<
={x|0<x< },
},
∴A∩B={x|0<x<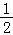 }=(0,
}=(0,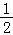 ).
).
故选:A.
已知等比数列{an}的公比为q,则“0<q<1”是“{an}为递减数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
知识点:5.充分条件与必要条件
D
【考点】必要条件、充分条件与充要条件的判断.
【分析】可举﹣1,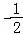 ,
,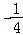 …,说明不充分;举等比数列﹣1,﹣2,﹣4,﹣8,…说明不必要,进而可得答案.
…,说明不充分;举等比数列﹣1,﹣2,﹣4,﹣8,…说明不必要,进而可得答案.
【解答】解:可举a1=﹣1,q=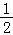 ,可得数列的前几项依次为﹣1,
,可得数列的前几项依次为﹣1,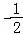 ,
,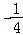 …,显然不是递减数列,
…,显然不是递减数列,
故由“0<q<1”不能推出“{an}为递减数列”;
可举等比数列﹣1,﹣2,﹣4,﹣8,…显然为递减数列,但其公比q=2,不满足0<q<1,
故由“{an}为递减数列”也不能推出“0<q<1”.
故“0<q<1”是“{an}为递减数列”的既不充分也不必要条件.
故选D
已知α,β,γ是三个不同的平面,l1,l2是两条不同的直线,下列命题是真命题的是( )
A.若α⊥γ,β⊥γ,则α∥β B.若l1∥α,l1⊥β,则α∥β
C.若α∥β,l1∥α,l2∥β,则l1∥l2 D.若α⊥β,l1⊥α,l2⊥β,则l1⊥l2
E.若α⊥β,l1⊥α,l2⊥β,则l1⊥l2 F.若α⊥β,l1⊥α,l2⊥β,则l1⊥l2
知识点:4.空间点、直线、平面之间的位置关系
D
【考点】空间中直线与平面之间的位置关系;平面与平面之间的位置关系.
【分析】反例判断A的错误;利用直线与平面的关系判断B错误;反例判断C错误;直线与平面垂直判断D正误即可.
【解答】解:α,β,γ是三个不同的平面,l1,l2是两条不同的直线,
对于A,α⊥γ,β⊥γ,则α∩β=a也可能平行,所以A不正确.
对于B,若l1∥α,l1⊥β,则α⊥β,所以B不正确;
对于C,α∥β,l1∥α,l2∥β,则l1∥l2,也可能相交也可能异面,所以C不正确;
对于D,若α⊥β,l1⊥α,l2⊥β,则l1⊥l2,l1与l2是平面的法向量,显然正确;
故选:D.
直线ax+y﹣5=0截圆C:x2+y2﹣4x﹣2y+1=0的弦长为4,则a=( )
A.﹣2 B.﹣3 C.2 D.3
知识点:4.直线与圆的位置关系
C
【考点】直线与圆的位置关系.
【分析】圆C:x2+y2﹣4x﹣2y+1=0配方为:(x﹣2)2+(y﹣1)2=4,可得圆心C(2,1),半径r=2.直线ax+y﹣5=0截圆C:x2+y2﹣4x﹣2y+1=0的弦长为4,可得直线经过圆心.
【解答】解:圆C:x2+y2﹣4x﹣2y+1=0配方为:(x﹣2)2+(y﹣1)2=4,可得圆心C(2,1),半径r=2.
∵直线ax+y﹣5=0截圆C:x2+y2﹣4x﹣2y+1=0的弦长为4,
∴直线经过圆心,∴2a+1﹣5=0,解得a=2.
故选:C.
下列命题中错误的个数为:( )
①y= 的图象关于(0,0)对称;
的图象关于(0,0)对称;
②y=x3+x+1的图象关于(0,1)对称;
③y= 的图象关于直线x=0对称;
的图象关于直线x=0对称;
④y=sinx+cosx的图象关于直线x= 对称.
对称.
A.0 B.1 C.2 D.3
知识点:15.函数的图像
A
【考点】函数的图象.
【分析】根据函数的奇偶性判断,①③,根据对称的定义判断②,根据三角函数的图象判断④
【解答】解:①y=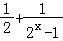 ,f(﹣x)=
,f(﹣x)=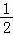 +
+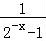 =
=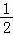 +
+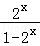 =
=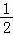 ﹣
﹣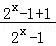 =﹣
=﹣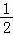 ﹣
﹣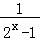 =﹣(
=﹣(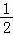 +
+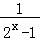 )=﹣f(x),
)=﹣f(x),
∴函数为奇函数,则图象关于(0,0)对称,故正确
②y=x3+x+1的图象关于(0,1)对称;
由题意设对称中心的坐标为(a,b),
则有2b=f(a+x)+f(a﹣x)对任意x均成立,代入函数解析式得,
2b=(a+x)3+3(a+x)+1+(a﹣x)3+3(a﹣x)+1对任意x均成立,
∴a=0,b=1
即对称中心(0,1),故正确
③y= 的图象关于直线x=0对称,因为函数为偶函数,故函数关于y轴(x=0)对称,故正确,
的图象关于直线x=0对称,因为函数为偶函数,故函数关于y轴(x=0)对称,故正确,
④y=sinx+cosx=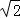 sin(x+
sin(x+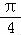 )的图象关于直线x+
)的图象关于直线x+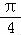 =
=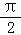 对称,即x=
对称,即x=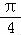 对称,故正确.
对称,故正确.
故选:A
如图是某多面体的三视图,网格纸上小正方形的边长为1,则该多面体的体积为( )

A.32 B. C.16 D.
C.16 D.
知识点:2.空间几何体的三视图和直观图
D
【考点】由三视图求面积、体积.
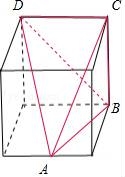
【分析】如图所示,该几何体为三棱锥A﹣BCD,其外面图形为棱长为4的正方体.
【解答】解:如图所示,该几何体为三棱锥A﹣BCD,其外面图形为棱长为4的正方体.
∴该多面体的体积V=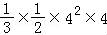 =
=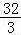 .
.
故选:D.
设函数f(x)=sin(ωx+φ)﹣ cos(ωx+φ)(ω>0,|φ|<
cos(ωx+φ)(ω>0,|φ|< )的最小正周期为π,且f(﹣x)=f(x),则( )
)的最小正周期为π,且f(﹣x)=f(x),则( )
A.f(x)在(0, )单调递减 B.f(x)在(
)单调递减 B.f(x)在( ,
, )单调递减
)单调递减
C.f(x)在(0, )单调递增 D.f(x)在(
)单调递增 D.f(x)在( ,
, )单调递增
)单调递增
知识点:7.函数y=Asin(wx+@)+B
C
【考点】三角函数的周期性及其求法.
【分析】利用辅助角公式化积,由周期求得ω,再由函数为偶函数求得φ,求出函数解析式得答案.
【解答】解:f(x)=sin(ωx+φ)﹣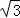 cos(ωx+φ)=2sin(ωx+φ﹣
cos(ωx+φ)=2sin(ωx+φ﹣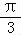 ).
).
由T=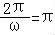 ,得ω=2.
,得ω=2.
∴f(x)=2sin(2x+φ﹣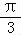 ).
).
又f(﹣x)=f(x),∴sin(﹣2x+φ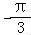 )=2sin(2x+φ﹣
)=2sin(2x+φ﹣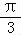 ).
).
得﹣2x+φ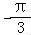 =2x+φ﹣
=2x+φ﹣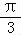 +2kπ或﹣2x+φ
+2kπ或﹣2x+φ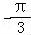 +2x+φ﹣
+2x+φ﹣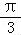 =π+2kπ,k∈Z.
=π+2kπ,k∈Z.
解得φ=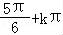 ,k∈Z.
,k∈Z.
∵|φ|<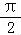 ,∴φ=
,∴φ=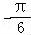 .
.
∴f(x)=2sin(2x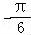 ﹣
﹣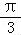 )=2sin(2x﹣
)=2sin(2x﹣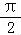 )=﹣2cos2x.
)=﹣2cos2x.
则f(x)在(0,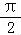 )单调递增.
)单调递增.
故选:C.
已知a>0,b>0,且 为3a与3b的等比中项,则
为3a与3b的等比中项,则 的最大值为( )
的最大值为( )
A. B.
B. C.
C. D.
D.
知识点:4.等比数列及其性质
B
【考点】等比数列的通项公式;基本不等式.
【分析】由等比中项推导出a+b=1,从而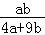 =
= =
=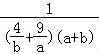 =
=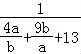 ,由此利用基本不等式能求出
,由此利用基本不等式能求出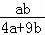 的最大值.
的最大值.
【解答】解:∵a>0,b>0,且 为3a与3b的等比中项,
为3a与3b的等比中项,
∴3a•3b=3a+b=( )2=3,
)2=3,
∴a+b=1,
∴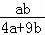 =
=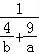 =
=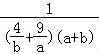 =
=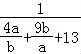 ≤
≤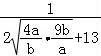 =
=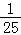 .
.
当且仅当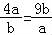 时,取等号,
时,取等号,
∴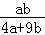 的最大值为
的最大值为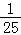 .
.
故选:B.
若函数f(x)为定义在R上的连续奇函数且3f(x)+xf′(x)>0对x>0恒成立,则方程x3f(x)=﹣1的实根个数为( )
A.0 B.1 C.2 D.3
知识点:3.导数在研究函数中的应用
B
【考点】函数恒成立问题.
【分析】可构造函数g(x)=x3f(x),利用导数判断其单调性,结合函数为奇函数,即可得出结论.
【解答】解:令g(x)=x3f(x),则g′(x)=x2[3f(x)+xf′(x)],
∵3f(x)+xf′(x)>0对x>0恒成立,
∴g′(x)>0,
∴当x>0时,g(x)为增函数,
又∵函数f(x)是定义在R上的奇函数,
∴g(x)为R上的增函数,
∴方程x3f(x)=﹣1的实根个数为1.
故选:B.
在直三棱柱ABC﹣A1B1C1中,侧棱长为 ,在底面△ABC中,∠C=60°,
,在底面△ABC中,∠C=60°, ,则此直三棱柱的外接球的表面积为( )
,则此直三棱柱的外接球的表面积为( )
A. B.
B. C.16π D.
C.16π D.
知识点:3.空间几何体的表面积与体积
C
【考点】球的体积和表面积.
【分析】由题意可知直三棱柱ABC﹣A1B1C1中,底面ABC的小圆半径为1,连接两个底面中心的连线,中点与顶点的连线就是球的半径,即可求出球的表面积.
【解答】解:由题意可知直三棱柱ABC﹣A1B1C1中,底面小圆ABC的半径为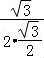 =1,
=1,
连接两个底面中心的连线,中点与顶点的连线就是球的半径,外接球的半径为: =2,
=2,
外接球的表面积为:4π•22=16π.
故选C.
已知椭圆C: +
+ =1(a>b>0),点M,N,F分别为椭圆C的左顶点、上顶点、左焦点,若∠MFN=∠NMF+90°,则椭圆C的离心率是( )
=1(a>b>0),点M,N,F分别为椭圆C的左顶点、上顶点、左焦点,若∠MFN=∠NMF+90°,则椭圆C的离心率是( )
A. B.
B. C.
C. D.
D.
知识点:1.椭圆
A
【考点】椭圆的简单性质.
【分析】由题意画出图形,结合已知可得a,b,c的关系,进一步结合隐含条件可得关于离心率e的方程求解.
【解答】解:如图,
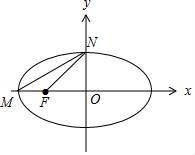
tan∠NMF=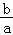 ,tan∠NFO=
,tan∠NFO=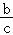 ,
,
∵∠MFN=∠NMF+90°,∴∠NFO=180°﹣MFN=90°﹣∠NMF,
即tan∠NFO=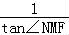 ,
,
∴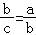 ,则b2=a2﹣c2=ac,
,则b2=a2﹣c2=ac,
∴e2+e﹣1=0,得e=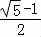 .
.
故选:A.
已知函数f(x)= ,若当方程f(x)=m有四个不等实根x1,x2,x3,x4(x1<x2<x3<x4)时,不等式kx3x4+x12+x22≥k+11恒成立,则实数k的最小值为 ( )
,若当方程f(x)=m有四个不等实根x1,x2,x3,x4(x1<x2<x3<x4)时,不等式kx3x4+x12+x22≥k+11恒成立,则实数k的最小值为 ( )
A. B.2﹣
B.2﹣ C.
C. D.
D. ﹣
﹣
知识点:13.函数与方程
B
【考点】函数的最值及其几何意义;函数恒成立问题;分段函数的应用.
【分析】画出函数f(x)= 的图象,结合对数函数的图象和性质,可得x1•x2=1,x1+x2>
的图象,结合对数函数的图象和性质,可得x1•x2=1,x1+x2>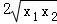 =2,(4﹣x3)•(4﹣x4)=1,且x1+x2+x3+x4=8,则不等式kx3x4+x12+x22≥k+11恒成立,可化为:k≥
=2,(4﹣x3)•(4﹣x4)=1,且x1+x2+x3+x4=8,则不等式kx3x4+x12+x22≥k+11恒成立,可化为:k≥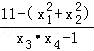 恒成立,求出
恒成立,求出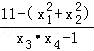 的最大值,可得k的范围,进而得到实数k的最小值.
的最大值,可得k的范围,进而得到实数k的最小值.
【解答】解:函数f(x)= 的图象如下图所示:
的图象如下图所示:

当方程f(x)=m有四个不等实根x1,x2,x3,x4(x1<x2<x3<x4)时,
|lnx1|=|lnx2|,即x1•x2=1,x1+x2>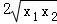 =2,
=2,
|ln(4﹣x3)|=|(4﹣x4)|,即(4﹣x3)•(4﹣x4)=1,
且x1+x2+x3+x4=8,
若不等式kx3x4+x12+x22≥k+11恒成立,
则k≥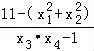 恒成立,
恒成立,
由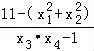 =
=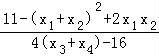 =
=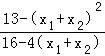 =
=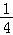 [(x1+x2)﹣4
[(x1+x2)﹣4 +8]≤2﹣
+8]≤2﹣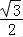
故k≥2﹣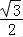 ,
,
故实数k的最小值为2﹣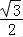 ,
,
故选:B
已知向量 ,
, 满足
满足 ,|
,| ,且
,且 (λ>0),则λ= .
(λ>0),则λ= .
知识点:4.平面向量的数量积(夹角、模)
2
【考点】平面向量数量积的运算.
【分析】根据条件即可求出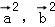 的值,而由
的值,而由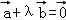 可得到
可得到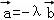 ,两边平方即可得到关于λ的方程,解出λ即可.
,两边平方即可得到关于λ的方程,解出λ即可.
【解答】解: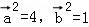 ;
;
由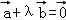 得,
得,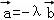 ;
;
∴ ;
;
∴4=λ2,且λ>0;
∴λ=2.
故答案为:2.
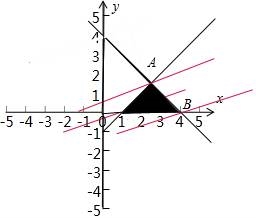
设x,y满足约束条件 则z=x﹣3y的取值范围为 .
则z=x﹣3y的取值范围为 .
知识点:3.二元一次不等式(组)与简单的线性规划
[﹣2,4]
【考点】简单线性规划.
【分析】由约束条件作出可行域,联立方程组求出最优解的坐标,代入目标函数得答案.
【解答】解:由约束条件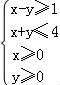 作出可行域如图,
作出可行域如图,
联立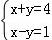 ,解得A(
,解得A( ,
,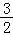 ),
),
联立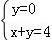 ,解得B(4,0),
,解得B(4,0),
由图可知,当目标函数z=x﹣3y过A时,z有最小值为﹣2;
当目标函数z=x﹣3y过B时,z有最大值为:4.
故答案为:[﹣2,4].
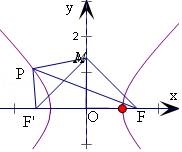
已知双曲线C: 的右焦点为F,P是双曲线C的左支上一点,M(0,2),则△PFM周长最小值为 .
的右焦点为F,P是双曲线C的左支上一点,M(0,2),则△PFM周长最小值为 .
知识点:2.双曲线
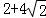
【考点】直线与双曲线的位置关系;双曲线的简单性质.
【分析】设双曲线的左焦点为F',求出双曲线的a,b,c,运用双曲线的定义可得|PA|+|PF|=|PA|+|PF'|+2,考虑P在左支上运动到与A,F'共线时,取得最小值,即可得到所求值.
【解答】解:设双曲线的左焦点为F',
由双曲线C: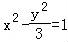 可得a=1,b=
可得a=1,b=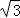 ,c=2,
,c=2,
即有F(2,0),F'(﹣2,0),
△PFM周长为|PM|+|PF|+|MF|=|PM|+|PF|+2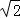 ,
,
由双曲线的定义可得|PF|﹣|PF'|=2a=2,
即有|PM|+|PF|=|PM|+|PF'|+2,
当P在左支上运动到M,P,F'共线时,
|PM|+|PF'|取得最小值|MF'|=2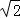 ,
,
则有△APF周长的最小值为2+2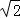 +2
+2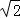 =2+4
=2+4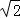 .
.
故答案为: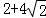
若Sn为数列{an}的前n项和,且2Sn=an+1an,a1=4,则数列{an}的通项公式为an= .
知识点:7.数列的通项
【考点】数列递推式.
【分析】2Sn=an+1an,a1=4,n=1时,2×4=4a2,解得a2.n≥2时,2Sn﹣1=anan﹣1,可得2an=an+1an﹣anan﹣1,可得an+1﹣an﹣1=2.n≥2时,an+1﹣an﹣1=2,可得数列{an}的奇数项与偶数项分别为等差数列.
【解答】解:∵2Sn=an+1an,a1=4,
∴n=1时,2×4=4a2,解得a2=2.
n≥2时,2Sn﹣1=anan﹣1,可得2an=an+1an﹣anan﹣1,
∴an=0(舍去),或an+1﹣an﹣1=2.
n≥2时,an+1﹣an﹣1=2,可得数列{an}的奇数项与偶数项分别为等差数列.
∴a2k﹣1=4+2(k﹣1)=2k+2.k∈N*.
a2k=2+2(k﹣1)=2k.
∴an=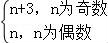 .
.
故答案为: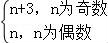 .
.
已知在△ABC中,内角A,B,C的对边分别为a,b,c,且acosC,bcosA,ccosA成等差数列.
(1)求角A的大小;
(2)若a=3, ,求
,求 的最大值.
的最大值.
知识点:9.正弦定理和余弦定理(解三角形)
【考点】余弦定理;正弦定理.
【分析】(1)由等差数列的性质可得2bcosA=acosC+ccosA,由正弦定理,三角形内角和定理化简可得sinB=2sinBcosA,结合sinB≠0,可求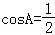 ,即可得解
,即可得解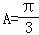 .
.
(2)利用平面向量的运算,余弦定理可得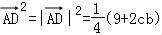 ,进而利用基本不等式即可计算得解.
,进而利用基本不等式即可计算得解.
【解答】解:(1)∵由题意知2bcosA=acosC+ccosA,
由正弦定理知sinAcosC+sinCcosA=2sinBcosA,
∴sin(A+C)=sinB=2sinBcosA,
又∵sinB≠0,
∴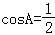 ,
,
∴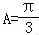 .
.
(2)∵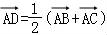 ,
,
∴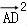 =
=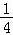 (
(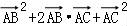 )=
)=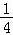 (c2+b2+2cbcosA)=
(c2+b2+2cbcosA)=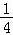 (c2+b2+cb),
(c2+b2+cb),
又∵由余弦定理可得:a2=c2+b2﹣2cbcosA=c2+b2﹣cb=9,
∴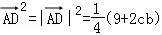 ,
,
∵由c2+b2﹣cb=9≥2cb﹣cb=cb,当且仅当c=b时取等号,
∴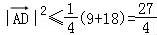 ,
,
∴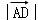 的最大值为
的最大值为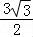 .
.
重庆八中大学城校区与本部校区之间的驾车单程所需时间为T,T只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
T(分钟)
25
30
35
40
频数(次)
100
150
200
50
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求T的分布列与P(T<E(T));
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记X表示这3位教师中驾车所用时间少于E(T)的人数,求X的分布列与E(X);
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.
知识点:7.独立重复试验与二项分布
【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.
【分析】(1)以频率估计频率,即可取得T的分布列.求出期望,得到概率即可.
(2)判断分布列是二项分布,然后列出分布列求出期望.
(3)设T1,T2分别表示往返所需时间,设事件A表示“从离开大学城校区到返回大学城校区共用时间不超过120分钟”,则P(A)=P(T1=25)P(T2≤45)+P(T1=30)P(T2≤40)+P(T1=35)P(T2≤35)+P(T1=40)P(T2≤30)求解即可.
【解答】解:(1)以频率估计频率得T的分布列为:
T | 25 | 30 | 35 | 40 |
P | 0.2 | 0.3 | 0.4 | 0.1 |
∴E(T)=25×0.2+30×0.3+35×0.4+40×0.1=32(分钟),
P(T<E(T))=P(T<32)=0.2+0.3=0.5.
(2)X~B(3,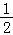 ),P(X=k)=
),P(X=k)=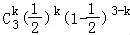 (k=0,1,2,3).
(k=0,1,2,3).
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(X)=3× =
=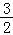 .
.
(3)设T1,T2分别表示往返所需时间,设事件A表示“从离开大学城校区到返回大学城校区共用时间不超过120分钟”,则
P(A)=P(T1=25)P(T2≤45)+P(T1=30)P(T2≤40)+P(T1=35)P(T2≤35)+P(T1=40)P(T2≤30)=0.2×1+0.3×1+0.4×0.9+0.1×0.5=0.91.
如图,在三棱台ABC﹣A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1,M,N分别为AC,BC的中点.
(1)求证:AB1∥平面C1MN;
(2)若AB⊥BC且AB=BC,求二面角C﹣MC1﹣N的大小.

知识点:5.直线、平面平行的判定及其性质
【考点】二面角的平面角及求法;直线与平面平行的判定.
【分析】(1)连接B1N,B1C,设B1C与NC1交于点G,推导出四边形B1C1CN是平行四边形,从而MG∥AB1,由此能证明AB1∥平面C1MN.
(2)以点M为坐标原点,MA,MB,MA1所在的直线分别为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角C﹣MC1﹣N的大小.
【解答】证明:(1)连接B1N,B1C,
设B1C与NC1交于点G,在三棱台ABC﹣A1B1C1中,
AB=2A1B1,则BC=2B1C1,
而N是BC的中点,B1C1∥BC,
则B1C1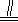 NC,所以四边形B1C1CN是平行四边形,G是B1C的中点,
NC,所以四边形B1C1CN是平行四边形,G是B1C的中点,
在△AB1C中,M是AC的中点,则MG∥AB1,
又AB1⊄平面C1MN,MG⊂平面C1MN,
所以AB1∥平面C1MN.
解:(2)由CC1⊥平面ABC,可得A1M⊥平面ABC,
而AB⊥BC,AB=BC,则MB⊥AC,
所以MA,MB,MA1两两垂直,
故以点M为坐标原点,MA,MB,MA1所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系.
设AB=2,则A1B1=CC1=1,AC=2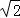 ,AM=
,AM=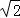 ,
,
B(0,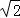 ,0),C(﹣
,0),C(﹣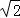 ,0,0),C1(﹣
,0,0),C1(﹣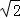 ,0,1),N(﹣
,0,1),N(﹣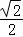 ,
,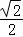 ,0),
,0),
则平面ACC1A1的一个法向量为 =(0,1,0),
=(0,1,0),
设平面C1MN的法向量为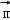 =(x,y,z),
=(x,y,z),
则 ,
,
取x=1,则 =(1,1,
=(1,1,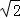 ),
),
cos<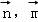 >=
>= ,
,
由图形得得二面角C﹣MC1﹣N为锐角,
所以二面角C﹣MC1﹣N的大小为60°.
在直角坐标系xOy中,点P(2,1)为抛物线C:y= 上的定点,A,B为抛物线C上两个动点.
上的定点,A,B为抛物线C上两个动点.
(1)若直线PA与PB的倾斜角互补,证明:直线AB的斜率为定值;
(2)若PA⊥PB,直线AB是否经过定点?若是,求出该定点,若不是,说明理由.
知识点:3.抛物线
【考点】直线与抛物线的位置关系.
【分析】(1)设出A、B坐标,利用斜率公式及直线PA与PB的倾斜角互补两直线斜率相反,从而求出AB斜率.
(2)若PA⊥PB,则两直线斜率积为﹣1,求出直线AB 的方程,可得直线AB经过定点(﹣2,5).
【解答】证明:(1)设点A(x1, ),B(x2,
),B(x2, ),
),
若直线PA与PB的倾斜角互补,则两直线斜率相反,
又kPA= =
=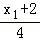 ,kPB=
,kPB=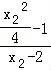 =
=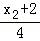 ,
,
所以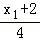 +
+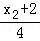 =0,
=0,
整理得x1+x2+4=0,
所以kAB=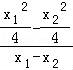 =
=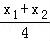 =﹣1.
=﹣1.
(2)解:因为PA⊥PB,
所以kPAkPB=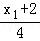 •
•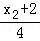 =﹣1,
=﹣1,
即x1x2+2(x1+x2)+20=0,①
直线AB的方程为: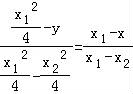 ,
,
整理得:4y﹣ =(x1+x2)(x﹣x1),
=(x1+x2)(x﹣x1),
即x1x2﹣x(x1+x2)+4y=0,②
由①②可得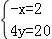 ,
,
解得 ,
,
即直线AB经过定点(﹣2,5).
设函数f(x)=(x+2a)ln(x+1)﹣2x,a∈R.
(1)当a=1时,求函数f(x)的单调区间及所有零点;
(2)设A(x1,y1),B(x2,y2),C(x3,y3)为函数g(x)=f(x)+x2﹣xln(x+1)图象上的三个不同点,且x1+x2=2x3.问:是否存在实数a,使得函数g(x)在点C处的切线与直线AB平行?若存在,求出所有满足条件的实数a的值;若不存在,请说明理由.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;利用导数研究函数的极值.
【分析】(1)求出函数的导数,根据函数的单调性判断函数的零点即可;
(2)求出g(x)的表达式,根据直线AB的斜率k=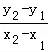 ,得到g′(
,得到g′(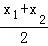 )=
)=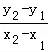 ,即aln
,即aln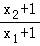 =
=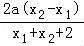 ,通过讨论a=0和a≠0,从而确定满足题意的a的值即可.
,通过讨论a=0和a≠0,从而确定满足题意的a的值即可.
【解答】解:(1)当a=1时,f(x)=(x+2)ln(x+1)﹣2x,
则f′(x)=ln(x+1)+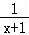 ﹣1,
﹣1,
记h(x)=ln(x+1)+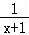 ﹣1,
﹣1,
则h′(x)= ≥0,即x≥0,
≥0,即x≥0,
从而,h(x)在(0,+∞)上单调递增,在(﹣1,0)上单调递减,
则h(x)≥h(0)=0,即f′(x)≥0恒成立,
故f(x)在(﹣1,+∞)上单调递增,无单调递减区间,
又f(0)=0,则0为唯一零点.
(2)由题意知g(x)=f(x)+x2﹣ln(x+1)=2aln(x+1)+x2﹣2x,
则g′(x)= +2x﹣2,
+2x﹣2,
直线AB的斜率k=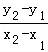 ,则有:g′(
,则有:g′(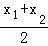 )=
)=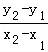 ,
,
即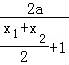 +2•
+2•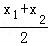 ﹣2=
﹣2=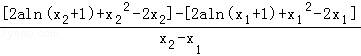 ,
,
即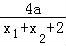 +x1+x2﹣2=
+x1+x2﹣2=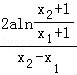 +x2+x1﹣2,
+x2+x1﹣2,
即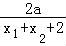 =
=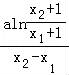 ,即aln
,即aln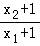 =
= ,①
,①
当a=0时,①式恒成立,满足条件;
当a≠0时,①式得ln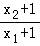 =2•
=2•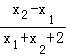 =2•
=2•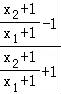 ,②
,②
记t=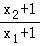 ﹣1,不妨设x2>x1,则t>0,②式得ln(t+1)=
﹣1,不妨设x2>x1,则t>0,②式得ln(t+1)=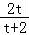 .③
.③
由(1)问可知,方程③在(0,+∞)上无零点.
综上,满足条件的实数a=0.
如图,点P是△ABC外接圆圆O在C处的切线与割线AB的交点.
(1)若∠ACB=∠APC,求证:BC是圆O的直径;
(2)若D是圆O上一点,∠BPC=∠DAC,AC= ,AB=2
,AB=2 ,PC=4,求CD的长.
,PC=4,求CD的长.

知识点:1.几何证明选讲
【考点】与圆有关的比例线段.
【分析】(1)利用PC是圆O的切线,通过∠ACP=∠ABC,得到∠APC=∠BAC,求出∠BAC=90°,说明BC是圆O的直径.
(2)说明△APC∽△CAD,推出 ,利用数据关系求解即可.
,利用数据关系求解即可.
【解答】(1)证明:∵PC是圆O的切线,∴∠ACP=∠ABC,
又∵∠ACB=∠APC,∴∠APC=∠BAC,
而∠PAC+∠BAC=180°,
∴∠BAC=90°,∴BC是圆O的直径.
(2)解:∵∠BPC=∠DAC,∠ACP=∠ADC,
∴△APC∽△CAD,∴ ,∴AC2=PA•CD,①
,∴AC2=PA•CD,①
又由切割线定理PC2=PA•PB,PC=4,AB=2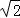 ,
,
得PA=2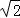 ,②
,②
由①②得CD=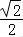 .
.
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 .
.
(1)写出曲线C的直角坐标方程;
(2)已知直线l与x轴的交点为P,与曲线C的交点为A,B,若AB的中点为D,求|PD|的长.
知识点:2.坐标系与参数方程
【考点】简单曲线的极坐标方程;参数方程化成普通方程.
【分析】(1)曲线C的极坐标方程化为 ,由此能求出曲线C的直角坐标方.
,由此能求出曲线C的直角坐标方.
(2)P的坐标为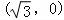 ,将l的参数方程代入曲线C的直角坐标方程得:
,将l的参数方程代入曲线C的直角坐标方程得: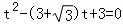 ,由此能求出|PD|的长.
,由此能求出|PD|的长.
【解答】解:(1)∵曲线C的极坐标方程为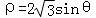 ,
,
∴ ,
,
∴x2+y2=2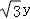 ,
,
∴曲线C的直角坐标方程为 .
.
(2)P的坐标为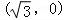 ,在平面直角坐标系xOy中,直线l的参数方程为
,在平面直角坐标系xOy中,直线l的参数方程为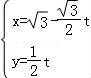 (t为参数),
(t为参数),
将l的参数方程代入曲线C的直角坐标方程得: ,
,
设点A,B,D对应的参数分别为t1,t2,t3,
则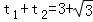 ,t1t2=3,
,t1t2=3,
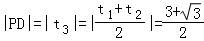 ,
,
∴|PD|的长为 .
.
若关于x的不等式|x+a|≤b的解集为[﹣6,2].
(1)求实数a,b的值;
(2)若实数m,n满足|am+n|< ,|m﹣bn|<
,|m﹣bn|< ,求证:|n|<
,求证:|n|< .
.
知识点:3.不等式选讲
【考点】绝对值不等式的解法.
【分析】(1)关于x的不等式|x+a|≤b的解集为[﹣b﹣a,b﹣a],利用条件建立方程组,即可求实数a,b的值;
(2)利用|n|=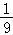 |(2m+n)﹣(2m﹣8n)|≤
|(2m+n)﹣(2m﹣8n)|≤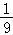 |2m+n|+2|m﹣4n|,即可证明结论.
|2m+n|+2|m﹣4n|,即可证明结论.
【解答】(1)解:关于x的不等式|x+a|≤b的解集为[﹣b﹣a,b﹣a],
∵关于x的不等式|x+a|≤b的解集为[﹣6,2],
∴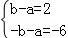 ,∴a=2,b=4;
,∴a=2,b=4;
(2)证明:∵实数m,n满足|am+n|< ,|m﹣bn|<
,|m﹣bn|<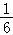 ,
,
∴|n|= |(2m+n)﹣(2m﹣8n)|≤
|(2m+n)﹣(2m﹣8n)|≤ |2m+n|+2|m﹣4n|<
|2m+n|+2|m﹣4n|<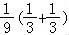 =
=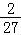 .
.