已知全集U={1,2,3,4,5,6,7,8},A={2,5,8},B={1,3,5,7},则(∁UA)∩B等于( )
A.{5} B.{1,3,7}
C.{2,8} D.{1,3,4,5,6,7,8}
知识点:3.集合的基本运算
B
【考点】交、并、补集的混合运算.
【专题】计算题.
【分析】利用补集的定义求出CUA;再利用交集的定义求出(∁UA)∩B.
【解答】解:∵U={1,2,3,4,5,6,7,8},A={2,5,8},
∴CUA={1,3,4,6,7}
∵B={1,3,5,7},
∴(∁UA)∩B={1,3,7}
故选B
【点评】本题考查利用集合的交集、补集、并集的定义进行交、并、补的混合运算.
函数 的定义域是( )
的定义域是( )
A.{x|x>6} B.{x|﹣3<x<6} C.{x|x>﹣3} D.{x|﹣3≤x<6}
知识点:2.定义域与值域
D
【考点】对数函数的定义域;函数的定义域及其求法.
【专题】计算题.
【分析】要使函数有意义,必须使函数的每一部分都有意义,函数定义域是各部分定义域的交集.
【解答】解:要使函数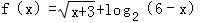 有意义,x+3≥0,且6﹣x>0
有意义,x+3≥0,且6﹣x>0
∴|﹣3≤x<6
∴函数的定义域为:{x|﹣3≤x<6}
故答案选D.
【点评】函数定义域是各部分定义域的交集.
已知p:2+2=5,q:3≥2,则下列判断中,错误的是( )
A.p或q为真,非q为假 B.p或q为真,非p为真
C.p且q为假,非p为假 D.p且q为假,p或q为真
知识点:6.简单的逻辑联结词
C
【考点】复合命题的真假.
【专题】简易逻辑.
【分析】对于命题p:2+2=5,是假命题;对于q:3≥2,是真命题.利用复合命题的真假判定方法即可判断出.
【解答】解:对于命题p:2+2=5,是假命题;
对于q:3≥2,是真命题.
∴p∨q为真命题,p∧q是假命题,¬p为真命题,¬q为假命题.
∴C是假命题.
故选:C.
【点评】本题考查了简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
下列函数中,既是偶函数又在(﹣∞,0)上单调递增的是( )
A.y=x3 B.y=cosx C.y=ln|x| D.y=
知识点:3.单调性与最大(小)值
D
【考点】奇偶性与单调性的综合.
【专题】函数的性质及应用.
【分析】分别判断函数的奇偶性和单调性即可.
【解答】解:A.y=x3在(﹣∞,0)上单调递增,为奇函数.不满足条件.
B.y=cosx在(﹣∞,0)上不单调,为偶函数.不满足条件.
C.y=ln|x|=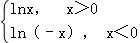 在(﹣∞,0)上单调递减,为偶函数.不满足条件.
在(﹣∞,0)上单调递减,为偶函数.不满足条件.
D.y=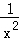 在(﹣∞,0)上单调递增,为偶函数,满足条件.
在(﹣∞,0)上单调递增,为偶函数,满足条件.
故选:D.
【点评】本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性.
对命题“∃x0∈R,x02﹣2x0+4≤0”的否定正确的是( )
A.∃x0∈R,x02﹣2x0+4>0 B.∀x∈R,x2﹣2x+4≤0
C.∀x∈R,x2﹣2x+4>0 D.∀x∈R,x2﹣2x+4≥0
知识点:7.全称量词与存在量词
C
【考点】特称命题;命题的否定.
【专题】常规题型.
【分析】通过特称命题的否定是全称命题,直接判断选项即可.
【解答】解:因为命题“∃x0∈R,x02﹣2x0+4≤0”的否定是“∀x∈R,x2﹣2x+4>0”.
故选C.
【点评】本题考查命题的否定的判断,注意全称命题与特称命题互为否命题.
为了得到函数 的图象,可以把函数
的图象,可以把函数 的图象( )
的图象( )
A.向左平移3个单位长度 B.向右平移3个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
知识点:8.指数函数及其性质
D
【考点】指数函数的图像变换.
【专题】转化思想.
【分析】将题目中:“函数 ”的式子化成
”的式子化成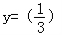 (x﹣1),对照与函数
(x﹣1),对照与函数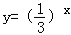 的关系即可得.
的关系即可得.
【解答】解:∵函数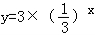 化成:
化成: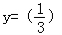 (x﹣1),∴可以把函数
(x﹣1),∴可以把函数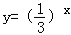 的图象向右平移1个单位长度得到函数
的图象向右平移1个单位长度得到函数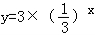 的图象.
的图象.
故选D.
【点评】本题主要考查指数运算以函数图象的平移规律,图形的平移只改变图形的位置,而不改变图形的形状和大小.
如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )

A.在区间(﹣2,1)上f(x)是增函数 B.在(1,3)上f(x)是减函数
C.在(4,5)上f(x)是增函数 D.当x=4时,f(x)取极大值
知识点:3.导数在研究函数中的应用
C
【考点】导数的几何意义;利用导数研究函数的单调性.
【专题】计算题.
【分析】由于f′(x)≥0⇒函数f(x)d单调递增;f′(x)≤0⇒单调f(x)单调递减,观察f′(x)的图象可知,通过观察f′(x)的符号判定函数的单调性即可
【解答】解:由于f′(x)≥0⇒函数f(x)d单调递增;f′(x)≤0⇒单调f(x)单调递减
观察f′(x)的图象可知,
当x∈(﹣2,1)时,函数先递减,后递增,故A错误
当x∈(1,3)时,函数先增后减,故B错误
当x∈(4,5)时函数递增,故C正确
由函数的图象可知函数在4处取得函数的极小值,故D错误
故选:C
【点评】本题主要考查了导数的应用:通过导数的符号判定函数单调性,要注意不能直接看导函数的单调性,而是通过导函数的正负判定原函数的单调性
曲线y=4x﹣x3在点(﹣1,﹣3)处的切线方程是( )
A.y=7x+4 B.y=7x+2 C.y=x﹣4 D.y=x﹣2
知识点:1.变化率与导数
D
【考点】导数的几何意义.
【分析】已知点(﹣1,﹣3)在曲线上,若求切线方程,只需求出曲线在此点处的斜率,利用点斜式求出切线方程.
【解答】解:∵y=4x﹣x3,
∴y'︳x=﹣1=4﹣3x2︳x=﹣1=1,
∴曲线在点(﹣1,﹣3)处的切线的斜率为k=1,
即利用点斜式求出切线方程是y=x﹣2,
故选D.
【点评】本题属于求过曲线上点的切线方程的基础题,只要利用导数的几何意义,求出该切线的斜率即可.
已知定义域为R的函数f(x)在区间(4,+∞)上为减函数,且函数y=f(x+4)为偶函数,则( )
A.f(2)>f(3) B.f(2)>f(5) C.f(3)>f(5) D.f(3)>f(6)
知识点:3.单调性与最大(小)值
D
【考点】奇偶性与单调性的综合;函数的图象与图象变化.
【专题】转化思想.
【分析】先利用函数的奇偶性求出f(2)=f(6),f(3)=f(5),再利用单调性判断函数值的大小.
【解答】解:∵y=f(x+4)为偶函数,∴f(﹣x+4)=f(x+4)
令x=2,得f(2)=f(﹣2+4)=f(2+4)=f(6),
同理,f(3)=f(5),又知f(x)在(4,+∞)上为减函数,
∵5<6,∴f(5)>f(6);∴f(2)<f(3);f(2)=f(6)<f(5)
f(3)=f(5)>f(6).
故选D
【点评】此题主要考查偶函数的图象性质:关于y轴对称及函数的图象中平移变换.
用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x,x+2,10﹣x}(x≥0),则f(x)的最大值为( )
A.4 B.5 C.6 D.7
知识点:3.单调性与最大(小)值
C
【考点】函数的最值及其几何意义.
【专题】计算题.
【分析】在同一坐标系内画出三个函数y=10﹣x,y=x+2,y=2x的图象,以此作出函数f(x)图象,观察最大值的位置,通过求函数值,解出最大值.
【解答】解:10﹣x是减函数,x+2是增函数,2x是增函数,令x+2=10﹣x,x=4,此时,x+2=10﹣x=6,如图:
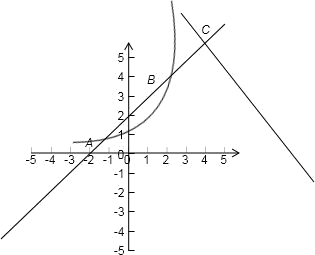
y=x+2 与y=2x交点是A、B,y=x+2与 y=10﹣x的交点为C(4,6),
由上图可知f(x)的图象如下:
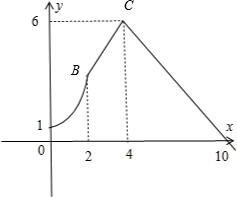
C为最高点,而C(4,6),所以最大值为6.
故选:C
【点评】本题考查了函数的概念、图象、最值问题.利用了数形结合的方法.关键是通过题意得出f(x)的简图.
已知函数f(x)= ,若f(2﹣x2)>f(x),则实数x的取值范围是( )
,若f(2﹣x2)>f(x),则实数x的取值范围是( )
A.(﹣∞,﹣1)∪(2,+∞) B.(﹣∞,﹣2)∪(1,+∞) C.(﹣2,1) D.(﹣1,2)
知识点:12.绝对值函数与分段函数及其他函数
C
【考点】分段函数的应用.
【专题】函数的性质及应用.
【分析】根据分段函数的表达式,判断函数的单调性,即可得到结论.
【解答】解:当x≤0时,f(x)=x≤0,且函数单调递增,
当x>0时,f(x)=ln(x+1)>0,且函数单调递增,
故函数在R上为增函数,
则不等式f(2﹣x2)>f(x),
等价为2﹣x2>x,
即x2+x﹣2<0,
解得﹣2<x<1,
故实数x的取值范围是(﹣2,1),
故选:C
【点评】本题主要考查不等式的求解,根据分段函数的表达式,判断函数的单调性是解决本题的关键.
已知tan(α+β)= ,tan(α+
,tan(α+ )=
)= ,则tan(β﹣
,则tan(β﹣ )= .
)= .
知识点:4.和角公式与倍(半)角公式
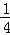
【考点】两角和与差的正切函数.
【专题】三角函数的求值.
【分析】由三角函数的公式可得tan(β﹣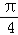 )=tan=
)=tan=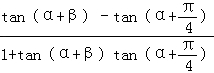 ,代入已知数据化简可得.
,代入已知数据化简可得.
【解答】解:∵tan(α+β)=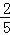 ,tan(α+
,tan(α+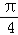 )=
)=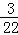 ,
,
∴tan(β﹣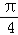 )
)
=tan
=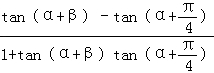
=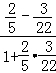 =
=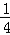 ,
,
故答案为: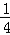 .
.
【点评】本题考查两角差的正切公式,角的整体代入是解决问题的关键,属基础题.
函数 的导数为 .
的导数为 .
知识点:2.导数的计算
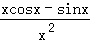
【考点】导数的运算.
【分析】根据导数的运算法则可得答案.
【解答】解:∵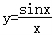 ∴y'=
∴y'=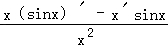 =
=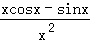
故答案为: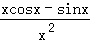
【点评】本题主要考查导数的运算法则.属基础题.求导公式一定要熟练掌握.
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1﹣x),则 = .
= .
知识点:5.奇偶性与周期性
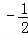
【考点】函数的周期性;函数奇偶性的性质;函数的值.
【专题】计算题.
【分析】由题意得 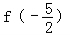 =f(﹣
=f(﹣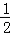 )=﹣f(
)=﹣f(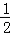 ),代入已知条件进行运算.
),代入已知条件进行运算.
【解答】解:∵f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1﹣x),
∴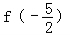 =f(﹣
=f(﹣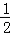 )=﹣f(
)=﹣f(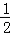 )=﹣2×
)=﹣2×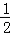 (1﹣
(1﹣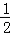 )=﹣
)=﹣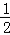 ,
,
故答案为:﹣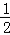 .
.
【点评】本题考查函数的周期性和奇偶性的应用,以及求函数的值.
给出四个命题:(1)若sin2A=sin2B,则△ABC为等腰三角形;(2)若sinA=cosB,则△ABC为直角三角形;(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;(4)若cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,则△ABC为正三角形,以上正确命题的是 .
知识点:9.正弦定理和余弦定理(解三角形)
(3)(4)
【考点】正弦定理.
【专题】三角函数的图像与性质;简易逻辑.
【分析】(1)由sin2A=sin2B,A,B∈(0,π),可得2A=2B,或2A+2B=π,即可判断出正误;
(2)由sinA=cosB=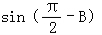 ,A,B∈(0,π),可得A=
,A,B∈(0,π),可得A=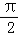 ﹣B,或A+
﹣B,或A+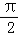 ﹣B=π,即可判断出正误;
﹣B=π,即可判断出正误;
(3)由sin2A+sin2B+sin2C<2,利用倍角公式可得: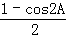 +
+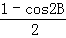 +
+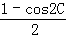 <2,化为cos2A+cos2B+cos2C>﹣1,再利用倍角公式、和差公式化为cosAcosBcosC<0,即可判断出正误;
<2,化为cos2A+cos2B+cos2C>﹣1,再利用倍角公式、和差公式化为cosAcosBcosC<0,即可判断出正误;
(4)由cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,利用余弦函数的值域,可得A﹣B=B﹣C=C﹣A=0,即可判断出正误.
【解答】解:(1)若sin2A=sin2B,∵A,B∈(0,π),∴2A=2B,或2A+2B=π,解得A=B,或A+B=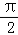 ,则△ABC为等腰三角形或直角三角形,因此不正确;
,则△ABC为等腰三角形或直角三角形,因此不正确;
(2)若sinA=cosB= ,∵A,B∈(0,π),∴A=
,∵A,B∈(0,π),∴A=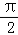 ﹣B,或A+
﹣B,或A+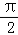 ﹣B=π,解得A+B=
﹣B=π,解得A+B=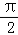 或
或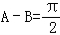 ,则△ABC为钝角三角形或直角三角形,因此不正确;
,则△ABC为钝角三角形或直角三角形,因此不正确;
(3)∵sin2A+sin2B+sin2C<2,∴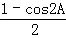 +
+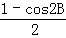 +
+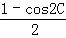 <2,化为cos2A+cos2B+cos2C>﹣1,∴2cos2A+2cos(B+C)cos(B﹣C)>0,
<2,化为cos2A+cos2B+cos2C>﹣1,∴2cos2A+2cos(B+C)cos(B﹣C)>0,
∴cosA>0,∴cosAcosBcosC<0,因此△ABC为钝角三角形,正确;
(4)若cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,∵cos(A﹣B)∈(﹣1,1],cos(B﹣C)∈(﹣1,1],cos(C﹣A)∈(﹣1,1],可知:只有三个都等于1,又A,B,C∈(0,π),∴A﹣B=B﹣C=C﹣A=0,∴A=B=C,则△ABC为正三角形,正确.
以上正确的命题是:(3)(4).
故答案为:(3)(4).
【点评】本题考查了三角函数的值域、三角形内角和定理、倍角公式与和差公式、诱导公式,考查了推理能力与计算能力,属于中档题.
如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这段时间的最大温差;
(2)写出这段时间的函数解析式.

知识点:7.函数y=Asin(wx+@)+B
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】(1)由图象的最高点与最低点易于求出这段时间的最大温差;
(2)A、b可由图象直接得出,ω由周期求得,然后通过特殊点求φ,则问题解决.
【解答】解:(1)由图示,这段时间的最大温差是30﹣10=20℃,
(2)图中从6时到14时的图象是函数y=Asin(ωx+∅)+b的半个周期,
∴ ,解得
,解得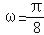 ,
,
由图示,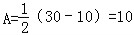 ,
,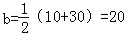 ,
,
这时, ,
,
将x=6,y=10代入上式,可取 ,
,
综上,所求的解析式为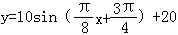 ,x∈.
,x∈.
【点评】本题主要考查由函数y=Asin(ωx+∅)+b的部分图象确定其解析式的基本方法.
已知命题p:“∀x∈,x2﹣a≥0”,命题q:“∃x0∈R,x02+2ax0+2﹣a=0”,若命题“p且q”是真命题,求实数a的取值范围.
知识点:7.全称量词与存在量词
【考点】四种命题的真假关系.
【分析】已知p且q是真命题,得到p、q都是真命题,若p为真命题,a≤x2恒成立;若q为真命题,即x2+2ax+2﹣a=0有实根,即△≥0,分别求出a的范围后,解出a的取值范围.
【解答】解:由“p且q”是真命题,则p为真命题,q也为真命题.
若p为真命题,a≤x2恒成立,
∵x∈,
∴a≤1 ①;
若q为真命题,即x2+2ax+2﹣a=0有实根,
△=4a2﹣4(2﹣a)≥0,
即a≥1或a≤﹣2 ②,
对①②求交集,可得{a|a≤﹣2或a=1},
综上所求实数a的取值范围为a≤﹣2或a=1.
【点评】本题是一道综合题,主要利用命题的真假关系,求解关于a的不等式.
某商店销售洗衣粉,年销售总量为6000包,每包进价2.8元,销售价3.4元.全年分若干次进货,每次进货均为x包.已知每次进货运输劳务费为62.5元,全年保管费为1.5x元.
(1)把该店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大化,问每次该进货多少包?
知识点:4.生活中的优化问题举例
【考点】函数最值的应用.
【专题】应用题;函数的性质及应用;不等式的解法及应用.
【分析】(1)由年销售总量为6000包,每次进货均为x包,可得进货次数,进而根据每包进价为2.8元,销售价为3.4元,计算出收入,由每次进货的运输劳务费为62.5元,全年保管费为1.5x元计算出成本,相减可得利润的表达式;
(2)由(1)中函数的解析式,由基本不等式,结合x的实际意义,可得使利润最大,每次应进货包数.
【解答】解:(1)由题意可知:一年总共需要进货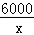 (x∈N*且x≤6000)次,
(x∈N*且x≤6000)次,
∴y=3.4×6000﹣2.8×6000﹣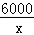 •62.5﹣1.5x,
•62.5﹣1.5x,
整理得: y=3600﹣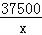 ﹣
﹣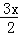 (x∈N*且x≤6000).
(x∈N*且x≤6000).
(2)y=3600﹣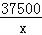 ﹣
﹣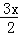 ≤3600﹣2
≤3600﹣2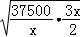 =2100
=2100
(当且仅当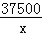 =
=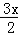 ,即x=500时取等号)
,即x=500时取等号)
∴当x=500时,ymax=3600﹣1500=2100(元),
答:当每次进货500包时,利润最大为2100元.
【点评】本题考查的知识点是函数最值的应用,其中根据已知条件计算出利润y(元)元表示为每次进货量x(包)的函数表达式是解答本题的关键.
已知函数f(x)=(x2+1)(x+a)(a∈R),当f′(﹣1)=0时,求函数y=f(x),在 上的最大值和最小值.
上的最大值和最小值.
知识点:3.导数在研究函数中的应用
【考点】利用导数求闭区间上函数的最值.
【专题】综合题.
【分析】由f(x)=x3+ax2+x+a,知f′(x)=3x2+2ax+1,故f′(﹣1)=3﹣2a+1=0,所以a=2.由此能求出函数y=f(x),在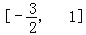 上的最大值和最小值.
上的最大值和最小值.
【解答】解:f(x)=x3+ax2+x+a,
f′(x)=3x2+2ax+1,
f′(﹣1)=3﹣2a+1=0,
∴a=2.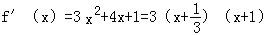 ,
,
由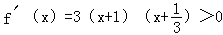 ,得x<﹣1,或x>﹣
,得x<﹣1,或x>﹣ ;
;
由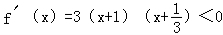 ,得
,得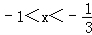 .
.
∴函数的递增区间是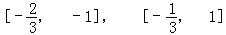 ;
;
函数的递减区间是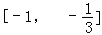 .
.
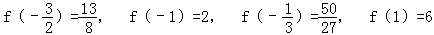 ,
,
∴函数f(x)在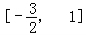 上的最大值为6,最小值
上的最大值为6,最小值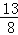 .
.
【点评】本题考查函数在闭区间上的最大值和最小值的求法,解题时要认真审题,注意导数性质的灵活运用,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
已知函数y=x3+3ax2+3bx+c在x=2处有极值,且其图象在x=1处的切线与直线6x+2y+5=0平行.
(1)求函数的单调区间;
(2)求函数的极大值与极小值的差.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的极值;利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.
【专题】函数的性质及应用;导数的综合应用.
【分析】(1)根据极值点是导函数对应方程的根,可知x=2为y′=0的根,结合导数的几何意义有k=y′|x=1,列出关于a,b的方程组,求解可得到y的解析式,令y′>0和y′<0,即可求得函数的单调区间;
(2)根据(1)可得y′=0的根,再结合单调性,即可得到函数的极大值与极小值,从而求得答案.
【解答】解:(1)∵函数y=x3+3ax2+3bx+c,
∴y'=3x2+6ax+3b,
∵函数y=x3+3ax2+3bx+c在x=2处有极值,
∴当x=2时,y′=0,即12+12a+3b=0,①
∵函数图象在x=1处的切线与直线6x+2y+5=0平行,
∴k=y′|x=1=3+6a+3b=﹣3,②
联立①②,解得a=﹣1,b=0,
∴y=x3﹣3x2+c,则y'=3x2﹣6x,
令y'=3x2﹣6x>0,解得x<0或x>2,
令y'=3x2﹣6x<0,解得0<x<2,
∴函数的单调递增区间是(﹣∞,0),(2,+∞),单调递减区间是(0,2);
(2)由(1)可知,y'=3x2﹣6x,
令y′=0,即3x2﹣6x=0,解得x=0,x=2,
∵函数在(﹣∞,0)上单调递增,在(0,2)上单调递减,在(2,+∞)上单调递增,
∴函数在x=0时取得极大值c,在x=2时取得极小值c﹣4,
∴函数的极大值与极小值的差为c﹣(c﹣4)=4.
【点评】本题考查了导数的几何意义,导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.考查了利用导数研究函数的单调性,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.考查了利用导数研究函数的极值,求函数极值的步骤是:先求导函数,令导函数等于0,求出方程的根,确定函数在方程的根左右的单调性,根据极值的定义,确定极值点和极值.
已知函数f(x)=ex﹣ln(x+m)
(Ι)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明f(x)>0.
知识点:3.导数在研究函数中的应用
【考点】利用导数研究函数的单调性;根据实际问题选择函数类型.
【专题】压轴题;导数的综合应用.
【分析】(Ⅰ)求出原函数的导函数,因为x=0是函数f(x)的极值点,由极值点处的导数等于0求出m的值,代入函数解析式后再由导函数大于0和小于0求出原函数的单调区间;
(Ⅱ)证明当m≤2时,f(x)>0,转化为证明当m=2时f(x)>0.求出当m=2时函数的导函数,可知导函数在(﹣2,+∞)上为增函数,并进一步得到导函数在(﹣1,0)上有唯一零点x0,则当x=x0时函数取得最小值,借助于x0是导函数的零点证出f(x0)>0,从而结论得证.
【解答】(Ⅰ)解:∵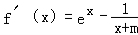 ,x=0是f(x)的极值点,∴
,x=0是f(x)的极值点,∴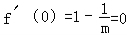 ,解得m=1.
,解得m=1.
所以函数f(x)=ex﹣ln(x+1),其定义域为(﹣1,+∞).
∵ .
.
设g(x)=ex(x+1)﹣1,则g′(x)=ex(x+1)+ex>0,所以g(x)在(﹣1,+∞)上为增函数,
又∵g(0)=0,所以当x>0时,g(x)>0,即f′(x)>0;当﹣1<x<0时,g(x)<0,f′(x)<0.
所以f(x)在(﹣1,0)上为减函数;在(0,+∞)上为增函数;
(Ⅱ)证明:当m≤2,x∈(﹣m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时f(x)>0.
当m=2时,函数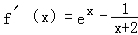 在(﹣2,+∞)上为增函数,且f′(﹣1)<0,f′(0)>0.
在(﹣2,+∞)上为增函数,且f′(﹣1)<0,f′(0)>0.
故f′(x)=0在(﹣2,+∞)上有唯一实数根x0,且x0∈(﹣1,0).
当x∈(﹣2,x0)时,f′(x)<0,当x∈(x0,+∞)时,f′(x)>0,
从而当x=x0时,f(x)取得最小值.
由f′(x0)=0,得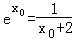 ,ln(x0+2)=﹣x0.
,ln(x0+2)=﹣x0.
故f(x)≥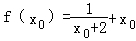 =
=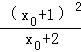 >0.
>0.
综上,当m≤2时,f(x)>0.
【点评】本题考查了利用导数研究函数的单调性,利用导数求函数在闭区间上的最值,考查了不等式的证明,考查了函数与方程思想,分类讨论的数学思想,综合考查了学生分析问题和解决问题的能力.熟练函数与导数的基础知识是解决该题的关键,是难题.