已知空间直角坐标系中A(1,1,0)且 AB=(4,0,2),则B点坐标为( )
AB=(4,0,2),则B点坐标为( )
A.(9,1,4) B.(9,﹣1,﹣4) C.(8,﹣1,﹣4) D.(8,1,4)
知识点:7.空间直角坐标系
A
【考点】共线向量与共面向量;空间中的点的坐标.
【专题】计算题.
【分析】设出B的坐标,利用向量关系,即可得到结论.
【解答】解:设B(x,y,z)
∵空间直角坐标系中A(1,1,0)且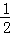
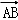 =(4,0,2),
=(4,0,2),
所以(x﹣1,y﹣1,z)=(8,0,4)
所以x=9,y=1,z=4,
B点坐标为(9,1,4)
故选A.
【点评】本题考查空间向量的平行与相等,考查学生的计算能力,属于基础题.
正四棱锥S﹣ABCD的底面边长为 ,高SE=8,则过点A,B,C,D,S的球的半径为( )
,高SE=8,则过点A,B,C,D,S的球的半径为( )
A.3 B.4 C.5 D.6
知识点:11.球
C
【考点】球内接多面体;球的体积和表面积.
【专题】空间位置关系与距离.
【分析】先画出图形,正四棱锥外接球的球心在它的底面的中心,然后根据勾股定理列方程,解出球的半径即可.
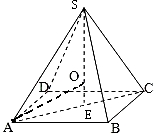
【解答】解:如图,设正四棱锥底面的中心为E,过点A,B,C,D,S的球的球心为O,半径为R,则
在直角三角形AEO中,AO=R,AE=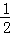 BD=4,OE=SE﹣AO=8﹣R
BD=4,OE=SE﹣AO=8﹣R
由AO2=AE2+OE2得R2=42+(8﹣R)2,解得R=5
球半径R=5,
故选C.
【点评】本题主要考查球,球的内接体问题,考查计算能力和空间想象能力,属于中档题.
已知过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,且与直线ax﹣y+1=0垂直,则a=( )
A. B.1 C.2 D.
B.1 C.2 D.
知识点:4.直线与圆的位置关系
C
【考点】直线与圆的位置关系;直线的一般式方程与直线的垂直关系.
【专题】直线与圆.
【分析】由题意判断点在圆上,求出P与圆心连线的斜率就是直线ax﹣y+1=0的斜率,然后求出a的值即可.
【解答】解:因为点P(2,2)满足圆(x﹣1)2+y2=5的方程,所以P在圆上,
又过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,且与直线ax﹣y+1=0垂直,
所以切点与圆心连线与直线ax﹣y+1=0平行,
所以直线ax﹣y+1=0的斜率为:a=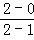 =2.
=2.
故选C.
【点评】本题考查直线与圆的位置关系,直线与直线的垂直,考查转化数学与计算能力.
已知两条不同直线m、l,两个不同平面α、β,给出下列命题:
①若l∥α,则l平行于α内的所有直线;
②若m⊂α,l⊂β且l⊥m,则α⊥β;
③若l⊂β,l⊥α,则α⊥β;
④若m⊂α,l⊂β且α∥β,则m∥l;
其中正确命题的个数为( )
A.1个 B.2个 C.3个 D.4个
知识点:4.空间点、直线、平面之间的位置关系
A
【考点】命题的真假判断与应用.
【专题】空间位置关系与距离.
【分析】由于两条不同直线m、l,两个不同平面α、β.
①若l∥α,则l与α内的直线平行或为异面直线;
②若m⊂α,l⊂β且l⊥m,则α⊥β不一定成立;
③由面面垂直的判定定理可知正确;
④若m⊂α,l⊂β且α∥β,则m∥l或为异面直线.
【解答】解:两条不同直线m、l,两个不同平面α、β.
①若l∥α,则l与α内的直线平行或为异面直线,因此不正确;
②若m⊂α,l⊂β且l⊥m,则α⊥β不一定成立;
③若l⊂β,l⊥α,则α⊥β,由面面垂直的判定定理可知正确;
④若m⊂α,l⊂β且α∥β,则m∥l或为异面直线,因此不正确.
其中正确命题的个数为1.
故选:A.
【点评】本题考查了线面、面面平行于垂直的位置关系,考查了推理能力和空间想象能力,属于基础题.
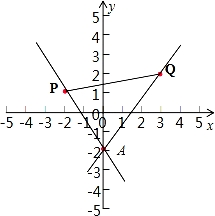
已知直线ax+y+2=0及两点P(﹣2,1)、Q(3,2),若直线与线段PQ相交,则a的取值范围是( )
A.a≤﹣ 或a≥
或a≥ B.a≤﹣
B.a≤﹣ 或a≥
或a≥ C.﹣
C.﹣ ≤a≤
≤a≤ D.﹣
D.﹣ ≤a≤
≤a≤
知识点:2.直线的交点坐标与距离公式
B
【考点】恒过定点的直线;两条直线的交点坐标.
【专题】计算题;数形结合.
【分析】确定直线系恒过的定点,画出图形,即可利用直线的斜率求出a的范围.
【解答】解:因为直线ax+y+2=0恒过(0,﹣2)点,由题意如图,
可知直线ax+y+2=0及两点P(﹣2,1)、Q(3,2),直线与线段PQ相交,
KAP=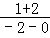 =﹣
=﹣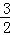 ,KAQ=
,KAQ= =
=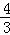 ,所以﹣a≤﹣
,所以﹣a≤﹣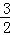 或﹣a≥
或﹣a≥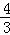 ,
,
所以a≤﹣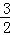 或a≥
或a≥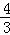
故选B.
【点评】本题考查恒过定点的直线系方程的应用,直线与直线的位置关系,考查数形结合与计算能力.
下列说法正确的有( )个
①“ ”是“θ=30°”的充分不必要条件
”是“θ=30°”的充分不必要条件
②若命题p:∃x∈R,x2﹣x+1=0,则¬p:∀x∈R,x2﹣x+1≠0
③命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
④已知a,b∈R+,若log3a>log3b,则 .
.
A.0 B.1 C.2 D.3
知识点:7.全称量词与存在量词
D
【考点】命题的真假判断与应用.
【专题】阅读型.
【分析】对于①,由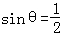 ,不一定有θ=30°.由θ=30°,一定有
,不一定有θ=30°.由θ=30°,一定有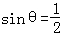 ,然后由充分条件与必要条件的定义判断;
,然后由充分条件与必要条件的定义判断;
对于②,命题p是特称命题,其否定是全程命题,注意格式的书写;
对于③,把原命题的条件和结论分别取否定即可得到其否命题,由此可判断给出的否命题是否正确;
对于④,由对数函数的性质得到a与b的大小,进一步由指数函数的性质得到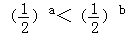 .
.
由以上分析可得答案.
【解答】解:由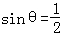 ,得:θ=30°+k360°或θ=150°+k360°(k∈Z),反之,由θ=30°,一定有
,得:θ=30°+k360°或θ=150°+k360°(k∈Z),反之,由θ=30°,一定有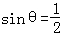 ,
,
∴“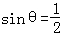 ”是“θ=30°”的必要不充分条件,命题①错误;
”是“θ=30°”的必要不充分条件,命题①错误;
命题p:∃x∈R,x2﹣x+1=0的否定为¬p:∀x∈R,x2﹣x+1≠0,∴命题②正确;
命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,∴命题③正确;
已知a,b∈R+,若log3a>log3b,则a>b,∴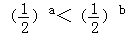 ,∴命题④正确.
,∴命题④正确.
所以正确的命题是②③④.
故选D.
【点评】本题考查了命题的真假判断与应用,考查了充分条件与必要条件的判断方法,考查了命题的否命题与命题的否定,特别是全程命题和特称命题的否定一定要注意格式的书写,
全程命题p:∀x∈M,p(x),它的否定¬p:∃x∈M,¬p(x).
特称命题p:∃x∈M,p(x),它的否定¬p:∀x∈M,¬p(x).
此题是基础题.
已知直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离等于( )
A. B.
B. C.
C. D.1
D.1
知识点:10.空间角与距离
C
【考点】点、线、面间的距离计算.
【专题】计算题;作图题;转化思想.
【分析】画出图形,由题意通过等体积法,求出三棱锥的体积,然后求出D到平面ABC的距离.
【解答】解:由题意画出图形如图:
直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,
若AB=2,AC=BD=1,则D到平面ABC的距离转化为三棱锥D﹣ABC的高为h,
所以AD=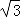 ,CD=
,CD= ,BC=
,BC=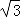
由VB﹣ACD=VD﹣ABC可知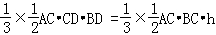
所以,h=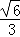
故选C.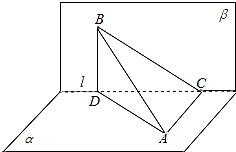
【点评】本题是基础题,考查点到平面的距离,考查转化思想的应用,等体积法是求解点到平面距离的基本方法之一,考查计算能力.
设A: ,若B是A成立的必要不充分条件,则m的取值范围是( )
,若B是A成立的必要不充分条件,则m的取值范围是( )
A.m<l B.m≤1 C.m≥1 D.m>1
知识点:5.充分条件与必要条件
D
【考点】必要条件、充分条件与充要条件的判断.
【专题】计算题.
【分析】先化简集合A,利用B是A成立的必要不充分条件,可得A⊆B,从而可求m的取值范围.
【解答】解:集合A可化为A=(0,1),集合B=(0,m)
∵B是A成立的必要不充分条件
∴(0,1)⊆(0,m)
∴m>1
故选D.
【点评】本题以集合为载体,考查四种条件,考查集合的包含关系,利用B是A成立的必要不充分条件,得A⊆B是解题的关键.
把边长为1的正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,形成三棱锥C﹣ABD的正视图与俯视图如图所示,则侧视图的面积为( )

A. B.
B. C.
C. D.
D.
知识点:2.空间几何体的三视图和直观图
B
【考点】简单空间图形的三视图.
【专题】计算题;空间位置关系与距离.
【分析】根据三棱锥的正视图和俯视图确定三棱锥的侧视图,根据侧视图的结构计算面积即可.
【解答】解:取BD的中点E,连结CE,AE,
∵平面ABD⊥平面CBD,
∴CE⊥AE,
∴三角形直角△CEA是三棱锥的侧视图,
∵BD=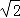 ,∴CE=AE=
,∴CE=AE=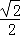 ,
,
∴△CEA的面积S=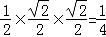 ,
,
故选:B.
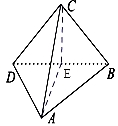
【点评】本题主要考查三视图的识别和应用,根据三棱锥的结构得到三棱锥的侧视图是解决本题的关键.
下面说法正确的是( )
A.命题“∃x∈R,使得x2+x+1≥0”的否定是“∀x∈R,使得x2+x+1≥0”
B.实数x>y是 成立的充要条件
成立的充要条件
C.设p、q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题
D.命题“若x2﹣3x+2=0则x=1”的逆否命题为假命题
知识点:5.充分条件与必要条件
D
【考点】特称命题;复合命题的真假.
【专题】阅读型.
【分析】对于A,命题“∃x∈R,使得x2+x+1≥0”的否定应是“∀x∈R,使得x2+x+1<0”,
对于B,取特例 当x=1,y=﹣1时判断为错误.
对于C,判断出p,q真假后,再判断¬p∧¬q真假.
对于D,命题“若x2﹣3x+2=0则x=1”的真假性与其逆否命题真假性相同.
【解答】解:A 命题“∃x∈R,使得x2+x+1≥0”的否定应是“∀x∈R,使得x2+x+1<0”,A错.
B 当x=1,y=﹣1时,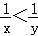 不成立. B错.
不成立. B错.
C 若“p∨q”为假命题,即p,q均为假命题,¬p,¬q均为真命题,“¬p∧¬q”也为真命题. C错.
D 若x2﹣3x+2=0,则x=1或者x=2.所以命题“若x2﹣3x+2=0则x=1”为假命题,其逆否命题也为假命题. D正确.
故选D
【点评】本题考查四种命题,命题的真假判断.属于基础题.
已知命题p:“对∀x∈R,∃m∈R,使4x+m•2x+1=0”.若命题¬p是假命题,则实数m的取值范围是( )
A.﹣2≤m≤2 B.m≥2 C.m≤﹣2 D.m≤﹣2或m≥2
知识点:6.简单的逻辑联结词
C
【考点】命题的否定;全称命题;命题的真假判断与应用.
【专题】计算题.
【分析】命题p是真命题,利用分离m结合基本不等式求解.
【解答】解:由已知,命题¬p是假命题,则命题p是真命题,
由4x+m•2x+1=0得m=﹣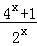 ≤﹣
≤﹣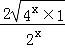 =﹣2,当且仅当x=0是取等号.
=﹣2,当且仅当x=0是取等号.
所以m的取值范围是m≤﹣2
故选C
【点评】本题考查复合命题真假的关系,参数取值范围,考查转化、逻辑推理、计算能力.
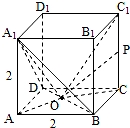
如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )

A.[ ,1] B.[
,1] B.[ ,1] C.[
,1] C.[ ,
, ] D.[
] D.[ ,1]
,1]
知识点:10.空间角与距离
B
【考点】直线与平面所成的角.
【专题】空间角.
【分析】由题意可得:直线OP于平面A1BD所成的角α的取值范围是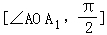 ∪
∪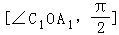 .再利用正方体的性质和直角三角形的边角关系即可得出.
.再利用正方体的性质和直角三角形的边角关系即可得出.
【解答】解:由题意可得:直线OP于平面A1BD所成的角α的取值范围是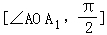 ∪
∪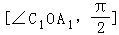 .
.
不妨取AB=2.
在Rt△AOA1中,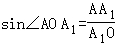 =
=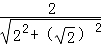 =
=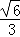 .
.
sin∠C1OA1=sin(π﹣2∠AOA1)=sin2∠AOA1=2sin∠AOA1cos∠AOA1=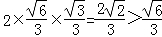 ,
,
 =1.
=1.
∴sinα的取值范围是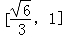 .
.
故选:B.
【点评】本题考查了正方体的性质和直角三角形的边角关系即可、线面角的求法,考查了推理能力,属于中档题.
已知空间三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),则以AB,AC为边的平行四边形的面积是 .
知识点:8.空间向量及其运算

【考点】向量在几何中的应用.
【专题】计算题.
【分析】求出向量的坐标,进而可得模长即向量的夹角,由此可计算以AB,AC为边的平行四边形的面积.
【解答】解:∵A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),
∴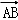 =(﹣2,﹣1,3),
=(﹣2,﹣1,3),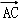 =(1,﹣3,2),|
=(1,﹣3,2),|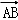 |=
|=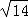 ,|
,|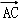 |=
|=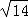
∴cos∠BAC=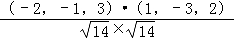 =
=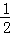 ,
,
∴∠BAC=60°…(4分)
∴S=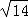 ×
×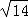 sin60°=
sin60°=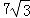
故答案为: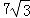
【点评】本题考查向量背景下平行四边形的面积的计算,关键是求向量的坐标及模长.
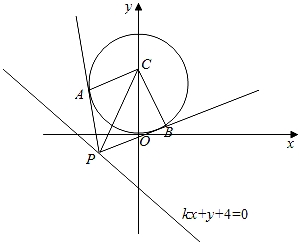
已知点p(x,y)是直线kx+y+4=0(k>0)上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 .
知识点:4.直线与圆的位置关系
2
【考点】直线与圆的位置关系;点到直线的距离公式.
【专题】计算题.
【分析】先求圆的半径,四边形PACB的最小面积是2,转化为三角形PBC的面积是1,求出切线长,再求PC的距离也就是圆心到直线的距离,可解k的值.
【解答】解:圆C:x2+y2﹣2y=0的圆心(0,1),半径是r=1,
由圆的性质知:S四边形PACB=2S△PBC,四边形PACB的最小面积是2,
∴S△PBC的最小值S=1=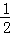 rd(d是切线长)
rd(d是切线长)
∴d最小值=2
圆心到直线的距离就是PC的最小值,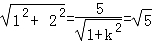
∵k>0,∴k=2
故 答案为:2
【点评】本题考查直线和圆的方程的应用,点到直线的距离公式等知识,是中档题.
已知两点A(1,2,3),B(2,1,2),P(1,1,2)点Q在直线OP上运动,则当 取得最小值时,Q点的坐标 .
取得最小值时,Q点的坐标 .
知识点:8.空间向量及其运算
【考点】空间向量的数量积运算.
【专题】计算题.
【分析】可先设Q(x,y,z),由点Q在直线OP上可得Q(λ,λ,2λ),则由向量的数量积的坐标表示可求 ,然后根据二次函数的性质可求,取得最小值时的λ,进而可求Q
,然后根据二次函数的性质可求,取得最小值时的λ,进而可求Q
【解答】解:设Q(x,y,z)
∵A(1,2,3),(2,1,2),P(1,1,2),
则由点Q在直线OP上可得存在实数λ使得 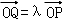 =(λ,λ,2λ)
=(λ,λ,2λ)
则Q(λ,λ,2λ)
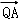 =(1﹣λ,2﹣λ,3﹣2λ),
=(1﹣λ,2﹣λ,3﹣2λ),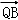 =(2﹣λ,1﹣λ,2﹣2λ)
=(2﹣λ,1﹣λ,2﹣2λ)
∴ =(1﹣λ)(2﹣λ)+(2﹣λ)(1﹣λ)+(3﹣2λ)(2﹣2λ)=2(3λ2﹣8λ+5)
=(1﹣λ)(2﹣λ)+(2﹣λ)(1﹣λ)+(3﹣2λ)(2﹣2λ)=2(3λ2﹣8λ+5)
根据二次函数的性质可得当λ=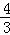 时,取得最小值﹣
时,取得最小值﹣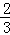 此时Q(
此时Q(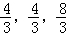 )
)
故答案为:(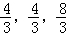 )
)
【点评】本题考查的知识点是空间向量的数量积运算,其中根据空间向量数量积的坐标运算公式,求出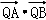 的表达式,进而将问题转化为一个二次函数最值问题,是解答本题的关键.
的表达式,进而将问题转化为一个二次函数最值问题,是解答本题的关键.
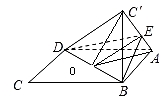
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A﹣BD﹣E与二面角E﹣BD﹣C′的大小分别为15°和30°,则 = .
= .

知识点:10.空间角与距离
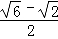
【考点】与二面角有关的立体几何综合题.
【专题】综合题;压轴题;空间位置关系与距离.
【分析】取BD的中点O,连接AO,EO,C′O,由题设知AOE=15°,∠EOC′=30°,由此利用正弦定理能求出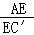 .
.
【解答】解:取BD的中点O,连接AO,EO,C′O,
∵菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,
∴C′O⊥BD,AO⊥BD,OC′=OA,
∴BD⊥平面AOC′,
∴EO⊥BD,
∵二面角A﹣BD﹣E与二面角E﹣BD﹣C′的大小分别为15°和30°,
∴∠AOE=15°,∠EOC′=30°,
∵OC′=OA,∴∠OC′E=∠OAE,
由正弦定理得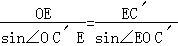 ,
,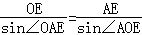 ,
,
∴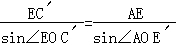 ,
,
∴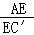 =
= =
=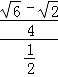 =
=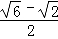 .
.
故答案为: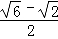 .
.
【点评】本题考查棱锥的结构特征,注意在翻折过程中哪些量发生了变化,哪些量没有发生变化;位于折线同侧的元素关系不变,位于折线两侧的元素关系会发生变化.
如图,在三棱锥P﹣ABC中,∠ABC=90°,PA⊥平面ABC,E,F分别为PB,PC的中点.
(1)求证:EF∥平面ABC;
(2)求证:平面AEF⊥平面PAB.

知识点:5.直线、平面平行的判定及其性质
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【专题】空间位置关系与距离.
【分析】(1)根据三角形中位线定理可得EF∥BC,进而根据线面平行的判定定理可得EF∥平面ABC;
(2)根据PA⊥平面ABC,可得PA⊥BC,结合∠ABC=90°,及线面垂直的判定定理可得BC⊥平面PAB,进而由线面垂直的第二判定定理可得EF平面PAB,最后由面面垂直的判定定理可得平面AEF⊥平面PAB.
【解答】证明:(1)∵E,F分别为PB,PC的中点.
∴EF∥BC,
又∵BC⊂平面ABC,EF⊄平面ABC,
∴EF∥平面ABC;
(2)∵PA⊥平面ABC,BC⊂平面ABC,
∴PA⊥BC,
又∵∠ABC=90°,
∴AB⊥BC,
又∵PA∩AB=A,PA,AB⊂平面PAB,
∴BC⊥平面PAB,
由(1)中EF∥BC,
∴EF⊥平面PAB,
又∵EF⊂平面AEF,
∴平面AEF⊥平面PAB.
【点评】本题考查的知识点是线面平行的判定定理,线面垂直的判定定理,面面垂直的判定定理,是空间线面关系的简单综合应用,难度中档.
命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立;命题q:函数f(x)=log3﹣2ax在(0,+∞)上是增函数,若p∨q为真,p∧q为假.求实数a的取值范围.
知识点:6.简单的逻辑联结词
【考点】命题的真假判断与应用.
【专题】函数的性质及应用.
【分析】根据一元二次不等式恒成立的充要条件,可求出命题p为真命题时,实数a的取值范围;根据对数函数的单调性与底数的关系,可以求出命题q为真命题时,实数a的取值范围;进而根据p∨q为真,p∧q为假,判断出p与q一真一假,由此构造关于a的不等式组,解不等式组可得实数a的取值范围.
【解答】解:若命题p为真命题,
则△=4a2﹣16<0,解得﹣2<a<2;
若命题q为真命题,
则3﹣2a>1,解得a<1
∵p∨q为真,p∧q为假.
∴p与q一真一假
即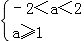 ,或
,或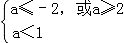
解得a≤﹣2,或1≤a<2
∴实数a的取值范围为(﹣∞,﹣2]∪[﹣1,2)
【点评】本题以命题的真假判断为载体,考查了一元二次函数的图象和性质,对数函数的图象和性质,难度不大.
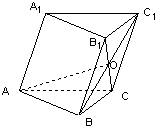
已知斜三棱柱ABC﹣A1B1C1中,∠BAC= ,∠BAA1=
,∠BAA1= ,∠CAA1=
,∠CAA1= ,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
(1)求AO的距离;
(2)求异面直线AO与BC所成的角的余弦值.

知识点:10.空间角与距离
【考点】异面直线及其所成的角;点、线、面间的距离计算.
【专题】计算题;转化思想;向量法;立体几何.
【分析】(1)设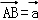 ,
,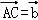 ,
,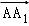 =
=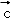 ,
,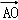 =
=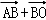 =
=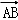 +
+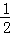 (
(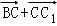 )=
)=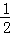 (
(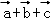 ),由此能求出AO.
),由此能求出AO.
(2)由得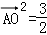 ,
, ,得
,得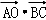 =1,|
=1,|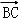 |=
|=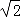 ,由此能求出异面直线AO与BC所成的角的余弦值.
,由此能求出异面直线AO与BC所成的角的余弦值.
【解答】解:(1)设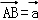 ,
,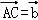 ,
,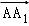 =
=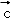 ,
,
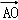 =
=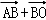 =
=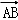 +
+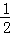 (
(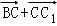 )=
)=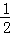 (
(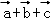 ),
),
∴AO=|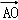 |=
|=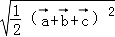 =
=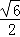 .
.
(2)由(1),得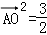 ,
, ,
,
∴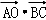 =1,|
=1,|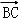 |=
|=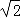 ,cos<
,cos<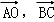 >=
>=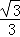 ,
,
∴异面直线AO与BC所成的角的余弦值为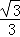 .
.
【点评】本题考查线段长的求法,考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.
已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)若M(m,n)为圆C上任意一点,求 的最大值与最小值;
的最大值与最小值;
(3)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求当|PM|最小时的点P的坐标.
知识点:4.直线与圆的位置关系
【考点】直线与圆锥曲线的综合问题.
【专题】综合题;直线与圆.
【分析】(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为﹣1;当切线过原点时,设切线方程为:y=kx,当切线的斜率为﹣1时,设切线方程为:x+y+b=0,由相切可得方程,解出即可;
(2)设k=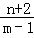 ,则k表示直线MA的斜率,其中A(1,﹣2)是定点,可知直线MA与圆有公共点,从而可得
,则k表示直线MA的斜率,其中A(1,﹣2)是定点,可知直线MA与圆有公共点,从而可得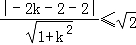 ,解出即可;
,解出即可;
(3)由两点间距离公式及切线长公式,可把|PM|=|PO|化为(x+1)2+(y﹣2)2﹣2=x2+y2,化简可得x=2y﹣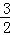 ,从而PM|=|PO|=
,从而PM|=|PO|=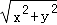 ,可化为关于y的函数,借助二次函数的性质可求;
,可化为关于y的函数,借助二次函数的性质可求;
【解答】解:圆C的方程为:(x+1)2+(y﹣2)2=2,
(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为﹣1;
当切线过原点时,设切线方程为:y=kx,相切则: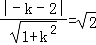 ,得
,得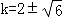 ;
;
当切线的斜率为﹣1时,设切线方程为:y+x+b=0,由相切得: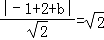 ,得b=1或b=﹣3;
,得b=1或b=﹣3;
故所求切线方程为: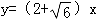 或
或 ;或x+y+1=0,或x+y﹣3=0.
;或x+y+1=0,或x+y﹣3=0.
(2)设k=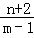 ,则k表示直线MA的斜率,其中A(1,﹣2)是定点,
,则k表示直线MA的斜率,其中A(1,﹣2)是定点,
∵M(m,n)在圆C,∴圆C与直线MA有公共点,
而直线MA的方程为:y+2=k(x﹣1),
则有:C点到直线MA的距离不大于圆C的半径即: ,解得:﹣7≤k≤﹣1,
,解得:﹣7≤k≤﹣1,
∴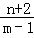 的最大值为﹣1,最小值为﹣7.
的最大值为﹣1,最小值为﹣7.
(3)由圆的切线长公式可得|PM|2=|PC|2﹣R2=(x+1)2+(y﹣2)2﹣2,
由|PM|=|PO|得,(x+1)2+(y﹣2)2﹣2=x2+y2,即2x﹣4y+3=0,即x=2y﹣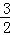 ,
,
此时|PM|=|PO|=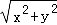 =
= =
=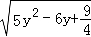 =
=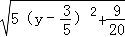 ,
,
∴当y=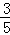 即P(
即P(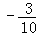 ,
,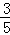 )时,|PM|最小.
)时,|PM|最小.
【点评】该题考查圆的方程、性质,考查直线与圆的位置关系,考查与圆有关的最值问题,考查转化思想.
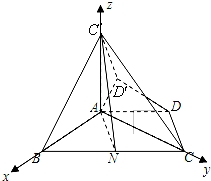
在等腰梯形ABCD中,AD∥BC,AD= BC,∠ABC=60°,N是BC的中点.将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点.将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
(Ⅰ)求证:AC⊥平面ABC′;
(Ⅱ)求证:C′N∥平面ADD′;
(Ⅲ)求二面角A﹣C′N﹣C的余弦值.

知识点:5.直线、平面平行的判定及其性质
【考点】二面角的平面角及求法;直线与平面平行的判定;直线与平面垂直的判定.
【专题】空间位置关系与距离;空间角.
【分析】(Ⅰ)由梯形的性质和N是BC的中点可得四边形ANCD是平行四边形,得到AN=DC;利用等腰梯形可得AN=AB,又∠ABC=60°,得到△ABN是等边三角形,于是AN=BN=NC,由出可得△ABC是直角三角形,即AC⊥AB,再利用面面垂直的性质即可得到结论;
(Ⅱ)由已知可得:AD∥BC,AD′∥BC′,利用面面平行的判定定理即可得出;
(Ⅲ)如图所示的空间直角坐标系,求出两个平面的法向量,利用法向量的夹角即可得到二面角的一余弦值.
【解答】(Ⅰ)证明:∵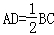 ,N是BC的中点,
,N是BC的中点,
∴AD=NC,又AD∥BC,
∴四边形ANCD是平行四边形,∴AN=DC.
又∵等腰梯形,∴AN=AB.
又∠ABC=60°,
∴△ABN是等边三角形.
∴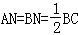 ,
,
∴△ABC是直角三角形,且∠BAC=90°.
∴AC⊥AB.
∵平面C′BA⊥平面ABC,
∴AC⊥平面ABC′.
(Ⅱ)证明:∵AD∥BC,AD′∥BC′,
AD′∩AD=A,BC∩BC′=B,
∴平面ADD′∥平面BCC′,
∴C′N∥平面ADD′.
(Ⅲ)∵AC⊥平面ABC′,
同理AC′⊥平面ABC,建立如图如示坐标系
设AB=1,
则B(1,0,0),C ,
,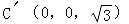 ,
,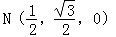 ,
,
则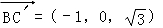 ,
,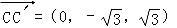 .
.
设平面C′NC的法向量为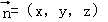 ,
,
则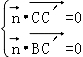 ,即
,即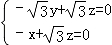 ,
,
令z=1,则x=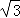 ,y=1,得
,y=1,得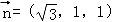 .
.
∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC.
又BD⊥AN,平面C′AN∩平面ABC=AN,
∴BD⊥平面C′AN,
设BD与AN交于点O,O则为AN的中点,O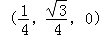 .
.
所以平面C′AN的法向量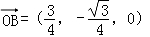 .
.
∴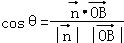 =
=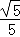 .
.
由图形可知二面角A﹣C′N﹣C为钝角.
所以二面角A﹣C′N﹣C的余弦值为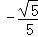 .
.
【点评】熟练掌握等腰梯形的性质、平行四边形的判定与性质、等边三角形及直角三角形的判定与性质、面面垂直与平行的判定及性质、通过建立空间直角坐标系利用法向量的夹角求空间角是解题的关键.
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是 .
.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.F,G是曲线D上不同的两点,对于定点Q(﹣3,0),有|QF|•|QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
知识点:5.曲线与方程
【考点】参数方程化成普通方程;简单曲线的极坐标方程.
【专题】方程思想;综合法;圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)设动点P的坐标为(x,y),由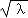 |PO|=|PA|代入坐标整理得(λ﹣1)x2+(λ﹣1)y2+6x﹣9=0,对λ分类讨论可得;
|PO|=|PA|代入坐标整理得(λ﹣1)x2+(λ﹣1)y2+6x﹣9=0,对λ分类讨论可得;
(Ⅱ)当λ=4时,曲线D的方程是x2+y2+2x﹣3=0,则由面积相等得到|QF|•|QG|sinθ=d|FG|,且圆的半径r=2,由点到直线的距离公式以及直线和圆的位置关系可得.
【解答】解:(Ⅰ)设动点P的坐标为(x,y),
则由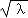 |PO|=|PA|得λ(x2+y2)=(x﹣3)2+y2,
|PO|=|PA|得λ(x2+y2)=(x﹣3)2+y2,
整理得:(λ﹣1)x2+(λ﹣1)y2+6x﹣9=0,
∵λ>0,∴当λ=1时,方程可化为:2x﹣3=0,方程表示的曲线是线段OA的垂直平分线;
当λ≠1时,则方程可化为,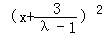 +y2=
+y2=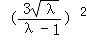 ,
,
即方程表示的曲线是以(﹣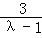 ,0)为圆心,
,0)为圆心,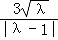 为半径的圆.
为半径的圆.
(Ⅱ)当λ=4时,曲线D的方程是x2+y2+2x﹣3=0,
故曲线D表示圆,圆心是D(﹣1,0),半径是2.
设点Q到直线FG的距离为d,∠FQG=θ,
则由面积相等得到|QF|•|QG|sinθ=d|FG|,且圆的半径r=2.
即d=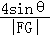 =
=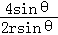 =1.于是顶点Q到动直线FG的距离为定值,
=1.于是顶点Q到动直线FG的距离为定值,
即动直线FG与定圆(x+3)2+y2=1相切.
【点评】本题考查参数方程和极坐标方程,涉及分类讨论的思想,属中档题.